பயிற்சி 4.1 (முக்கோணத்தின்கோணங்கள்)

பயிற்சி 4.1 

1. 30°, 60° மற்றும் 90° ஆகியவை ஒரு முக்கோணத்தின் கோணங்களாக அமையுமா?

தீர்வு :

30°, 60° மற்றும் 90° என்பவை கொடுக்கப்பட்ட கோணங்கள். 

கோணங்களின் கூடுதல் = 30° + 60° + 90°

 = 180° 

ஆம், கொடுக்கப்பட்ட கோணங்கள் ஒரு முக்கோணத்தின் கோணங்கள் ஆகும். 

2. 25°, 65° மற்றும் 80° ஆகிய கோணங்களைக் கொண்டு ஒரு முக்கோணத்தை அமைக்க இயலுமா?

தீர்வு : 

25°, 65° மற்றும் 80° என்பவை கொடுக்கப்பட்ட கோணங்கள் 

கோணங்களின் கூடுதல் = 25° + 65° + 80°

= 170° ≠ 180° 

இல்லை, கொடுக்கப்பட்ட கோணங்கள் ஒரு முக்கோணத்தை அமைக்காது. 

3. கீழ்க்காணும் ஒவ்வொரு முக்கோணத்திலும் x ன் மதிப்பைக் காண்க. 

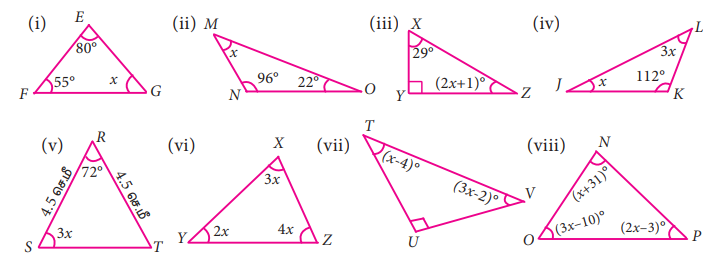
தீர்வு : 

i) ∠E = 80°, ∠F = 55°, ∠G = x 

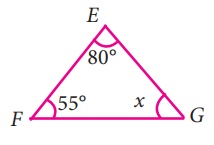
∠E + ∠F + ∠G = 180° (முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு) 

80 + 55 + x = 180 

135 + x = 180

x = 180 - 135 

x = 45° 

ii) ∠M = x, ∠N = 96°, ∠O = 22°

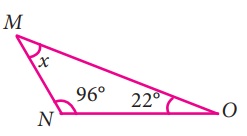
∠M + ∠N + ∠O = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)

x + 96 + 22 = 180 

x + 118 = 180

x = 180 - 118 = 62°

x = 62° 

iii) ∠X = 29°, ∠Y = 90°, ∠Z = 2x + 1°

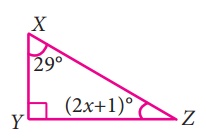
∠X + ∠Y + ∠Z = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு) 

29° + 90° + 2x+1° = 180 

120 + 2x = 180

2x = 180 - 120 = 60

x = 60 / 2

x = 30° 

iv) ∠J = x, ∠K = 112, ∠L= 3x

∠J + ∠K + ∠L = 180° 

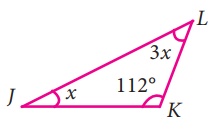
(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)

x + 112 + 3x = 180 

4x + 112 = 180

4x = 180 - 112 

x = 68

x = 68 / 4

x = 17°

v) ∠R = 72°, ∠S = 3x, ∠T = 3x

∠R + ∠S + ∠T = 180° 

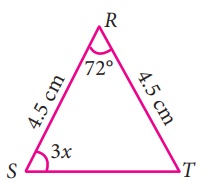
(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)

72 + 3x + 3x = 180 

6x + 72 = 180

6x = 180 - 72 = 108 

6x = 108

x = 108 / 6

x = 18°

vi) ∠X = 3x, ∠Y = 2x, ∠Z = 4x

∠X + ∠Y +∠Z = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு) 

3x + 2x + 4x = 180

9x = 180

x = 180 / 9 = 20 

x = 20° 

vii) ∠T = x + 4, ∠U = 90°, ∠V = 3x-2

∠T + ∠U + ∠V = 180° 

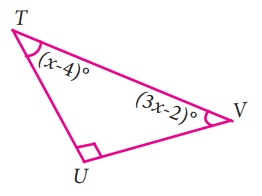
(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு) 

x - 4+ 90 + 3x - 2 = 180

4x + 84 = 180 

4x + 180 - 84

4x = 96

x = 96 / 4

x = 24° 

viii) ∠N = x + 31°, ∠O = 3x - 10, ∠P = 2x - 3

∠N + ∠O + ∠P = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு) 

x + 31 + 3x - 10 + 2x - 3 = 180

6x + 18 = 180

6x = 180 - 18 

6x = 162 

x = 162 / 6

x = 27°

4. AD, BC    என்ற இரு கோட்டுத்துண்டுகள் 0. என்ற புள்ளியில் வெட்டுகிறது   மற்றும் DC   ஐ இணைத்தால், ΔAOB மற்றும் ΔDOC படத்தில் உள்ளவாறு அமைகிறது எனில், ∠A மற்றும் ∠B ஐக் காண்க. 

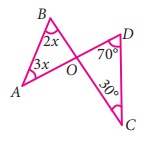
தீர்வு : 

ΔOCD, 

∠C = 30° ∠D = 70°, ∠COD = y என்க

∠C + ∠D + ∠COD = 180 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)

30+ 70 + y = 180

100 + y = 180 

y = 180 - 100

y = 80°  

∠COD = ∠BOA

(குத்தெதிர் கோணங்கள் சமம்)

ஃ ∠BOA = 80° 

∠A = 3x ∠B = 2x

∠A + ∠B + ∠BOA = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)  

3x + 2x + 80 = 180

5x = 180 - 80 

5x = 100

x = 100 / 5

x = 20°

∠A = 3x = 3 × 20 = 60

∠A = 60°

∠B = 2x = 2 × 20 = 40

∠B = 40° 

5. படத்தினை உற்றுநோக்கி, ∠A + ∠N + ∠G + ∠L + ∠E + ∠S மதிப்பைக் காண்க.

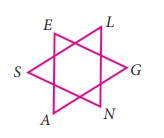
தீர்வு : 

படத்தில் 2 முக்கோணங்கள் கொடுக்கப்பட்டுள்ளது. முக்கோணத்தில் கோணங்களின் கூடுதல் 180° 

இங்கு 2 - முக்கோணங்கள்,

எனவே

ஃ ∠A + ∠N + ∠G +∠L + ∠E + ∠S = 360° 

6. ஒரு கோணத்தின் மூன்று கோணங்கள் 3 : 5 : 4 என்ற விகிதத்தில் அமைந்துள்ளன எனில், அவற்றைக் காண்க.

தீர்வு : 

கோணங்கள் 3x, 5x, 4x என்க. 

முக்கோணத்தில் கோணங்களின் கூடுதல் 180° 

3x + 5x + 4x = 180

12x = 180 

4x + 180 - 84

x = 180 / 12

x = 15°

கோணங்கள் 45°, 75°, 60°

7. ΔRST இல், ∠S ஆனது ∠R ஐ விட 10° அதிகமானது மற்றும் ∠T ஆனது ∠S ஐ விட 5° குறைவானது எனில், மூன்று கோணங்களைக் காண்க. 

தீர்வு : 

∠R = x° என்க 

∠S = x + 10°

∠T = x + 10° - 5° = x + 5° 

ஃ ∠R + ∠S + ∠T = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு) 

x + x + 10 + x + 5 = 180

3x + 15 = 180 

3x = 180 - 15 

3x = 165°

x = 165 / 3

x = 55° 

ஃ ∠R = 55°  

∠S = 55 + 10 = 65°

∠T = x + 5 = 55 + 5 = 60° 

8. ΔABC இல் ∠B ஆனது ∠A இன் 3 மடங்கு மற்றும் ∠C ஆனது ∠A இன் இருமடங்கு எனில், அக்கோணங்களைக் காண்க. 

தீர்வு : 

∠A = x என்க 

∠B = 3x 

∠C = 2x

∠A + ∠B + ∠C = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)

x + 3x + 2x = 180 

6x = 180

x = 180 / 6

x = 30° 

∠A = 30° 

∠B = 3x = 3 × 30 = 90° 

∠C = 2x = 2 × 30 = 60°

9. ΔXYZ இல் ∠X : ∠Z = 5 : 4 மற்றும் ∠Y = 72°. ∠X மற்றும் ∠Z ஐக் காண்க.

தீர்வு : 

∠X = ∠Z = 5 : 4 

∠X = 5x, ∠Z = 4x என்க

∠X + ∠Y + ∠Z = 180 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு) 

5x + 72° + 4x = 180

9x = 180 - 72 

9x = 180

x = 108 / 9

x = 12° 

ஃ ∠X = 5x = 5 × 12 = 60°

∠Z = 4x = 4 × 12 = 48° 

10. செங்கோண முக்கோணம் ABC இல் ∠B ஆனது செங்கோணம் ∠A ஆனது x + 1 மற்றும் ∠C ஆனது 2x + 5 எனில் ∠A மற்றும் ∠C ஐக் காண்க.

தீர்வு : 

∠A = x + 1, ∠B = 90°, ∠C= 2x + 5

∠A + ∠B + ∠C = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு) 

x + 1 + 90 + 2x + 5 = 180

3x + 96 = 180

3x = 180 - 96 

3x = 84

x = 84 / 3

x = 28°

ஃ ∠A = x + 1 = 28 + 1 = 29°

∠C = 2x + 5 = 2 (28) + 5 = 61°

11. செங்கோண முக்கோணம் MNO இல் ∠N = 90°, MO ஆனது P வரை நீட்டிக்கப்பட்டுள்ளது. ∠NOP = 128°, எனில், மற்ற கோணங்களைக் காண்க. 

தீர்வு : 

முக்கோணத்தின் இரு உள்கோணங்களின் கூடுதல் அவற்றின் வெளிகோணத்திற்கு சமம். 

∠M + ∠N = ∠NOP 

x + 90° = 128° 

x = 128 - 90° = 38° 

x = 38°

∠M+ ∠N + ∠O = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)

38° + 90° + y = 180

128 + y = 180

y = 180 - 128 

y = 52°

12. கொடுக்கப்பட்டுள்ள முக்கோணம் ஒவ்வொன்றிலும் x இன் மதிப்பைக் காண்க.

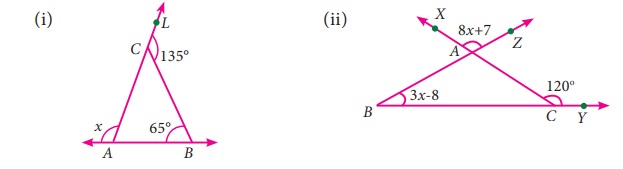
தீர்வு : 

i) ∠ACB + ∠BCL = 180°

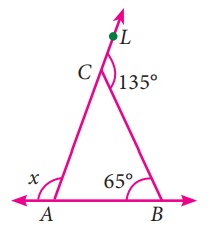
(நேர்கோட்டிலமையும் கோணங்களின் கூடுதல் பண்பு)

∠ACB + 135° = 180 

∠ACB = 180 - 135 = 45° 

முக்கோணத்தின் இரு உள்கோணங்களின் கூடுதல் அவற்றின் வெளிக் கோணத்திற்கு சமம். 

∠B + ∠C= ∠A

65° + 45° = x

x = 110° 

ii) ∠BCA + ∠ACY = 180°

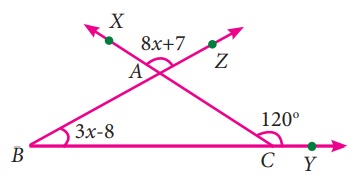
(நேர்க்கோட்டிலமையும் கோணங்களின் கூடுதல் பண்பு) 

∠BCA + 120° = 180

∠BCA = 180 - 120 

∠BCA = 60°

குத்தெதிர் கோணங்கள் சமம்

ஃ ∠XAZ = ∠BAC ⇒ ∠BAC = 8x + 7 

∠A + ∠B + C = 180° 

(முக்கோணத்தில் கோணங்களின் கூடுதல் பண்பு)

8x + 7 + 3x – 8 + 60 = 180

11x + 59 = 180 

11x = 180 - 59 = 121 

x = 121 / 11 = 11 

x = 11°

13. ΔLMN, இல் MN ஆனது O. வரை நீட்டிக்கப்பட்டுள்ளது ∠MLN = 100 - x, ∠LMN = 2x மற்றும் ∠LNO = 6x - 5, எனில் x இன் மதிப்பைக் காண்க. 

தீர்வு : 

முக்கோணத்தில் இரு உள்கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு சமம். 

∠L + ∠M = ∠LNO 

100 - x + 2x = 6x - 5 

100 + 5 = 6x - 2x + x

105 = 7x - 2x 

105 = 5x 

x = 105 / 5

x = 21° 

14. கொடுக்கப்பட்டுள்ள படத்தில் இருந்து x இன் மதிப்பைக் காண்க.

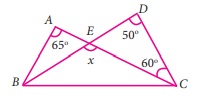
தீர்வு :

முக்கோணத்தில் இரு உள்கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு சமம் 

∠D = 50°, ∠C = 60° = ∠BEC = x

∠BCE = ∠D + ∠C 

x = 50 + 60° 

x = 110°

15. கொடுக்கப்பட்டுள்ள படத்தைப் பயன்படுத்தி x இன் மதிப்பைக் காண்க.

தீர்வு : 

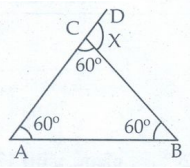
கொடுக்கப்பட்ட முக்கோணம் சமபக்க முக்கோணமாகும். 

ஃ அனைத்து கோணமும் சமம். அதாவது 60° 

முக்கோணத்தில் இரு உள் கோணங்களின் கூடுதல் அவற்றின் வெளிக்கோணத்திற்கு சமம். 

∠DCB = ∠A + ∠B

x = 60 + 60 

x = 120° 

கொள்குறி வகை வினாக்கள் 

16. ஒரு முக்கோணத்தில் மூன்று கோணங்கள் 2 : 3 : 4. என்ற விகிதத்தில் இருந்தால் அக்கோணங்கள் 

i) 20, 30, 40 

ii) 40, 60, 80 

iii) 80, 20, 80 

iv) 10, 15, 20

விடை : ii) 40, 60, 80 

17. முக்கோணத்தின் ஒரு கோணம் 65° மற்ற இரு கோணங்களின் வித்தியாசம் 45° எனில், அவ்விரு கோணங்கள் 

i) 85°, 40° 

ii) 70°, 25° 

iii) 80°, 35°  

iv) 80°, 135°

விடை : iii) 80° , 35° 

18. கொடுக்கப்பட்டுள்ள படத்தில் AB, CD ஆகியவை இணையானவை எனில் b இன் மதிப்பு

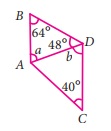
i) 112° 

ii) 68° 

iii) 102°

iv) 62°

விடை : ii) 68°

19. கொடுக்கப்பட்டுள்ள படத்தில் பின்வரும் கூற்றுகளில் எது சரியானது? 

i) x + y + z = 180°

ii) x + y + z = a + b + c 

iii) x + y + z = 2 (a + b + c) 

iv) x + y + z = 3 (a + b + c)

விடை : iii) x + y + z = 2 (a + b + c) 

20. ஒரு முக்கோணத்தில் ஒரு வெளிக்கோணம் 70° மற்றும் அதன் உள்ளெதிர்க் கோணங்கள் சமம் எனில், அக்கோணத்தின் அளவானது. 

i) 110°

ii) 120° 

iii) 35°

iv) 60° 

விடை : iii) 35°

21. ΔABC இல் AB = AC எனில் x இன் மதிப்பு ________

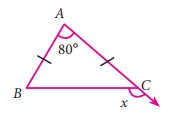
i) 80°

ii) 100° 

iii) 130° 

iv) 120° 

விடை : iii) 130° 

22. ஒரு முக்கோணத்தில் ஒரு வெளிக்கோணம் 115° மற்றும் ஒரு உள்ளெதிர்க் கோணம் 35° எனில் முக்கோணத்தின் மற்ற இரண்டு கோணங்கள் 

i) 45°, 60° 

ii) 65°, 80° 

iii) 65°, 70°

iv) 115°, 60° 

விடை : ii) 65°, 80°

விடைகள் :

பயிற்சி  4.1

1. ஆம் 

2. இல்லை, கொடுக்கப்பட்ட கோணங்கள் ஒரு முக்கோணத்தை அமைக்காது. 

3. (i) 45º (ii) 62º (iii) 30º (iv) 17º (v) 18º (vi) 20º (vii) 24º (viii) 27º

4. ∠A = 60º; ∠B = 40º

5. 360º

6. 45º,60º,75º

7. 55º,60º,65º

8. 30º,60º,90º

9. ∠X = 60º; ∠Z = 48º

10. ∠A = 29º; ∠C = 61º

11. ∠M = 38º; ∠O = 52º

12.(i) 110º (ii) 11º

13. 21º

14. 110º

15. 120º

கொள்குறி வகை வினாக்கள் 

16.(ii) 40º, 60º, 80º

17. (iii) 80º, 35º

18. (ii) 68º

19. (iii) x + y + z = 2(a + b + c)

20. (iii) 35º

21. (iii) 130º

22. (ii) 65º, 80º