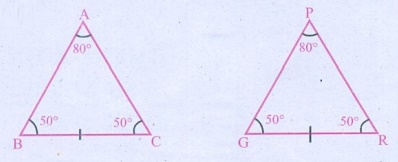
வடிவியல் | இரண்டாம் பருவம் அலகு 4 | 7ஆம் வகுப்பு கணக்கு - சர்வசம முக்கோணங்கள் (Congruency of Triangles) | 7th Maths : Term 2 Unit 4 : Geometry
7ஆம் வகுப்பு கணக்கு : இரண்டாம் பருவம் அலகு 4 : வடிவியல்
சர்வசம முக்கோணங்கள் (Congruency of Triangles)
சர்வசம முக்கோணங்கள் (Congruency of Triangles)
வடிவியலில் முக்கியக் கருத்தான 'சர்வசமம்’ என்பதை நாம் கற்போம். சர்வசம முக்கோணங்களைப் புரிந்துகொள்வதற்கு முதலில் வடிவங்களின் சர்வசமம் பற்றி அறிந்துகொள்ளலாம்.
1. சர்வசம வடிவங்கள் (Congruency of Shapes)
பின்வரும் பொருள்களின் படங்களை நன்கு கவனிக்க.

வடிவங்களின் சர்வசமத்தைப் புரிந்துகொள்வதற்கு நாம் விளையாடும் சீட்டுக்கட்டினை எடுத்துக்கொள்வோம். அவற்றில் ஏதேனும் இரு சீட்டுகளை எடுத்து ஒன்றின் மீது மற்றொன்றை வைக்கவும். அவை ஒன்றோடொன்று அளவிலும் வடிவத்திலும் மிகச் சரியாகப் பொருந்துமாறு வைக்க முடியும். ஆகவே கட்டில் உள்ள அனைத்துச் சீட்டுகளும் ஒன்றுக்கொன்று சர்வ சமமானவை ஆகும்.
மேற்குறிப்பிட்ட பண்புடன் கூடிய ஏதேனும் இரு பொருள்கள் சர்வசமமானவை என்றழைக்கப்படும்.
இரு பொருள்கள் அல்லது உருவங்களின் சர்வசமத் தன்மையை எவ்வாறு அறிவது?
உருவங்களின் சர்வசமத் தன்மையைச் சரிபார்த்தலுக்கு நாம் ஒன்றின் மீது ஒன்று பொருத்தும் முறையைப் பயன்படுத்துகிறோம். இம்முறையில், ஓர் உருவத்தைப் படி எடுத்து, படி எடுத்த உருவத்தை மற்றோர் உருவத்தின் மீது பொருத்துதல் வேண்டும். இரண்டு உருவங்களும் ஒன்றின் மீது ஒன்று பொருந்துமாயின்அவை சர்வசம உருவங்களாகும். இம்முறையில் படியெடுத்த உருவத்தை மடிக்கவோ நீட்டவோ செய்தல் கூடாது. ஆனால் நகர்த்தலாம் அல்லது சுழற்றலாம்.
2. சர்வசமக் கோடுகள் (Congruence of Line Segments)
கீழ்க்காணும் நேர்க்கோட்டுத் துண்டுகளின் அளவுகளைக் கூர்ந்து கவனிக்க.
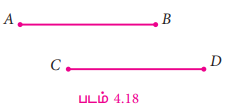
கோட்டுத்துண்டுகள் s ![]() யும்,
யும், ![]() -யும் ஒரே நீளம் கொண்டவை. மேற்பொருத்தும் முறை மூலம்
-யும் ஒரே நீளம் கொண்டவை. மேற்பொருத்தும் முறை மூலம் ![]() -யும்,
-யும், ![]() -யும் ஒன்றின் மீது ஒன்று சரியாகப் பொருந்துவதைக் காணலாம். எனவே, அக்கோட்டுத் துண்டுகள் சர்வசமக் கோட்டுத்துண்டுகள் ஆகும். இதை
-யும் ஒன்றின் மீது ஒன்று சரியாகப் பொருந்துவதைக் காணலாம். எனவே, அக்கோட்டுத் துண்டுகள் சர்வசமக் கோட்டுத்துண்டுகள் ஆகும். இதை ![]() ≈
≈ ![]() என எழுதலாம்.
என எழுதலாம்.
கோட்டுத்துண்டுகளின் சர்வசமத் தன்மைக்கு, நீளத்தை மட்டும் எடுத்துக்கொள்வதால் ![]() ≈
≈ ![]() என்பதை
என்பதை ![]() =
= ![]() எனவும் எழுதலாம். எனவே கோட்டுத்துண்டுகளின் நீளங்கள் சமமெனில் அவைகள் சர்வசமக் கோட்டுத்துண்டுகளாகும்.
எனவும் எழுதலாம். எனவே கோட்டுத்துண்டுகளின் நீளங்கள் சமமெனில் அவைகள் சர்வசமக் கோட்டுத்துண்டுகளாகும்.
இவற்றை முயல்க
பின்வரும் கோட்டுத்துண்டுகளை அளந்து சர்வசமக் கோட்டுத்துண்டுகளின் இணைகளாக வகைப்படுத்துக.
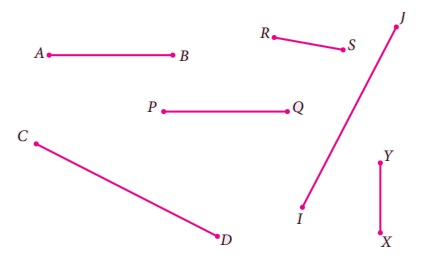
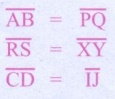
3. சர்வசமக் கோணங்கள் (Congruence of Angles)
பின்வரும் கோணங்களைக் கவனிக்க.
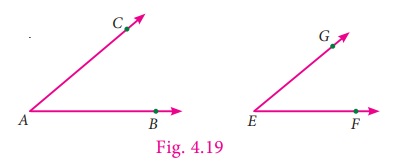
∠BAC , ∠FEG ஆகிய கோணங்களின் சர்வசமத் தன்மையை சோதிப்பதற்கு, ∠BAC ஐ படி எடுத்து, AB ஆனது கோணம் ∠FEG இல் FE மீது பொருந்துமாறு செய்வோம். இப்போது AC ஆனது FG இன் மீது அமையும். கோணத்தின் கதிர்களின் நீளங்கள் வேறுபட்டாலும், ∠BAC ஆனது ∠FEG இன் மீது முழுவதுமாக பொருந்தும். எனவே, அவை சர்வசமக் கோணங்கள் ஆகும். இதை ∠BAC ≅ ∠FEG எனக் குறிப்போம்.
சர்வசமக் கோணங்கள் அவற்றின் கோண அளவை மட்டுமே சார்ந்தவை. கதிர்களின் நீளங்களைச் சார்ந்தவை அல்ல. எனவே, இரு கோணங்களின் கோண அளவுகள் சமம் எனில், அவை சர்வசமக் கோணங்கள் என அழைக்கப்படும்.
இரு கோணங்கள் ∠BAC , ∠FEG ஆகியன சர்வசமம் எனில், அதனை ∠BAC ≅ ∠FEG என்று குறிக்கலாம்.
கோட்டுத்துண்டுகளைப் போன்றே கோணங்களின் சர்வசமத் தன்மையும் கோணங்களின் அளவைப் பொறுத்தே அமைவதால் இரு கோணங்கள் சர்வசமம் எனில், அவ்விரு கோண அளவுகளும் சமமானவையாக இருக்கும்.
ஆகவே, ∠BAC ≅ ∠FEG என்பதை ∠BAC ≅ ∠FEG என்றும் எழுதலாம்.
இவற்றை முயல்க
சர்வசமக்கோண சோடிகளை மேற்பொருத்தும் முறை அல்லது கோணங்களை அளப்பதன் மூலம் கண்டறிக.
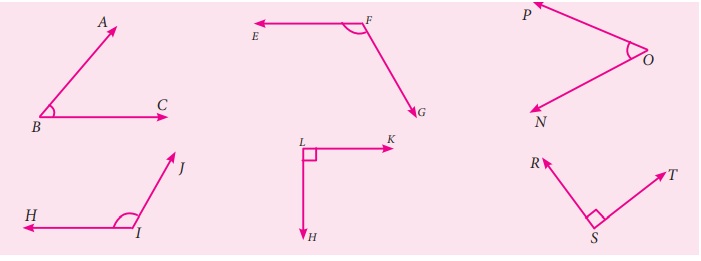
விடைகள் :
∠ABC ≈ ∠PON
∠EFG ≈ ∠HIJ
∠HLK ≈ ∠RST
4. சர்வசமத் தள உருவங்கள் (Congruence of Plane Figures)
கீழ்க்காணும் தள உருவங்களைக் கவனிக்க.
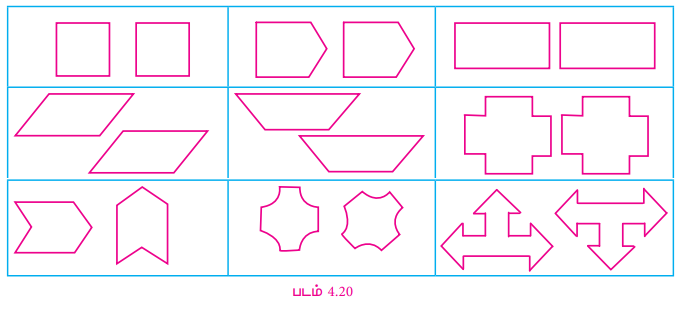
அவை வடிவத்திலும் அளவிலும் ஒரே அளவு கொண்டவை. பக்கங்களும் (கோட்டுத்துண்டுகள்), கோணங்களும் சம அளவு கொண்டவை.
கீழ்க்காணும் வட்டங்களைக் கவனிக்க படம் 4.21.
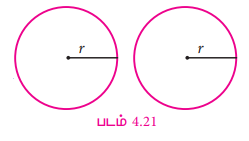
அவற்றின் ஆரங்கள் சமம். அவை ஒன்றின் மீது ஒன்று முழுவதுமாகப் பொருந்துகிறது. இவ்வாறான உருவங்கள் சர்வசமத் தள உருவங்கள் எனப்படும்.
குறிப்பு
சர்வசமத் தன்மையுடைய வடிவங்களில் ஒன்றின் மீது ஒன்று முழுவதுமாகப் பொருந்தும் பகுதிகள் ஒத்த பகுதிகள் என அழைக்கப்படும். மேற்பொருந்தும் பக்கங்கள் ஒத்த பக்கங்கள் என்றும், மேற்பொருந்தும் கோணங்கள் ஒத்த கோணங்கள் என்றும் அழைக்கப்படும்.
எனவே, இரண்டு தள உருவங்களில் ஒத்த பக்கங்கள் மற்றும் ஒத்த கோணங்கள் சமமெனில், அவை சர்வசம உருவங்கள் எனப்படும். இரண்டு தள உருவங்கள் F1, F2 ஆகியவை சர்வசமமெனில் அவற்றை F1 ≅ F2 என எழுதலாம்.
5. சர்வசம முக்கோணங்கள் (Congruence of Triangles)
மூன்று கோட்டுத்துண்டுகளால் அமைக்கப்படும் மூடிய வடிவமே முக்கோணம் என நாம் அறிவோம். ஒரு முக்கோணத்தில் மூன்று பக்கங்களும், மூன்று கோணங்களும் உள்ளன. இரு முக்கோணங்களில், ஒத்த பக்கங்களும், ஒத்த கோணங்களும் சமம் எனில், அவை சர்வசம முக்கோணங்கள் எனப்படும்.
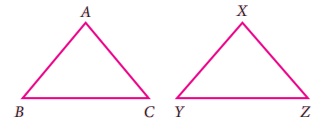
பின்வரும் இரு முக்கோணங்களான ∆ABC மற்றும் ∆XYZ ஐ உற்று நோக்குக.
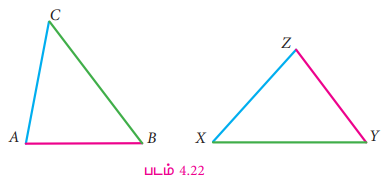
படி எடுத்து மேற்பொருத்தும் முறையில், ∆XYZ ஆனது ∆ABC ன் மீது முழுவதுமாகப் பொருந்துவதைக் காண இயலும்.
∆ABC இன் அனைத்துப் பக்கங்களும், கோணங்களும், ∆XYZ இன் ஒத்த பக்கங்களுக்கும், ஒத்த கோணங்களுக்கும் சமமாக உள்ளன. எனவே, அவை சர்வசம முக்கோணங்கள் எனக் கூற முடியும். இதனை ∆ABC ≅ ∆XYZ என எழுதலாம்.
முனைகள் A, B மற்றும் C ஆகியவை முறையே முனைகள் Z, Y மற்றும் X இன் மீது பொருந்துவதைக் காணலாம். அவை ஒத்த முனைகள் என அழைக்கப்படும்.
பக்கங்கள் AB, BC மற்றும் CA ஆகியவை முறையே பக்கங்கள் YZ, XY மற்றும் ZX ஆகியவை மீது முழுவதுமாகப் பொருந்துகின்றன. எனவே அவை ஒத்த பக்கங்கள் எனப்படும்.
மேலும், ∠A = ∠Z , ∠B = ∠Y மற்றும் ∠C = ∠X இவை ஒத்த கோணங்கள் எனப்படும்.
மேலே உள்ள முக்கோணங்களின் முனைகளை A ↔ Z, B ↔ Y, C ↔ X என தொடர்பு படுத்தலாம். நாம் இதனை ABC ↔ XYZ என எழுதலாம்.
முனை A இன் மீது முனை Y அல்லது முனை X ஐ பொருத்தும்போது, முக்கோணங்கள் ஒன்றின் மீது ஒன்று முழுவதும் பொருந்தாத தன்மையை நாம் காணலாம். இதிலிருந்து முக்கோணங்கள் சர்வசமமற்றவை என்று கூற முடியாது.
இதன்மூலம், முக்கோணங்களின் சர்வசமத் தன்மையைப் உறுதி செய்வதற்கு ஒத்த முனைகள், ஒத்த பக்கங்கள், ஒத்த கோணங்களை சரிபார்க்க வேண்டும்.
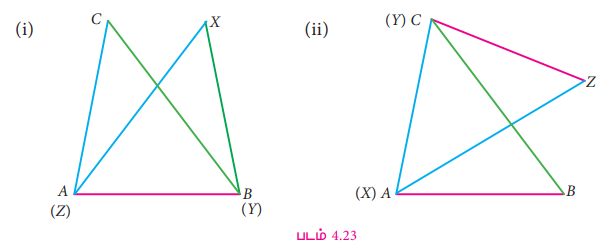
எனவே, மேற்கண்ட முக்கோணங்கள் (∆ABC ≅ ∆XYZ) என்பது சர்வசமமானவை.
ஆகவே, ஒரு முக்கோணத்தின் அனைத்துப் பக்கங்களும், அனைத்துக் கோணங்களும் மற்றொரு முக்கோணத்தின் ஒத்த பக்கங்கள் மற்றும் கோணங்களுக்குச் சமம் எனில், அவ்விரண்டு முக்கோணங்களும் சர்வசம முக்கோணங்கள் என்று கூறலாம்.
6. சர்வசம முக்கோணங்களுக்கான விதிகள் (Conditions for Triangles to be Congruent)
முக்கோணங்களின் சர்வசமத் தன்மையை உறுதி செய்வதற்கு மேற்பொருத்தும் முறையைக் கற்றுக்கொண்டோம். மிகவும் பயனுள்ள பொருத்தமான அளவீடுகளைப் பயன்படுத்தி முக்கோணங்களின் சர்வசமத் தன்மையை சரிபார்க்கலாம். அவற்றை முக்கோணங்களின் சர்வசமத் தன்மையைச் சரிபார்க்க உதவும் கொள்கைகளாக நாம் பின்வருமாறு அறிந்து கொள்ளலாம்.
பின்வரும் முக்கோணத்தைக் கவனிக்க (படம் 4.24).
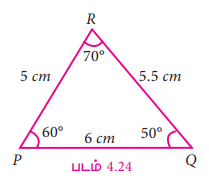
மேற்கண்ட முக்கோணத்திற்குச் சர்வசமமாக மற்றொரு முக்கோணத்தை வரைவதற்கு அனைத்து அளவுகளும் கொடுக்கப்படுதல் அவசியமா? முக்கோணத்தை வரைய மூன்று அளவுகள் மட்டுமே போதுமானதாகும். அம்மூன்று அளவுகள் பின்வருவனவற்றில் ஏதேனும் ஒன்றாக இருக்கலாம் (படம் 4.24).
1. மூன்று பக்கங்களின் அளவுகள் (அல்லது)
2. இரண்டு பக்க அளவுகள் மற்றும் கொடுக்கப்பட்ட பக்கங்களுக்கு இடைப்பட்ட கோணம் (அல்லது)
3. இரண்டு கோணங்கள் மற்றும் கொடுக்கப்பட்ட கோணங்களைத் தாங்கும் பக்கம்.
இம்மூன்று கொள்கைகளையும் ஒவ்வொன்றாகப் பார்க்கலாம்.
1. மூன்று பக்கங்களின் அளவுகள் கொடுக்கப்பட்டுள்ளது. பக்கம்-பக்கம்-பக்கம் கொள்கை (ப-ப-ப)
XY = 6 செ.மீ, YZ = 5.5 செ.மீ, மற்றும் ZX = 5 செ.மீ, என உள்ளவாறு ∆XYZ ஐ வரைக.
படி 1: ஒரு நேர்கோடு வரைக. XY = 6 செ.மீ உள்ளவாறு கோட்டின் மீது X மற்றும் Y ஐக் குறிக்க.

படி 2: ஆரம் 5 செ.மீ உள்ளவாறு X ஐ மையமாகக் கொண்டு ஒரு வட்ட வில்லை XY இக்கு மேற்புறம் வரைக.
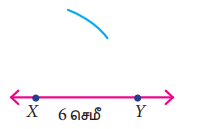
படி 3: Y ஐ மையமாகக் கொண்டு 5.5 செ.மீ ஆரம் கொண்ட வட்ட வில்லை முன்னர் வரைந்த வட்ட வில்லை வெட்டுமாறு வரைக. வெட்டும் புள்ளியை Z எனக் குறிக்க.
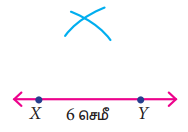
படி 4: XZ மற்றும் YZ ஐ இணைக்க.
XYZ தேவையான முக்கோணம் ஆகும்.
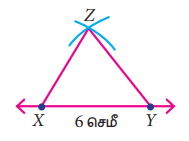
மேற்பொருத்தும் முறையில் ∆PQR (படம் 4.24) இன் மீது பக்கங்கள் XY, PQ; XZ, PR; YZ, QR என்றவாறு ∆XYZ ஐப் பொருத்தினால் இரு முக்கோணங்களும் மிகச் சரியாகப் பொருந்துவதைக் காணலாம். எனவே, முக்கோணங்கள் ∆PQR உம் ∆XYZ உம் சர்வசம முக்கோணங்கள் ஆகும். இதனை ∆PQR = ∆XYZ எனக் குறிக்கிறோம்.
இங்கு பக்கங்கள் மட்டும் முதன்மையாகக் கொடுக்கப்பட்டிருப்பதால் இக்கொள்கையை ஒரு முக்கோணத்தின் மூன்று பக்கங்கள் மற்றொரு முக்கோணத்தின் ஒத்த பக்கங்களுக்குச் சமம் எனில், அவ்விரு முக்கோணங்களும் சர்வசம முக்கோணங்கள் ஆகும். இது பக்கம்-பக்கம்-பக்கம் (ப-ப-ப) கொள்கை என அறியப்படும்.
குறிப்பு
இரண்டு முக்கோணங்கள் சர்வசமம் எனில் அவற்றின் ஒத்த பாகங்கள் சர்வசமம் ஆகும். இதை 'சர்வசம முக்கோணங்களின் ஒத்த பக்கங்கள் சர்வசமம்' என்று கூறுவோம்.
2. இரண்டு பக்க அளவுகள் மற்றும் கொடுக்கப்பட்டுள்ள பக்கங்களுக்கு இடைப்பட்ட கோணம் கொடுக்கப்பட்டிருத்தல். பக்கம்-கோணம்-பக்கம் கொள்கை (ப-கோ-ப).
AB = 6 செ.மீ, AC = 5 செ.மீ மற்றும் ∠A = 60° உள்ளவாறு ∆ABC வரைக.
படி 1: ஒரு நேர்கோடு வரைக. AB = 6 செ.மீ உள்ளவாறு A மற்றும் B என்ற புள்ளிகளை அதன் மீது குறிக்க.

படி 2: A இல் AB உடன் 60° கோணத்தை அமைக்குமாறு AX என்ற கதிரை வரைக.

படி 3: A ஐ மையமாகக் கொண்டு 5 செ.மீ ஆரம் கொண்ட வட்ட வில்லைக் கதிர் AX ஐ வெட்டுமாறு வரைக. வெட்டும் புள்ளியை C எனக் குறிக்க.
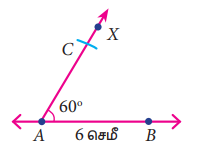
படி 4: BC ஐ இணைக்க.
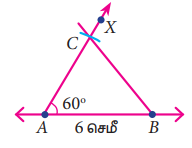
ABC என்பது தேவையான முக்கோணம் ஆகும்.
மேற்பொருத்தும் முறையில், ∆ABC ஐ ∆PQR (படம் 4.24) இன் மீது, AB, PQ; AC, PR மற்றும் ∠A, ∠P என்றவாறு பொருத்தினால் இரு முக்கோணங்களும் ∆ABC, ∆PQR மிகச் சரியாகப் பொருந்துவதைக் காணலாம்.
“ஒரு முக்கோணத்தின் இரு பக்கங்களும், அப்பக்கங்களுக்கு இடைப்பட்ட கோணமும் மற்றொரு முக்கோணத்தின் ஒத்த இரு பக்கங்களுக்கும், அவற்றிற்கிடைப்பட்ட கோணத்திற்கும் சமமாக இருந்தால் அம்முக்கோணங்கள் சர்வசம முக்கோணங்கள்” எனக் கூறுவோம். இது பக்கம்-கோணம்-பக்கம் கொள்கை என அழைக்கப்படும்
3. இரண்டு கோணங்கள் மற்றும் கொடுக்கப்பட்ட கோணங்களைத் தாங்கும் பக்கம் கொடுக்கப்பட்டிருத்தல். கோணம்-பக்கம்-கோணம் கொள்கை (கோ-ப-கோ).
LM = 5.5 செ.மீ, ∠M = 70°d ∠L = 50° உள்ளவாறு ∆LMN.
படி 1: ஒரு நேர் கோடு வரைக. LM = 5.5 செ.மீ உள்ளவாறு L மற்றும் M என்ற புள்ளிகளை அதன்மீது குறிக்க.

படி 2: L இல் LM உடன், 50° கோணத்தை ஏற்படுத்துமாறு கதிர் LX வரைக.
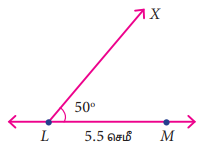
படி 3: M இல் LM உடன், 70° கோணத்தை ஏற்படுத்துமாறு கதிர் MY வரைக. இரு கதிர்களும், வெட்டிக் கொள்ளும் புள்ளியை N எனக் குறிக்க.
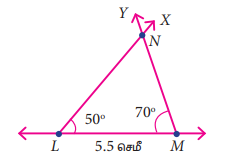
LMN என்பது தேவையான முக்கோணம் ஆகும்.
மேற்பொருத்தும் முறையில் ∆PQR (படம் 4.24) இன் மீது ∠L, ∠Q; ∠M , ∠R மற்றும் LM, QR என்றவாறு ∆LMN ஐப் பொருத்துக. இரு முக்கோணங்களும் மிகச் சரியாகப் பொருந்துவதைக் காணலாம்.
“ஒரு முக்கோணத்தின் இரு கோணங்களும், கோணத்தைத் தாங்கும் பக்கமும் மற்றொரு முக்கோணத்தின் ஒத்த பகுதிகளுக்குச் சமமாக இருந்தால் அம்முக்கோணங்கள் சர்வசமம்" என்று கூறுவோம். இது கோணம்-பக்கம்-கோணம் கொள்கை என அழைக்கப்படும்.
குறிப்பு
முக்கோணங்களின் சர்வசமத் தன்மையைச் சரிபார்த்தலுக்கு மேலும் ஒரு கொள்கை உள்ளது. இக்கொள்கையானது கோணம்-கோணம்-பக்கம் என அழைக்கப்படும். இது கோ-ப-கோ கொள்கையைச் சற்றே மாற்றியமைப்பதன் மூலம் கிடைக்கிறது. இதில் இரு கோணங்களும், கோணங்களுக்கு இடையில் அமையாத பக்கமும் பயன்படுத்தப்படும்.
இக்கொள்கையை, "ஒரு முக்கோணத்தில் இரு கோணங்களும், கோணங்களைத் தாங்காத மற்ற ஒரு பக்கமும் மற்றொரு முக்கோணத்தின் ஒத்த பாகங்களுக்குச் சமமாக இருந்தால், அவ்விரு முக்கோணங்கள் சர்வசமமாக இருக்கும்" எனக் கூறுவோம்.
கர்ணம் (Hypotenuse)
நாம், முந்தைய வகுப்பில் செங்கோண முக்கோணத்தைக் கற்றறிந்துள்ளோம். ஒரு செங்கோண முக்கோணத்தில், ஒரு கோணம் செங்கோணமாகவும் மற்ற இரு கோணங்கள் குறுங்கோணங்களாகவும் அமைந்திருக்கும். பின்வரும் செங்கோண முக்கோணங்களைக் கவனிக்க.
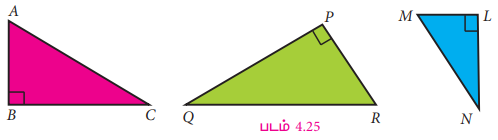
அனைத்து முக்கோணங்களிலும், செங்கோணத்திற்கு எதிரேயுள்ள பக்கமே அதிக நீளமுடையதாக உள்ளது. இந்தப் பக்கம் கர்ணம் என அழைக்கப்படும்.
மேற்கண்ட முக்கோணங்களில் AC, QR மற்றும் MN ஆகிய பக்கங்கள், கர்ணமாக அமைந்துள்ளன. கர்ணம் என்பது செங்கோண முக்கோணத்துடன் மட்டும் தொடர்புடையதாகும்.
4. செங்கோணம்-கர்ணம்-பக்கம் கொள்கை (செ-க-ப) (Right Angle - Hypotenuse - Side congruence crieterion (RHS))
இக்கொள்கையானது செங்கோண முக்கோணங்களில் மட்டுமே பயன்படுத்தப்படும் என்பது தெளிவு.
பின்வரும் இரு செங்கோண முக்கோணங்களை உற்றுநோக்குக.
இவ்விரு முக்கோணங்களிலும் செங்கோணம் பொதுவான கோணம். மேலும் செங்கோணத்தை உருவாக்கும் இரு பக்கங்களின் நீளங்கள் கொடுக்கப்பட்டால் ப-கோ-ப கொள்கையைப் பயன்படுத்துவதன் மூலம் முக்கோணங்களின் சர்வசமத் தன்மையைச் சரிபார்க்க இயலும்.
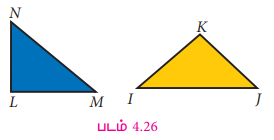
அவ்வாறில்லாமல், செங்கோணத்தை அமைக்கும் ஒரு பக்கமும், கர்ணமும் கொடுக்கப்படும்போது, ஒரு புதிய கொள்கை நமக்குக் கிடைக்கிறது. "ஒரு செங்கோண முக்கோணத்தின் கர்ணமும், ஒரு பக்கமும் மற்றொரு செங்கோண முக்கோணத்தின் கர்ணத்திற்கும் ஒரு பக்கத்திற்கும் சமமாக இருந்தால் அவ்விரு செங்கோண முக்கோணங்களும் சர்வசமம் ஆகும்."
இது செங்கோணம்-கர்ணம்-பக்கம் கொள்கை (செ-க-ப) எனப்படும்.
குறிப்பு
முக்கோணங்களின் சர்வசமத் தன்மைக்கான முக்கோணங்களின் கொள்கைகளைக் கற்றோம். சர்வசமத் தன்மையைச் சரிபார்த்தலுக்குப் பின்வரும் கொள்கைகள் போதுமானதாக அமையாது கோணம்-கோணம்-கோணம் (கோ-கோ-கோ) கொள்கையானது முக்கோணங்கள் எப்போதும் சர்வசமம் என்பதை நிரூபிக்காது. இதன் மூலம் முக்கோணங்கள் ஒரே வடிவத்தில் அமையும் என்பதை மட்டுமே அறிய இயலும். ஒரே அளவுடையவை என்பதை அறிய இயலாது. பக்கம்-பக்கம்-கோணம் (அல்லது) கோணம்-பக்கம்-பக்கம் (ப-ப-கோ அல்லது கோ-ப-ப). இக்கொள்கையின் மூலமும் முக்கோணங்களின் சர்வசமத் தன்மையை அறிய இயலாது. இக்கொள்கையில் இரு பக்கங்களும் அப்பக்கங்களில் அமையாத கோணமும் பயன்படுத்தப்படுகின்றன.
இவற்றை முயல்க
(i) ∆ABC ≅ ∆XYZ எனில், ஒத்த பக்கங்கள் மற்றும் ஒத்த கோணங்களை எழுதுக.
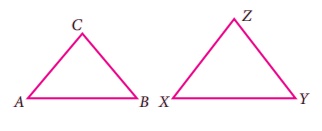
விடை : ∠A = ∠X, ∠B = ∠Y, ∠C = ∠X
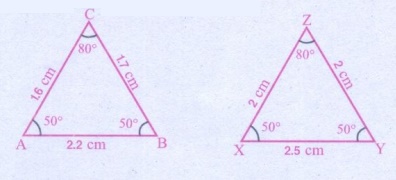
(ii) கொடுக்கப்பட்ட முக்கோணங்கள் சர்வசமம் எனில், ஒத்த பாகங்களைக் கண்டுபிடித்து சர்வசமக் கூற்றை எழுதுக.
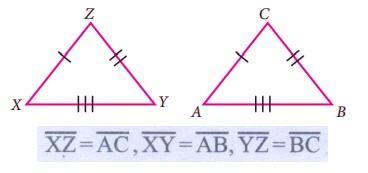
By SSS law, ∆XYZ ≅ ∆ ABC
(iii) கொடுக்கப்பட்டுள்ள முக்கோணங்களின் சர்வசமத்தை உறுதி செய்வதற்கு மேற்குறிப்பிட்டுள்ள கொள்கைகளின்படி தேவைப்படும் நிபந்தனைகளைக் குறிப்பிடுக. விடைகளுக்குத் தகுந்த காரணத்தைக் குறிப்பிடுக.
விடை :
∠A = ∠P, ∠B = ∠Q, ∠C = ∠R
By AAA law, ∆ABC ≅ ∆ PQR