இணைகரத்தின் பரப்பளவு மற்றும் சுற்றளவு

இணைகரம்

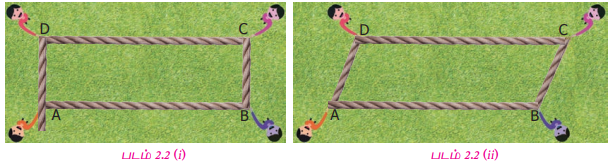
ஏதேனும் நான்கு மாணவர்களைக் கயிறு கொண்டு வரச் சொல்லிப் படம் 2.2 (i)இல் காட்டியுள்ளவாறு ABCD என்ற செவ்வகத்தை அமைக்கச்செய்தல் வேண்டும். பின்னர் C, D இல் நிற்கும் மாணவர்களை அவர்களுக்கு இடதுபுறமாக நான்கு சமமான அடிகள் நகர்ந்து படம் 2.2(ii) இல் காட்டியுள்ளவாறு ஒரு வடிவத்தை உருவாக்கச்செய்தல் வேண்டும்.

இப்போது உருவாக்கப்பட்ட புதிய வடிவமே இணைகரம் ஆகும். இங்கு AB மற்றும் CD என்ற ஒரு சோடி பக்கங்கள் ஒன்றுக்கொன்று இணையாகவும் உள்ளன. மேலும், BC மற்றும் AD யும் ஒன்றுக்கொன்று இணையாக உள்ளன. இணைப்பக்கங்களின் நீளங்கள் ஒன்றுக்கொன்று சமமாக உள்ளன. எனவே, எதிர்ப் பக்கங்கள் இணையாகவும் சமமாகவும் உள்ள நான்கு பக்கங்கள் கொண்ட ஓர் மூடிய வடிவமானது இணைகரம் என்ற முடிவுக்கு நாம் வரலாம்.

எங்கும் கணிதம் - அன்றாட வாழ்வில் அளவியல்

இணைகரத்தின் பரப்பளவு மற்றும் சுற்றளவு

படம் 2.3(i)இல் காட்டியுள்ளவாறு ஒரு வரைபடத்தாளில் ஓர் இணைகரத்தை வரைந்து அதை வெட்டி எடுத்துக்கொள்ள வேண்டும். ஒரு முனையிலிருந்து எதிர்ப்பக்கத்திற்கு ஒரு செங்குத்துக் கோடு வரைக. படம் 2.3(ii)இல் காட்டியுள்ளவாறு முக்கோணத்தை வெட்டி இணைகரத்தின் மறு பக்கத்திற்குக் கொண்டு செல்லவேண்டும், தற்போது என்ன வடிவத்தைக் காண்கிறோம்? அது ஒரு செவ்வகம். (படம் 2.3(iii)). எனவே, இணைகரத்தின் பரப்பளவானது செவ்வகத்தின் பரப்பளவிற்குச் சமமாக இருக்கிறது.

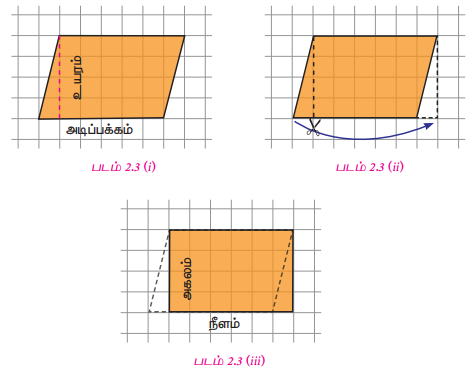
எனவே, செவ்வகத்தின் பரப்பளவு = நீளம் × அகலம்

= அடிப்பக்கம் × உயரம் ச.அலகுகள் 

= இணைகரத்தின் பரப்பு

மேலும், இணைகரத்தின் சுற்றளவு என்பது அதன் நான்கு பக்கங்களின் கூடுதல் ஆகும்.

சிந்திக்க

1. ஓர் இணைகரத்தின் பரப்பளவை இரண்டு முக்கோணத்தின் பரப்பளவுகளாக எழுதலாம் என்பதை விவரி. 

2. ஒரு செவ்வகம் இணைகரமாகும், ஆனால் ஓர் இணைகரமானது செவ்வகம் ஆகாது, ஏன்?

இவற்றை முயல்க 

1. பின்வரும் இணைகரங்களைச் சமப்பரப்பளவு கொண்ட செவ்வகங்களாக மாற்றிக் கட்டங்களைக் கூட்டும் முறையைப் பயன்படுத்திப் பரப்பளவு காண்க. (உயரத்தையும் அடிப்பக்கத்தையும் மாற்றாமல்).

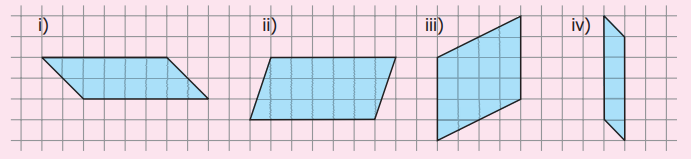
i)_____ ச.அலகுகள் ii) _____ ச.அலகுகள் iii)_____ ச.அலகுகள் iv)_____ ச.அலகுகள்

i) 12 ச.அலகுகள் ii)   18 ச.அலகுகள்   iii) 16 ச.அலகுகள்      iv) 5 ச.அலகுகள்

2. கொடுக்கப்பட்டுள்ள இணைகரங்களுக்கு உயரங்கள் வரைந்து அடிப்பக்கங்களைக் குறித்துப் பரப்பளவு காண்க. உங்கள் முடிவுகளை ஆராய்க.

(i)

பரப்பளவு : 4 × 2 = 8 ச.அ

சுற்றளவு  : 4+2+4+2=12 அலகுகள் 

(ii)

பரப்பளவு: 4 × 2 = 8 ச.அ

சுற்றளவு : 4+2.5+4+2.5=13 அலகுகள்

(iii)

பரப்பளவு: 4 × 2 = 8 ச.அ

சுற்றளவு : 4+3+4+3=14 அலகுகள்

(iv)

பரப்பளவு: 4 × 2 = 8 ச.அ

சுற்றளவு : 4+4+4+4 = 16 அலகுகள்

(v)

பரப்பளவு: 4 × 2 = 8 ச.அ

சுற்றளவு : 4+5+4+5 = 18 அலகுகள்

3. கொடுக்கப்பட்டுள்ள ஒவ்வொரு இணைகரத்திற்கும் அடிப்பக்கத்தையும், உயரத்தையும் அளந்து, சூத்திரத்தைப் பயன்படுத்திப் பரப்பளவைக் காண்க.

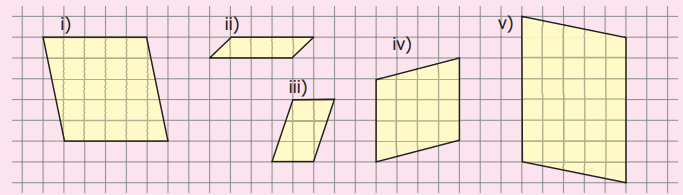
i) __ ச.அலகுகள் ii) __ ச.அலகுகள் iii) __ ச.அலகுகள் iv) __ ச.அலகுகள் v) __ ச.அலகுகள்

i) 25 ச.அலகுகள் 

ii) 4 ச.அலகுகள்

iii) 6 ச.அலகுகள்

iv) 16 ச.அலகுகள்

v) 35 ச.அலகுகள்

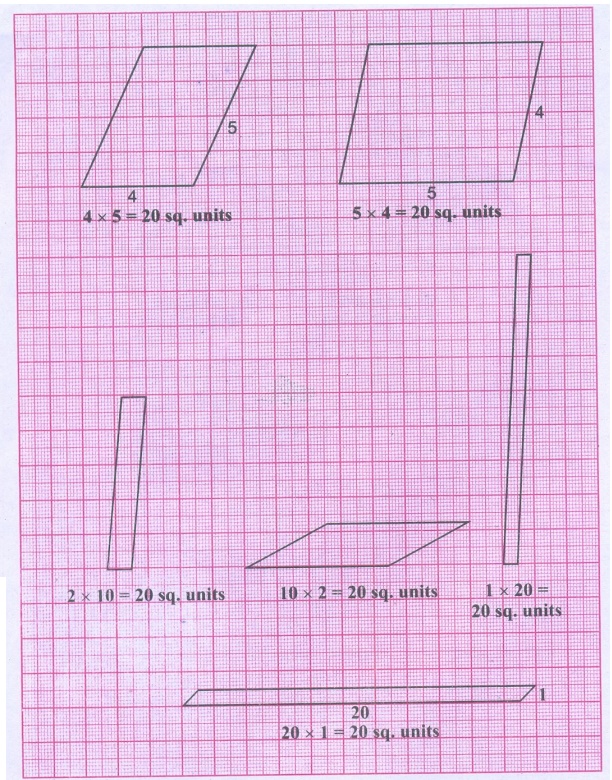
4. ஒரு தாளில் 20 சதுர அலகுகள் கொண்ட இணைகரங்கள் எவ்வளவு முடியுமோ அவ்வளவு வரைக.

எடுத்துக்காட்டு 2.1

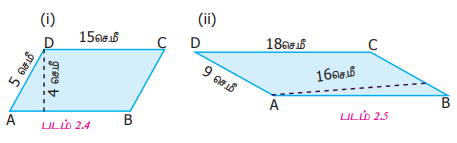
படத்தில் உள்ள இணைகரங்களின் பரப்பளவு மற்றும் சுற்றளவு காண்க. 

தீர்வு 

(i) படம் 2.4 லிருந்து, அடிப்பக்கம் (b) = 15 செ.மீ, உயரம் (h) = 4 செ.மீ

இணைகரத்தின் பரப்பளவு     = b × h. ச.அலகுகள்

= 15 × 4 = 60 ச.செ.மீ 

ஆகவே, இணைகரத்தின் பரப்பளவு 60 ச.செ.மீ ஆகும். 

இணைகரத்தின் சுற்றளவு       = நான்கு பக்கங்களின் நீளங்களின்  கூடுதல்

= (15+5+15+5) = 40 செ.மீ.

(ii) படம் 2.5 லிருந்து , 

அடிப்பக்கம் (b) = 9 செ.மீ, உயரம் (h) = 16 செ.மீ 

இணைகரத்தின் பரப்பளவு = b × h ச.அலகுகள்

= 9 × 16 = 144 ச.செ.மீ 

ஆகவே, இணைகரத்தின் பரப்பளவு 144 ச.செ.மீ ஆகும். 

இணைகரத்தின் சுற்றளவு  = நான்கு பக்கங்களின் நீளங்களின் கூடுதல்

= (18+9+18+9) = 54 செ.மீ.

எடுத்துக்காட்டு 2.2

அடிப்பக்கம் 12 மீ மற்றும் உயரம் 8 மீ அளவுகள் கொண்ட இணைகரத்தின் பரப்பளவு காண்க. 

தீர்வு 

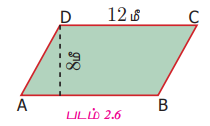
கொடுக்கப்பட்ட அளவுகள்: அடிப்பக்கம் (b) = 12 மீ, உயரம் (h) = 8 மீ 

இணைகரத்தின் பரப்பளவு = b × h ச.அலகுகள்

= 12 × 8 = 96 ச.மீ

ஆகவே, இணைகரத்தின் பரப்பளவு 96 ச.மீ ஆகும்.

எடுத்துக்காட்டு 2.3

பரப்பளவு 368 ச.செ.மீ மற்றும் அடிப்பக்கம் 23 செ.மீ அளவுகள் கொண்ட இணைகரத்தின் உயரம் காண்க.

தீர்வு 

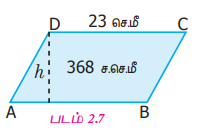
கொடுக்கப்பட்ட அளவுகள்: இணைகரத்தின் பரப்பளவு = 368 ச.செ.மீ , அடிப்பக்கம் (b) = 23 செ.மீ 

இணைகரத்தின் பரப்பளவு = 368 ச.செ.மீ

b × h = 368

23 × h = 368

 h = 368/23 = 16 செ.மீ

எனவே, இணைகரத்தின் உயரம் 16 செ.மீ ஆகும்.

எடுத்துக்காட்டு 2.4

ஓர் இணைகரத்தின் அடுத்தடுத்த பக்கங்கள் முறையே 12 செ.மீ மற்றும் 9 செ.மீ. சிறிய பக்கங்களுக்கு இடையே உள்ள தொலைவு 8 செ.மீ எனில் பெரிய பக்கங்களுக்கு இடையே உள்ள தொலைவைக் காண்க.

தீர்வு 

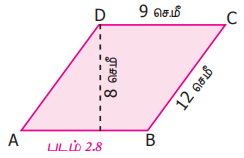
இணைகரத்தின் அடுத்துள்ள பக்கங்கள் 12 செ.மீ மற்றும் 9 செ.மீ எனக் கொடுக்கப்பட்டுள்ளது.

நாம் சிறிய பக்கத்தை அடிப்பக்கமாகக் கொண்டால், அதாவது b = 9 செ.மீ எனில், சிறிய பக்கங்களுக்கு இடையே உள்ள தொலைவு அதாவது h = 8 செ.மீ. 

எனவே இணைகரத்தின் பரப்பு = b × h ச. அலகுகள்

= 9 × 8 = 72 ச.செ.மீ. 

நாம் பெரிய பக்கத்தை அடிப்பக்கமாகக் கொண்டால், அதாவது b = 12 செ.மீ. 

எனில், பெரிய பக்கங்களுக்கு இடையே உள்ள தொலைவை 'h' என்க.

ஆகவே, இணைகரத்தின் பரப்பளவு = 72 ச.செ.மீ 

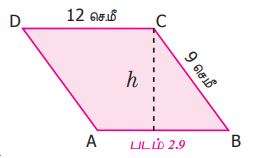
 b × h = 72

12 × h = 72

 h = 72/12 = 6 செ.மீ

எனவே, பெரிய பக்கங்களுக்கு இடையே உள்ள தொலைவு 6 செ.மீ ஆகும்.

எடுத்துக்காட்டு 2.5

ஓர் இணைகரத்தின் அடிப்பக்கமானது அதன் உயரத்தைப் போல மூன்று மடங்காகவும் அதன் பரப்பளவு 192 ச.செ.மீ ஆகவும் இருப்பின், அடிப்பக்கத்தையும் உயரத்தையும் காண்க. 

தீர்வு 

இணைகரத்தின் உயரத்தை 'h' செ.மீ எனக் கொள்க.

  எனவே, அடிப்பக்கம் = 3h செ.மீ

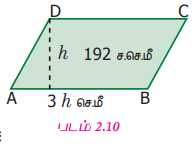
இணைகரத்தின் பரப்பளவு  = 192 ச.செ.மீ (கொடுக்கப்பட்டுள்ளது) 

b × h = 192 

3h × h = 192

3h2 = 192

 h2 = 64 

h × h = 8 × 8

h = 8 செ.மீ 

அடிப்பக்கம் = 3h = 3 × 8 = 24 செ.மீ 

எனவே, இணைகரத்தின் அடிப்பக்கம் 24 செ.மீ மற்றும் உயரம் 8 செ.மீ ஆகும்.

இணைகரத்தைப் பயன்படுத்திப் பெரும்பாலான பாலங்களின் உள்கட்டமைப்பு உருவாக்கப்பட்டுள்ளது. (எடுத்துக்காட்டு: இராமேஸ்வரத்தில் உள்ள பாம்பன் பாலம்).

பொறியாளர்கள் இணைகரங்களின் பண்புகளைப் பயன்படுத்திப் பாலங்களை உருவாக்கவும் பழுது பார்க்கவும் செய்கிறார்கள்.