சாய்சதுரத்தின் பரப்பளவு

சாய்சதுரம்

சம அளவுகள் கொண்ட நான்கு குச்சிகளையும், நான்கு வால்டியூப்களையும் எடுத்துக் கொள்க. படம் 2.11(i)இல் உள்ளவாறு நான்கு குச்சிகளையும் வால்டியூப்பையும் இணைத்து ஒரு சதுரம் உருவாக்குக, பிறகு படத்தில் காட்டியுள்ளவாறு எதிரெதிர் உச்சிகளை நெருக்கமாகக் கொண்டு வருக. (எதிர்ப் பக்கங்களின் இணை மாறாதவாறு). இப்போது கிடைக்கப்பெற்ற புதிய வடிவத்தையே சாய்சதுரம் என்கிறோம்.

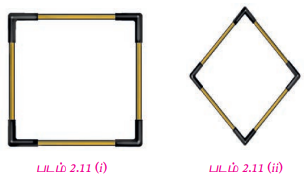
எனவே, ஓர் இணைகரத்தில் அனைத்துப் பக்கங்களும் சமமாக இருப்பின் அது ஒரு சாய்சதுரம் ஆகும்.

குறிப்பு 

ஒரு சாய்சதுரத்தில் 

(i) அனைத்துப் பக்கங்களும் சமம். 

(ii) எதிர்ப்பக்கங்கள் இணை . 

(iii) ஒரு சாய் சதுரத்தை அதன் மூலை விட்டம் சமப் பரப்பளவு கொண்ட நான்கு முக்கோணங்களாகப் பிரிக்கும். 

(iv) மூலை விட்டங்கள் ஒன்றுக்கொன்று செங்குத்தாக வெட்டிக்கொள்ளும்.

1. சாய்சதுரத்தின் பரப்பளவு (அடிப்பக்கமும், உயரமும் கொடுக்கப்பட்டிருப்பின்)

படம் 2.12(i)இல் காட்டியுள்ளவாறு ஒரு வரைபடத்தாளில் ஒரு சாய்சதுரத்தை வரைந்து அதை வெட்டி எடுத்துக்கொள்ள வேண்டும். ஒரு  முனையிலிருந்து எதிர்ப்பக்கத்திற்கு ஒரு செங்குத்துக்கோடு வரைக. படம் 2.12(ii) இல் காட்டியுள்ளவாறு முக்கோணத்தை வெட்டிச் சாய்சதுரத்தின் மறு பக்கத்திற்குக் கொண்டு செல்க. தற்போது என்ன வடிவம் கிடைத்துள்ளது? அது ஒரு சதுரம். சாய்சதுரத்தின் பரப்பளவு சதுரத்தின் பரப்பளவிற்குச் சமமாக இருக்கும். 

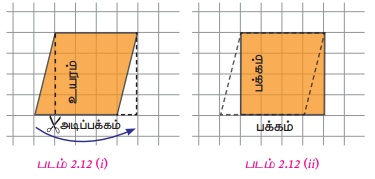
எனவே, சாய்சதுரத்தின் பரப்பளவு = சதுரத்தின் பரப்பளவு

= பக்கம் × பக்கம் ச.அலகுகள் 

= அடிப்பக்கம் × உயரம் ச.அலகுகள்

2. சாய்சதுரத்தின் பரப்பளவு (மூலைவிட்டங்கள் கொடுக்கப்பட்டிருப்பின்)

கொடுக்கப்பட்ட சாய்சதுரம் ABCD யை இரு முக்கோணங்களாகப் பிரித்து, அதன் பரப்பளவைக் காண்போம்.

ABCD என்ற சாய்சதுரத்தில் AB = BC = CD = DA, மூலை விட்டங்கள் AC (d1) மற்றும் BD (d2) ஒன்றுக்கொன்று செங்குத்து ஆகும். 

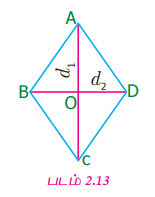
ஆகவே, சாய்சதுரம் ABCD இன் பரப்பளவு = முக்கோணம் ABC ன் பரப்பு + முக்கோணம் ADCன் பரப்பு

= 1/2 × AC × OB + 1/2 × AC × OD

 = 1/2 × AC (OB+OD)

 = 1/2 × AC × BD

 = 1/2 × d1 × d2 ச.அலகுகள்

எனவே, சாய்சதுரத்தின் பரப்பளவு = 1/2 (மூலைவிட்டங்களின் பெருக்கற்பலன்) ச.அலகுகள்.

இவற்றை முயல்க 

1. படம் 2.14 ஐ உற்றுநோக்கி கீழ் உள்ள வினாக்களுக்கு விடையளிக்க.

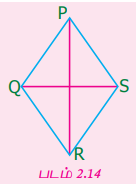
(i) இரண்டு எதிர்ப் பக்கங்களுக்கும் பெயரிடுக. 

இரண்டு எதிர்ப் பக்கங்கள் PQ மற்றும்  RS, QR மற்றும் PS.

(ii) இரண்டு அடுத்துள்ள பக்கங்களுக்கும் பெயரிடுக. 

இரண்டு அடுத்துள்ள பக்கங்கள் PQ மற்றும் QR, PS மற்றும் RS.

(iii) இரண்டு மூலைவிட்டங்களுக்கும் பெயரிடுக.

இரண்டு மூலைவிட்டங்கள் PR மற்றும் QS.

2. படம் 2.15 லும் படம் 2.16 லும் கொடுக்கப்பட்டுள்ள சாய்சதுரத்தின் பரப்பளவு காண்க 

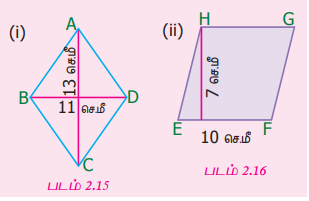
(i) d1 = 11 cm, d2 = 13 cm

சாய்சதுரத்தின் பரப்பளவு = ½ d1 × d2 சதுர.அலகுகள் 

= 1/2 × 11 × 13 சதுர.செமீ 

= 143 / 2 = 71.5 சதுர.செமீ

 (ii) அடிப்படை  b = 10 cm

உயரம்  h = 7 cm

சாய்சதுரத்தின் பரப்பளவு = b × h சதுர.அலகுகள்

= 10 × 7 = 70 துர.செமீ

எடுத்துக்காட்டு 2.6

பக்க அளவு 17 செ.மீ மற்றும் உயரம் 8 செ.மீ கொண்ட சாய்சதுரத்தின் பரப்பளவு காண்க. 

தீர்வு 

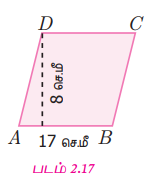
கொடுக்கப்பட்ட அளவுகள் : 

பக்க அளவு = 17 செ.மீ, உயரம் = 8 செ.மீ 

சாய்சதுரத்தின் பரப்பளவு = b × h  ச. அலகுகள்

= 17 × 8 = 136

எனவே, சாய்சதுரத்தின் பரப்பளவு 136 ச.செ.மீ ஆகும்.

சிந்திக்க

1. சாய்சதுரத்தின் சுற்றளவைக் காண முடியுமா? 

2. சாய்சதுரத்தின் மூலைவிட்டங்கள் ஒரே அளவாக இருக்க முடியுமா? 

3. ஒரு சதுரம் சாய்சதுரமானது ஆகும். ஆனால் ஒரு சாய் சதுரம், சதுரம் ஆகாது ஏன்? 

4. மூலை விட்டமும், பக்க அளவும் சமமாக இருக்குமாறு ஒரு சாய்சதுரம் வரைய இயலுமா?

எடுத்துக்காட்டு 2.7

மூலைவிட்டங்கள் 6 செ.மீ, 8 செ.மீ கொண்ட சாய்சதுரத்தின் பரப்பு காண்க. 

தீர்வு 

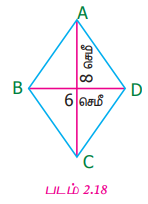
கொடுக்கப்பட்ட அளவுகள்: d1 = 6 செ.மீ, d2 = 8 செ.மீ

சாய்சதுரத்தின் பரப்பு   = 1/2 × (d1 × d2) ச.அலகுகள்

= 1/2 × (6 × 8)

= 48/2

 = 24 ச.செ.மீ 

எனவே, சாய்சதுரத்தின் பரப்பளவு 24 செ.மீ ஆகும். 

எடுத்துக்காட்டு 2.8

ஒரு சாய்சதுரத்தின் பரப்பளவு 60 ச.செ.மீ மற்றும் அதன் ஒரு மூலைவிட்டம் 8 செ.மீ எனில், மற்றொரு மூலைவிட்டத்தைக் காண்க. 

தீர்வு 

கொடுக்கப்பட்ட அளவுகள், மூலைவிட்டம் (d1) = 8 செ.மீ

மூலைவிட்டம் d2    = ? 

சாய்சதுரத்தின் பரப்பளவு = 60 ச.செ.மீ (கொடுக்கப்பட்டுள்ளது)

1/2 × (d1×d2) = 60 

1/2 × (8×d2) = 60

 8×d2 = 60 × 2

d2 = 120/8

= 15

எனவே, மற்றொரு மூலை விட்டத்தின் நீளம் 15 செ.மீ ஆகும்.

எடுத்துக்காட்டு 2.9

ஓர் அலுவலகக் கட்டிடத் தரையில் 200 சாய்சதுர வடிவிலான ஓடுகள் பதிக்கப்பட்டுள்ளன. ஓடுகளின் மூலைவிட்டங்களின் அளவுகள் 40 செ.மீ மற்றும் 25 செ.மீ எனில், தரையை மெருகூட்டச் சதுரமீட்டருக்கு ₹ 45 வீதம் மொத்தச் செலவைக் காண்க.

தீர்வு

சாய்சதுர வடிவிலான ஓடுகளின் மூலைவிட்டங்களின் நீளங்கள் முறையே, 40 செ.மீ மற்றும் 25 செ.மீ எனில், d1 = 40 செ.மீ, d2 = 25 செ.மீ

ஒரு சாய்சதுர வடிவ ஓட்டின் பரப்பளவு = 1/2 × (d1 × d2) ச.அலகுகள்

= 1/2 × 40 × 25

= 500 ச.செ.மீ

எனவே 200 ஓடுகளின் பரப்பளவு = 200 × 500 ச.செ.மீ

= 100000 ச.செ.மீ

= 100000/ 10000 (1 ச.மீ = 10000 ச.செ மீ)

= 10 ச.மீ 

தரையை மெருகூட்ட 1 ச.மீ க்கு ஆகும் செலவு ₹ 45. 

எனவே, மொத்தச்செலவு = 10 × 45 = ₹450.

இரயில்வே மொழியில் டயமண்ட் கிராசிங் (diamond crossing) என்பது இரண்டு இரயில் பாதைகள் ஒன்றோடொன்று கடக்கும் இடமாகும். அப்படிக் கடக்கின்ற இடத்தில் ஒரு சாய்சதுர வடிவம் உருவாகிறது. மிகவும் புகழ்பெற்ற டயமண்ட் கிராசிங் நாக்பூரின் அருகில் அமைந்துள்ளது. அங்குதான் வடக்கு, தெற்கு, கிழக்கு மற்றும் மேற்கு இரயில்வே சந்திப்புகளும் கலக்கின்றன.