பயிற்சி 2.4

பயிற்சி 2.4 

பல்வகை திறனறி பயிற்சிக் கணக்குகள் 

1. ஓர் இணைகரத்தின் அடிப்பக்கம் 16 செ.மீ. அதன் உயரம் அடிப்பக்கத்தை விட 7 செ.மீ குறைவு எனில், அதன் பரப்பளவைக் காண்க. 

தீர்வு : 

கொடுக்கப்பட்டவை b = 16 செ.மீ, h = 9 செ.மீ 

இணைகரத்தின் பரப்பு = bh ச.அ

= 16 × 9 

= 144 செ.மீ2 

h = b - 7 செ.மீ 

2. ஓர் இணைகர வடிவ விவசாய நிலத்தின் பரப்பளவு 68.75 ச. ஹெக்டோ மீ. அதன் இணைப்பக்கங்களுக்கு இடையேயுள்ள தொலைவு 6.25 ஹெக்டோ மீ எனில், அதன் அடிப்பக்க அளவைக் காண்க. 

தீர்வு : 

கொடுக்கப்பட்டவை பரப்பு = 68.75 ச. ஹெக்டோ மீ, h = 6.25 ஹெ.மீ 

இணைகரத்தின் பரப்பு = bh ச.அ

b × h = 16 × 9 

b × 6.25 = 68.75

b = 68.75 / 6.25

b = 11 ஹெ.மீ 

3. 48 மீ பக்க அளவு கொண்ட ஒரு சதுரமும், 18 மீ உயரம் கொண்ட ஒரு இணைகரமும் சமப் பரப்பளவைக் கொண்டவை எனில், இணைகரத்தின் அடிப்பக்க அளவைக் காண்க. 

தீர்வு : 

கொடுக்கப்பட்டவை a = 48 மீ, h = 18 மீ 

இணைகரத்தின் பரப்பு = சதுரத்தின் பரப்பு

b × h = 2304 

b × 18 = 2304

b = 2304 / 18

b = 128 மீ 

4. 676 ச.செ.மீ பரப்பளவு கொண்ட ஓர் இணைகரத்தின் உயரம் அதன் அடிப்பக்கத்தில் 4ல் ஒரு பங்கு எனில், அதன் அடிப்பக்கத்தின் அளவையும், உயரத்தையும் காண்க. 

தீர்வு : 

கொடுக்கப்பட்டவை b = x செ.மீ , h = x / 4 செ.மீ 

இணைகரத்தின் பரப்பு = 676 செ.மீ2

bh = 676 

x × x / 4 = = 676 

x2 = 676 × 4 

x2 = 2704 

x = 52 செ.மீ

h × x / 4 = 52 / 4

= 13

h = 13 செ.மீ

5. ஒரு சாய்சதுரத்தின் பரப்பளவு 576 ச.செ.மீ ஓர் மூலைவிட்டமானது மற்றொரு மூலைவிட்டத்தில் பாதி எனில், மூலைவிட்டங்களின் அளவுகளைக் காண்க. 

தீர்வு : 

கொடுக்கப்பட்டவை சாய்சதுரத்தின் பரப்பு = 576 ச.செ.மீ d1 = x செ.மீ, d2 = x / 2 செ.மீ.

பரப்பு = 1/2 × d 1× d2 ச.அ

1/2 × d 1× d2 = 576 

1/2 × x × x/2 = 576

x2 = 576 × 4 

x2 = 2304

x = 48 செ.மீ 

d1 = x = 48 செ.மீ 

d1 = 48 செ.மீ

d2 = x / 2 = 48 / 2 = 24 செ.மீ 

d2 = 24 செ.மீ

6. ஓர் இருசமபக்கச் சரிவகம் வடிவில் உள்ள மைதானத்தின் இணைப் பக்கங்கள் 42மீ மற்றும் 36மீ இணைப்பக்கங்களுக்கு இடையேயுள்ள தொலைவு (உயரம்) 30 மீ எனில், அந்த மைதானத்தைச் சமப்படுத்த ஒரு ச.மீக்கு ₹135 வீதம் எவ்வளவு செலவு ஆகும்? 

தீர்வு : 

கொடுக்கப்பட்டவை, a = 42 மீ, b = 36 மீ, h = 30 மீ. 

சரிவகத்தின் பரப்பு = 1/2 × h × (a + b) ச.அ

= 1/2 × 30 × (42 + 36) 

= 15 × 78

= 1170 மீ2 

மைதானத்தை சமப்படுத்த ஒரு ச.மீ க்கு = 135 

மைதானத்தை சமப்படுத்த 1170 ச.மீக்கு = 135 × 1170

= 1,57,950

மேற்சிந்தனைக் கணக்குகள் 

7. PQRS என்பது ஓர் இணைகரம் (படத்தைக் கவனிக்க). பக்கம் QR இன் உயரம் PM, பக்கம் RS இன் உயரம் PN. இணைகரத்தின் பரப்பளவு 900 ச.செ.மீ, PM மற்றும் PN இன் அளவுகள் முறையே 20 செ.மீ, 36 செ.மீ எனில், பக்கம் QR மற்றும் RS இன் அளவைக் காண்க.

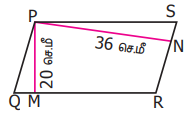
தீர்வு : 

கொடுக்கப்பட்டவை பரப்பு = 900 செ.மீ2, h1 = 20 செ.மீ, h2 = 36 செ.மீ

இணைகரத்தின் பரப்பு = b1 h1 ச.அ  

b1 h1 = 900 

b1 × 20 = 900

b1 = 900 / 20

b1 = 45 செ.மீ

இணைகரத்தின் பரப்பு = b2 h2 ச.அ

b2 h2 = 900 

b2 × 36 = 900 

b2 = 900 / 30

b2 = 25 செ.மீ 

QR = 45 செ.மீ

SR = 25 செ.மீ

8. ஓர் இணைகரத்தின் அடிப்பக்கமும் உயரமும் 7 : 3 என்ற விகிதத்தில் உள்ளன. அதன் உயரம் 45 செ.மீ எனில், அதன் பரப்பளவைக் காண்க. 

தீர்வு:

கொடுக்கப்பட்டவை b : h = 7:3, h = 45 செ.மீ 

= b / h = (7 / 3) b = 7h / 3 = (7 × 45) / 3 

b = 105 செ.மீ 

இணைகரத்தின் பரப்பு = bh ச.அ

= 45 × 105 

= 4725 செ.மீ2

9. AC = 24 செ.மீ, BE = DF = 8 செ.மீ எனில், படத்தில் உள்ள ABCD என்ற இணைகரத்தின் பரப்பளவைக் காண்க. 

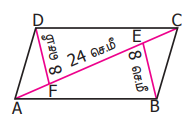
தீர்வு : 

கொடுக்கப்பட்டவை b = 24 செ.மீ, h = 8 செ.மீ 

இணைகரத்தின் பரப்பு = bh ச.அ 

= 24 × 8

= 192 செ.மீ2

10. படத்தில் காட்டியுள்ள ABCD என்ற இணைகரத்தின் பரப்பளவு 1470 ச.செ.மீ. AB = 49 செ.மீ AD = 35 செ.மீ எனில், BE மற்றும் DF அகியவற்றின் அளவைக் காண்க. 

தீர்வு:

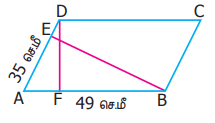
கொடுக்கப்பட்டவை b1 = 49 செ.மீ, b2 = 35 செ.மீ, 

h1 = ?  h2 = ?

இணைகரத்தின் பரப்பு = bh ச.அ

b1 × h1 = 1470 

49 × h1 =1470

h1 = 1470 / 49 

h1 = 30 செ.மீ  DF = 30 செ.மீ 

இணைகரத்தின் பரப்பு = bh ச.அ

b2 × h2 = 1470 

35 × h2 = 1470

h2 = 1470 / 35 

h2 = 42 செ.மீ

BE = 42 செ.மீ

11. ஒரு சாய்சதுரத்தின் மூலைவிட்ட அளவுகளின் கூடுதல் 24 மீ பெரிய மூலைவிட்டத்தின் அளவு சிறிய மூலைவிட்ட அளவைப் போல மூன்று மடங்கு எனில் அதன் பரப்பளவைக் காண்க.

தீர்வு : 

கொடுக்கப்பட்டவை d1 = x செ.மீ, d2 = 3𝓍 செ.மீ

d1 + d2 = 24 

𝓍 + 3 𝓍 = 24

4 𝓍 = 24 ⇒ 𝓍 = 6 செ.மீ

d1 = 6 செ.மீ 

d2 = 18 செ.மீ 

சாய்சதுரத்தின் பரப்பு = 1/2 × d1 × d2 ச.அ

= 1/2 × 6 × 18 

= 54 ச.செ.மீ

12. ஒருவர் சாய்சதுர வடிவிலான நீச்சல் குளம் ஒன்றை அமைக்க விரும்புகிறார். அதன் ஒரு மூலைவிட்ட அளவானது 13 மீ. மற்றொரு மூலைவிட்ட அளவு இதைப் போல இரண்டு மடங்கு எனில், நீச்சல் குளத்தின் பரப்பளவைக் காண்க. மேலும் அதன் தரையை மெருகூட்ட செ.மீக்கு ₹15 வீதம் மொத்தச் செலவைக் காண்க. 

தீர்வு : 

கொடுக்கப்பட்டவை d1 = 13 செ.மீ, d2 = 26 செ.மீ

சாய்சதுரத்தின் பரப்பு = 1/2 × d1 × d2 ச.அ

= 1/2 × 13 × 26

=169 ச.செ.மீ 

தரையை மெருகூட்ட 1 ச.செ.மீ க்கு = ₹15 

தரையை மெருகூட்ட 169 ச.செ.மீக்கு = ₹169 × 15

= ₹ 2535.

13. பரப்பளவு 576 ச.செ.மீ உம், உயரத்தைப்போல் நான்கு மடங்கு கொண்ட அடிப்பக்கத்தையும் உடைய இணைகரத்தின் உயரம் காண்க. 

தீர்வு : 

கொடுக்கப்பட்டவை h = x செ.மீ, b = 4x செ.மீ 

இணைகரத்தின் பரப்பு = bh ச.அ

bh = 576 

x × 4x = 576 

x2 = 576 / 4

x2 = 144

x = 12 செ.மீ

h  = 12 செ.மீ

b = 4, x = 4 × 12  

b = 48 செ.மீ

14. ஒரு மேஜையின் மேற்பரப்பு சரிவக வடிவில் உள்ளது. அதன் அளவுகள் படத்தில் கொடுக்கப்பட்டுள்ளன. அதன் மேற்பரப்பு மீது கண்ணாடி பொருத்த 10 ச.செ.மீக்கு ₹6 வீதம் எவ்வளவு செலவு ஆகும்? 

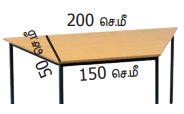
தீர்வு : 

கொடுக்கப்பட்டவை a = 200 செ.மீ, b = 150 செ.மீ, h = 50 செ.மீ 

சரிவகத்தின் பரப்பு = 1/2 × h × (a + b) ச.அ

= 1/2 × 50 × (200 + 150) 

= 25 × 350

= 8750 ச.செ.மீ 

கண்ணாடி பொருத்த 10 ச.செ.மீக்கு = ₹ 15 

கண்ணாடி பொருத்த 8750 ச.செ.மீக்கு = ₹ 875 × 6

= ₹ 5,250. 

15. அறிவு என்பவருக்குச் சொந்தமான ABCD என்ற நிலம் படத்தில் கொடுக்கப்பட்ட அளவுகள் கொண்டது. அதில் ABED என்ற பகுதி மட்டும் விளைச்சலுக்குப் பயன்பாட்டில் உள்ளது. (E என்பது CD யின் மையப்புள்ளி ஆகும்.) விளைச்சல் நிலத்தின் பரப்பளவைக் காண்க. 

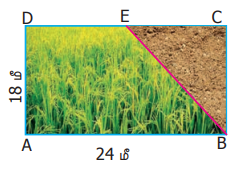
தீர்வு :

கொடுக்கப்பட்டவை AB = 24 மீ, AD = 18 மீ, EC = 12 மீ 

செவ்வகத்தின் பரப்பு = lb ச.அ

= 24 × 18 

= 432 ச.மீ

முக்கோணத்தின் பரப்பு = 1/2 × b × h ச.அ

= 1/2 × 12 × 18 

= 6 × 18

= 108 ச.மீ 

விளைச்சல் நிலத்தின் பரப்பு = செவ்வகத்தின் பரப்பு - முக்கோணத்தின் பரப்பு

= 432 - 108 

= 342 மீ2 (அ) ச.மீ.

விடைகள் 

பயிற்சி  2.4

1. 144 செ.மீ2 

2. 11 ஹெ.மீ

3. 128 மீ

4. h = 13 செ.மீ b = 52செ.மீ

5. d1 = 48 செ.மீ d2 = 24செ.மீ

6. ₹ 1,57,950

மேற்சிந்தனைக் கணக்குகள் 

7. 45 செ.மீ; 25 செ.மீ

8. 4725 செ.மீ2

 9. 192 செ.மீ2

10. DF = 30செ.மீ BE = 42செ.மீ

11. 54 ச.செ.மீ

12. 169 ச.செ.மீ; ₹ 2535

13. 12 செ.மீ

14. ₹ 5250

15. 342 மீ2 (அ) ச.மீ.