ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகள்

ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகள் (Conservative force and Non Conservative force) 

ஆற்றல் மாற்றா விசை (Conservative Force) 

ஒரு பொருளை நகர்த்தும் போது விசையினால் அல்லது விசைக்கெதிராக செய்யப்பட்ட வேலை பொருளின் தொடக்க மற்றும் இறுதி நிலைகளை மட்டும் சார்ந்தும், பொருளின் தொடக்க மற்றும் இறுதி நிலைகளுக்கிடையே சென்ற பாதையின் இயல்பைச் சாராமலும் இருப்பின்; அவ்விசை, ஆற்றல் மாற்றா விசை எனப்படும்.

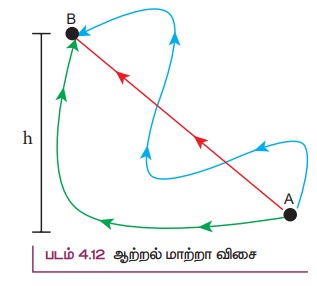
புவியில் A என்ற புள்ளியில் உள்ள ஒரு பொருளைக் கருதுவோம். படம் 412இல் காட்டியுள்ளவாறு இதனை h உயரத்தில் உள்ள B என்ற மற்றொரு புள்ளிக்கு மூன்று பாதைகளில் எடுத்துச் செல்லலாம்.

பாதை எவ்வாறு இருப்பினும் தொடக்க மற்றும் இறுதி நிலைகள் மாறாமல் இருக்கும் வரை புவியீர்ப்பு விசைக்கெதிராக செய்யப்பட்ட வேலை மாறாது. இதுவே புவியீர்ப்பு விசையானது ஆற்றல் மாற்றா விசையாக இருப்பதற்கு காரணமாகும். ஆற்றல் மாற்றா விசை நிலை ஆற்றலின் எதிர்க்குறி சாய்வுக்கு சமமாகும்.

ஒரு பரிமாண நேர்வில்

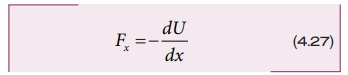
மீட்சி சுருள்வில் விசை, நிலைமின்னியல் விசை, காந்த விசை, புவியீர்ப்பு விசை போன்றவை ஆற்றல் மாற்றா விசைகளுக்கு உதாரணங்கள் ஆகும்.

ஆற்றல் மாற்றும் விசை (Non - Conservative Force) 

ஒரு பொருளை விசையினால் அல்லது விசைக்கெதிராக நகர்த்தச் செய்யப்பட்ட வேலை தொடக்க மற்றும் இறுதி நிலைகளுக்கிடையே உள்ள பாதையைச் சார்ந்திருப்பின் அவ்விசை ஆற்றல் மாற்றும் விசை எனப்படும். இதன் பொருள் வேவ்வேறு பாதைகளில் செய்யப்பட்ட வேலையின் மதிப்பு மாறுபடும் என்பதாகும். 

1. உராய்வு விசைகள் ஆற்றல் மாற்றும் விசைகள் ஆகும். ஏனென்றால் உராய்வுக்கு எதிராக செய்யப்பட்ட வேலை பொருள் நகர்ந்த பாதையின் தொலைவைச் சார்ந்தது. 

2. காற்றுத்தடையால் ஏற்படும் விசை, பாகியல் விசை ஆகியவையும் ஆற்றல் மாற்றும் விசைகள் ஆகும். இவ்விசையால் அல்லது விசைக்கெதிராக செய்யப்பட்ட வேலை இயக்கத்தின் திசைவேகத்தைச் சார்ந்தது.

ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகளின் பண்புகள் அட்டவணை 4.3இல் தொகுக்கப்பட்டுள்ளன.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகள்

எடுத்துக்காட்டு 4.11

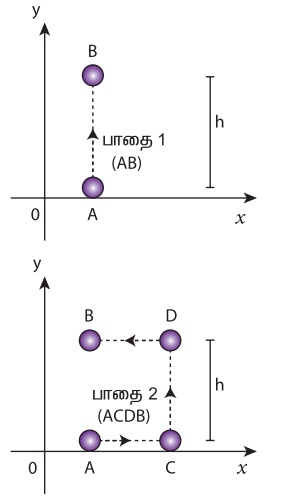
கீழ்கண்ட நேர்வுகளில் புவியீர்ப்பு விசையினால் செய்யப்பட்ட வேலையைக் கணக்கிடுக.

தீர்வு

விசை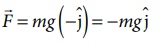

இடப்பெயர்ச்சி வெக்டர்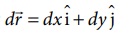

(இடப்பெயர்ச்சி இரு பரிமாணத்தில் உள்ளதால் அலகு வெக்டர்கள் மற்றும் பயன்படுத்தப்படுகிறது)

(a) இயக்கமானது செங்குத்தாக மட்டும் உள்ளதால், இடப்பெயர்ச்சியின் கிடைத்தளக்கூறு dx சுழியாகும். எனவே பாதை 1 இன் வழியே விசையினால் செய்யப்பட்ட வேலை (h தொலைவிற்கு)

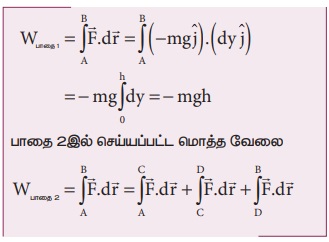
ஆனால்

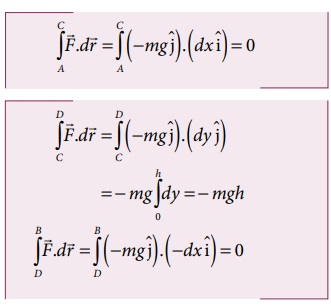
எனவே பாதை 2 இன் வழியே விசையினால் செய்யப்பட்ட மொத்த வேலை

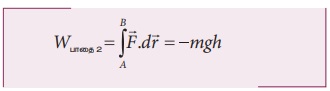
ஆற்றல் மாற்றா விசையினால் செய்யப்பட்ட வேலை பாதையைச் சார்ந்ததல்ல என்பதை அறியவும்.

எடுத்துக்காட்டு 4.12

2 kg நிறையுள்ள ஒரு பொருள் இயக்க உராய்வுக் குணகம் 0.9 கொண்டுள்ள ஒரு பரப்பில் 20 N புறவிசையினால் 10 m தொலைவிற்கு நகர்த்தப்படுவதாகக் கருதுக. புறவிசை மற்றும் இயக்க உராய்வினால் செய்யப்பட்ட வேலை என்ன? முடிவைப் பற்றிய கருத்தைக் கூறுக (g = 10 ms-2 எனக் கொள்க)

தீர்வு

m = 2 kg, d = 10 m, Fext = 20 N, µk = 0.9 

ஒரு பொருள் கிடைமட்டப் பரப்பில் இயங்கும்போது அது இரு விசைகளைப் பெறுகிறது. 

(a) புற விசை Fext = 20 N 

(b) இயக்க உராய்வு விசை

fk = μk mg = 0.9 × (2) × 10 = 18N. 

புறவிசையினால் செய்யப்பட்ட வேலை

Wext = Fd = 20 × 10 = 200 J 

இயக்க உராய்வு விசையினால் செய்யப்பட்ட வேலை 

Wk = fkd = (-18) × 10 = -180 J

இங்கு எதிர்க்குறியானது இயக்க உராய்வு விசை, இடப்பெயர்ச்சியின் திசைக்கு எதிராக உள்ளதைக் குறிக்கிறது.

பொருளின் மீது செய்யப்பட்ட மொத்த வேலை 

Wtotal = Wext + Wk = 200 - 180 = 20 J 

உராய்வு விசை ஒரு ஆற்றல் மாற்றும் விசை என்பதால் புறவிசையால் கொடுக்கப்பட்ட 200 J இல் 180 J இழக்கப்பட்டது மற்றும் இதனை மீட்டெடுக்க இயலாது.