11வது இயற்பியல் : அலகு 4 : வேலை, ஆற்றல் மற்றும் திறன்
ஆற்றல்
ஆற்றல் (ENERGY)
ஆற்றல் என்பது வேலை செய்யும் திறமையே ஆகும். அதாவது, செய்யப்பட்ட வேலை என்பது ஆற்றலின் செயல்பாடே ஆகும். அதனால் தான் வேலை மற்றும் ஆற்றல் இரண்டும் ஒரே பரிமாணத்தைக் கொண்டுள்ளன (ML2T-2).

ஆற்றலின் முக்கியமான அம்சம் யாதெனில் ஒரு தனித்த அமைப்பிற்கு அனைத்து வகை ஆற்றல்களின் கூடுதல், அதாவது மொத்த ஆற்றலானது எந்தச் செயல்பாட்டிலும் எவ்வகையான அகமாற்றங்கள் ஏற்பட்டாலும் மாறாமல் இருக்கும். இதன் பொருளானது ஒரு வடிவில் மறையும் ஆற்றல் மற்றொரு வடிவில் வெளிப்படும். இதுவே ஆற்றல் மாறா விதி எனப்படும். இப்பாடப்பகுதியில் நாம் இயந்திர ஆற்றல் பற்றி மட்டும் கற்போம்.
இயந்திர ஆற்றல் இரு வகைப்படும்.
1. இயக்க ஆற்றல்
2. நிலை ஆற்றல்
ஒரு பொருள் தனது இயக்கத்தினால் கொண்டுள்ள ஆற்றல் இயக்க ஆற்றல் எனப்படும். ஒரு பொருள் தனது நிலைப்பாட்டினால் கொண்டுள்ள ஆற்றல் நிலை ஆற்றல் ஆகும்.
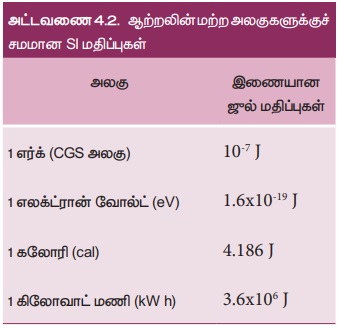
ஆற்றலின் SI அலகானது செய்யப்பட்ட வேலையின் அலகே ஆகும். அதாவது N m (அல்லது) ஜுல் (J). ஆற்றலின் பரிமாணம், செய்யப்பட்ட வேலையின் பரிமாணமே ஆகும். அதன் பரிமாணம் [ML2T-2] ஆகும். ஆற்றலின் வேறு அலகுகள் மற்றும் அவற்றின் SI மதிப்புகள் அட்டவணை 4.2 இல் காண்பிக்கப்பட்டுள்ளன.
இயக்க ஆற்றல் [Kinetic Energy]
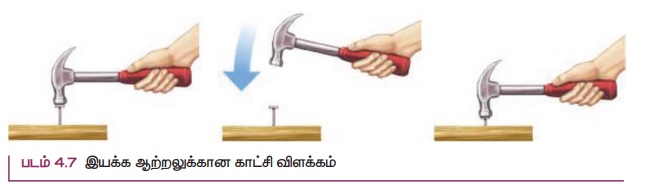
இயக்க ஆற்றல் என்பது ஒரு பொருள் அதன் இயக்கத்தால் பெற்றுள்ள ஆற்றலாகும். அனைத்து இயங்கும் பொருட்களும் இயக்க ஆற்றலைக் கொண்டுள்ளன. இயக்கத்தில் உள்ள ஒரு பொருள் வேலை செய்வதற்கான திறமையைப் பெற்றிருக்கும். உதாரணமாக, ஒரு ஆணியின் மீது ஓய்வு நிலையில் வைக்கப்பட்ட ஒரு சுத்தியல் ஆணியை மரத்தினுள் செலுத்தாது. அதேசமயம் படம் 4.7 இல் காட்டியவாறு அந்த சுத்தியலால் ஆணியை அடிக்கும் போது அது ஆணியை மரத்தினுள் செலுத்துகிறது. ஒரு பொருள் இயங்கும் போது, இயக்கத்திற்காக செய்யப்படும் வேலையின் அளவாக இயக்க ஆற்றல் அளவிடப்படுகிறது. இயங்கும் பொருளின் இயக்கத்திற்காக செய்யப்பட்ட வேலையின் அளவானது பொருளின் நிறை மற்றும் திசைவேகத்தின் எண்மதிப்பு ஆகியவற்றைச் சார்ந்தது. இயக்கத்தில் இல்லாத ஒரு பொருள் இயக்க ஆற்றலைக் கொண்டிருக்காது.
வேலை-இயக்க ஆற்றல் தேற்றம்
வேலையும் ஆற்றலும் சமமானவை. இது இயக்க ஆற்றலுக்கும் பொருந்தும். இதனை நிரூபிக்க m நிறையுள்ள ஒரு பொருள் உராய்வற்ற கிடைத்தளப் பரப்பில் ஓய்வில் இருப்பதாகக் கருதுவோம்
(F) என்ற மாறா விசையினால் அதே திசையில் (s) என்ற இடப்பெயர்ச்சியை ஏற்படுத்த செய்யப்பட்ட வேலை
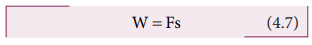
மாறாத விசைக்கான சமன்பாடு,
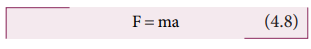
மூன்றாவது இயக்கச் சமன்பாட்டை (பகுதி 2.10.3 ஐக் காண்க) இவ்வாறு எழுதலாம்.
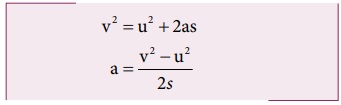
a இன் மதிப்பை சமன்பாடு 4.8 இல் பிரதியிட
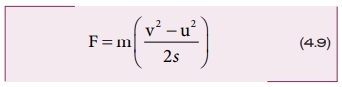
சமன்பாடு 4.9 ஐ 4.7 இல் பிரதியிட,
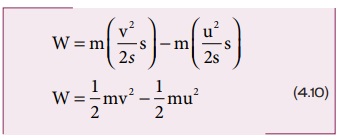
இயக்க ஆற்றலுக்கான கோவை:
மேற்கண்ட சமன்பாட்டில் (1/2 mv2) என்பது என்பது (v) திசைவேகத்தில் இயங்கும் (m) நிறையுள்ள பொருளின் இயக்க ஆற்றலைக் குறிக்கும்.
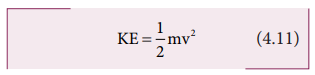
பொருளின் இயக்க ஆற்றல் எப்பொழுதும் நேர்க்குறி மதிப்புடையதாகும்.
சமன்பாடு (4.10) மற்றும் (4.11) இல் இருந்து
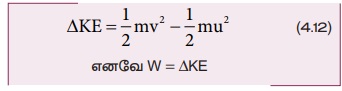
சமன்பாடு 4.12 இல் வலது பக்கத்தில் உள்ள கோவை பொருளின் இயக்க ஆற்றல் மாறுபாடு (ΔKE) ஆகும்.
பொருளின் மீது விசையினால் செய்யப்பட்ட வேலை பொருளின் இயக்க ஆற்றலை மாற்றுகிறது என்பதை இது குறிக்கிறது. இதுவே வேலை - இயக்க ஆற்றல் தேற்றம் எனப்படும்.
வேலை - இயக்க ஆற்றல் தேற்றமானது கீழ்க்காண்பவற்றை உணர்த்துகிறது.
1. பொருளின் மீது விசையினால் செய்யப்பட்ட வேலை நேர்க்குறியாக இருந்தால் அதன் இயக்க ஆற்றல் அதிகரிக்கிறது.
2. பொருளின் மீது விசையினால் செய்யப்பட்ட வேலை எதிர்க்குறியாக இருந்தால் அதன் இயக்க ஆற்றல் குறைகிறது.
3. பொருளின் மீது விசையினால் வேலை ஏதும் செய்யப்பட வில்லை எனில் அதன் இயக்க ஆற்றல் மாறாது. இது, பொருளின் நிறை மாறாத போது விசையினால் பொருளானது மாறா வேகத்தில் இயங்கியது என்பதைக் குறிக்கிறது.
உந்தம் மற்றும் இயக்க ஆற்றல் இடையே உள்ள தொடர்பு
m நிறையுள்ள ஒரு பொருள் ![]() என்ற திசைவேகத்தில் இயங்குவதாகக் கருதுவோம். அதன் நேர்கோட்டு உந்தம்
என்ற திசைவேகத்தில் இயங்குவதாகக் கருதுவோம். அதன் நேர்கோட்டு உந்தம் 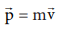 மற்றும் அதன் இயக்க ஆற்றல், KE = ½ mv2
மற்றும் அதன் இயக்க ஆற்றல், KE = ½ mv2
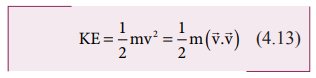
சமன்பாடு 4.13 இன் தொகுதி மற்றும் பகுதியை நிறை m ஆல் பெருக்க

இங்கு ![]() என்பது உந்தத்தின் எண் மதிப்பாகும். நேர்கோட்டு உந்தத்தின் எண் மதிப்பை இவ்வாறு பெறலாம்.
என்பது உந்தத்தின் எண் மதிப்பாகும். நேர்கோட்டு உந்தத்தின் எண் மதிப்பை இவ்வாறு பெறலாம்.
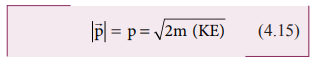
இயக்க ஆற்றல் மற்றும் நிறை கொடுக்கப்பட்டால் உந்தத்தின் எண் மதிப்பை மட்டுமே கணக்கிட இயலும். ஆனால் உந்தத்தின் திசையைக் கணக்கிட இயலாது என்பதை அறியவும். ஏனென்றால் இயக்க ஆற்றல் மற்றும் நிறை ஆகியவை ஸ்கேலர் அளவுகளாகும்.
நிலை ஆற்றல் [Potential Energy]
ஒரு பொருளின் நிலை ஆற்றல் என்பது சுற்றுப்புறத்தைப் பொறுத்து அதன் நிலை மற்றும் அமைப்பைச் சார்ந்தது. ஏனென்றால் பொருளின் மீது செயல்படும் பல்வேறு விசைகளும் அதன் நிலை மற்றும் அமைப்பைச் சார்ந்ததே.
P என்ற புள்ளியில் உள்ள ஒரு பொருளின் நிலை ஆற்றல் என்பது அப்பொருளை ஒரு தொடக்க நிலைப் புள்ளி O (தொடக்க நிலை) முதல் புள்ளி P (இறுதிநிலை) வரை மாறா திசைவேகத்தில் நகர்த்த புறவிசையால் செய்யப்பட்ட வேலையின் அளவு என வரையறுக்கப்படுகிறது. O என்ற தொடக்கப் புள்ளியில் நிலை ஆற்றலை சுழி என எடுத்துக் கொள்ளலாம்.
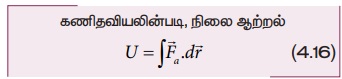
இங்கு தொகையீட்டின் எல்லை (limit) தொடக்க நிலைப்புள்ளி O முதல் இறுதி நிலைப்புள்ளி P வரை அமையும்.
நிலை ஆற்றல் பலவகைப்படும். ஒவ்வொரு வகையும் ஒரு குறிப்பிட்ட விசையுடன் தொடர்புடையது. உதாரணமாக
(i) புவிஈர்ப்பு விசையினால் பொருள் பெற்றுள்ள ஆற்றலானது ஈர்ப்பு அழுத்த ஆற்றல் ஆகும்.
(ii) சுருள்வில் விசை மற்றும் இதுபோன்ற ஒத்த விசைகளினால் பெறப்படும் ஆற்றலானது மீட்சியழுத்த ஆற்றல் ஆகும்.
(iii) நிலை மின்னியல் விசையால் பெறப்படும் ஆற்றல் மின்னழுத்த ஆற்றல் ஆகும்.
ஆற்றல் மாற்றா விசைகளைப் பற்றி பாடப்பகுதி 4.2.7 இல் மேலும் விரிவாகக் காணலாம். தற்போது நாம் ஈர்ப்பு அழுத்த ஆற்றல் மற்றும் மீட்சியழுத்த ஆற்றல் பற்றி விரிவாக விவாதிக்கலாம்.
புவிப்பரப்பிற்கு அருகில் நிலை ஆற்றல்
புவியிலிருந்தும் h உயரத்தில் ஈர்ப்பு அழுத்த ஆற்றல் (U) என்பது பொருளை தரையிலிருந்து h உயரத்திற்கு மாறா திசைவேகத்தில் கொண்டு செல்லத் தேவையான வேலையின் அளவுக்குச் சமமாகும்.
படம் 4.8 இல் (m) நிறையுள்ள ஒரு பொருள் தரையிலிருந்து h உயரத்திற்கு புவியீர்ப்பு விசைக்கு எதிராக நகர்த்தப்படுவதாகக் கருதுவோம்.
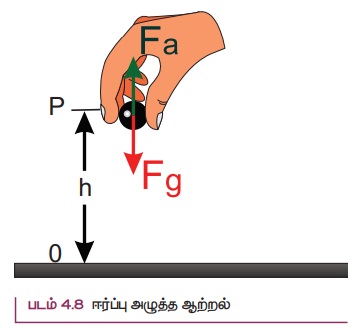
பொருளின் மீது செயல்படும் புவிஈர்ப்பு விசை (![]() g) ஆனது
g) ஆனது ![]() g = - mg jˆ (விசையானது y திசையில் உள்ளதால் அலகு வெக்டர் ˆj இங்கு பயன்படுத்தப்படுகிறது). இங்கு எதிர்க்குறியானது விசை செங்குத்தாக கீழ்நோக்கி செயல்படுவதைக் குறிக்கிறது. பொருளை முடுக்கம் இன்றி (மாறா திசைவேகத்துடன்) நகர்த்த, புவிஈர்ப்பு விசை (
g = - mg jˆ (விசையானது y திசையில் உள்ளதால் அலகு வெக்டர் ˆj இங்கு பயன்படுத்தப்படுகிறது). இங்கு எதிர்க்குறியானது விசை செங்குத்தாக கீழ்நோக்கி செயல்படுவதைக் குறிக்கிறது. பொருளை முடுக்கம் இன்றி (மாறா திசைவேகத்துடன்) நகர்த்த, புவிஈர்ப்பு விசை (![]() g) க்கு சமமான எண் மதிப்பையும் எதிர்திசையையும் கொண்ட (
g) க்கு சமமான எண் மதிப்பையும் எதிர்திசையையும் கொண்ட (![]() a) என்ற புறவிசை ஒன்று பொருளின் மீது செயல்படுத்தப்பட வேண்டும். அதாவது (
a) என்ற புறவிசை ஒன்று பொருளின் மீது செயல்படுத்தப்பட வேண்டும். அதாவது (![]() a = -
a = - ![]() g). இது
g). இது ![]() a = + mg jˆ என்பதைக் குறிக்கிறது. நேர்க்குறியானது செயல்படுத்தப்பட்ட விசை மேல்நோக்கி செங்குத்தாக உள்ளது என்பதைக் குறிக்கிறது. எனவெ பொருள் மேல்நோக்கி உயர்த்தப்படும் போது அதன் திசைவேகம் மாறாமல் இருக்கும், அதனால் அதன் இயக்க ஆற்றலும் மாறாது. ‘h’ உயரத்தில் ஈர்ப்பு அழுத்த ஆற்றல் (U) என்பது பொருளை தரையிலிருந்து (h) உயரத்திற்கு கொண்டு செல்லத் தேவையான வேலையின் அளவாகும்.
a = + mg jˆ என்பதைக் குறிக்கிறது. நேர்க்குறியானது செயல்படுத்தப்பட்ட விசை மேல்நோக்கி செங்குத்தாக உள்ளது என்பதைக் குறிக்கிறது. எனவெ பொருள் மேல்நோக்கி உயர்த்தப்படும் போது அதன் திசைவேகம் மாறாமல் இருக்கும், அதனால் அதன் இயக்க ஆற்றலும் மாறாது. ‘h’ உயரத்தில் ஈர்ப்பு அழுத்த ஆற்றல் (U) என்பது பொருளை தரையிலிருந்து (h) உயரத்திற்கு கொண்டு செல்லத் தேவையான வேலையின் அளவாகும்.
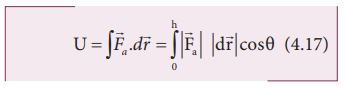
இடப்பெயர்ச்சியும் செயல்படுத்தப்பட்ட விசையும் அதே மேல்நோக்கிய திசையில் உள்ளதால் அவற்றிற்கிடையே உள்ள கோணம், θ = 0° எனவே cos 0° = 1 மற்றும் |![]() a| = mg, |d
a| = mg, |d![]() | = dr
| = dr
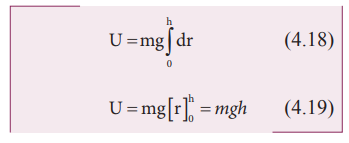
பொருளில் சேமிக்கப்பட்டுள்ள நிலையாற்றலானது புறவிசையினால் செய்யப்பட்ட நேர்க்குறி மதிப்புள்ள வேலையின் மூலம் வரையறுக்கப்படுகிறது என்பதை அறியவும். இயல்பாக இது குறிப்பது யாதெனில் புறவிசையைச் செயல்படுத்தும் அமைப்பு பொருளுக்கு ஆற்றலை மாற்றுகிறது மற்றும் அது நிலையாற்றலாகச் சேமிக்கப்படுகிறது. பொருளானது h உயரத்திலிருந்து விழுந்தால் சேமிக்கப்பட்டுள்ள நிலையாற்றல் இயக்க ஆற்றலாக மாற்றப்படுகிறது.
• ஒரு பொருளின்மீது புறவிசை செயல்படும்போது அப்பொருள் எவ்வாறு சுழிமுடுக்கத்துடன் (மாறா திசைவேகத்தில்) இயங்கும்?
செயல்படுத்தப்படும் புறவிசைக்கு சரியாக எதிர்திசையில் மற்றொரு விசை செயல்பட்டால் இது சாத்தியமே. அவை இரண்டும் சமமான எண்மதிப்பைக் கொண்டு, ஒன்றுக்கொன்று எதிர் திசையில் செயல்படுவதால், பொருளின் மீது செயல்படும் நிகரவிசைசுழியாகும்.எனவே பொருளானது சுழி முடுக்கத்துடன் இயங்கும்.
• நாம் நிலையாற்றலை வரையறை செய்யும்போது பொருளானது ஏன் மாறா திசைவேகத்தில் நகர்த்தப்பட வேண்டும்?
பொருளானது மாறா திசைவேகத்தில் நகரவில்லை என்றால் அது தொடக்க மற்றும் இறுதி நிலைகளில் மாறுபட்ட திசைவேகங்களைக் கொண்டிருக்கும். வேலை – இயக்க ஆற்றல் தேற்றப்படி புறவிசையானது கூடுதலாக இயக்க ஆற்றலைச் செலுத்தும். ஆனால் நாம் நிலையாற்றலை புவியீர்ப்பு விசை, சுருள்வில் விசை மற்றும் கூலும் விசை போன்ற விசைகளுக்கு வரையறுத்துள்ளோம். எனவே பொருளை தொடக்க நிலை முதல் இறுதிநிலை வரை நகர்த்தும்போது புற அமைப்பு (புற விசை) எந்த இயக்க ஆற்றலையும் செலுத்தக்கூடாது.
மீட்சி நிலை ஆற்றல் (Elastic Potential Energy]
ஒரு சுருள்வில் நீட்சியடையச் செய்யப்பட்டால் அதனுள் ஒரு மீள்விசை உருவாகிறது. சுருள்வில்லை நீட்சிக்கக்கூடிய அல்லது அமுக்கக்கூடிய விசையினால் சுருள்வில் பெற்றுள்ள நிலை ஆற்றல் மீட்சி நிலை ஆற்றல் எனப்படும். மீள் விசைக்கு எதிராகச் செயல்படுத்தப்பட்ட விசையினால் செய்யப்பட்ட வேலை சுருள்வில்லில் மீட்சி நிலை ஆற்றலாகச் சேமிக்கப்படுகிறது.
ஒரு சுருள்வில் - நிறை அமைப்பைக் கருதுக. படம் 4.9 இல் காட்டியவாறு உராய்வற்ற கிடைத்தள மேசையில் m என்ற நிறை வைக்கப்பட்டுள்ளதாக கருதுவோம்.
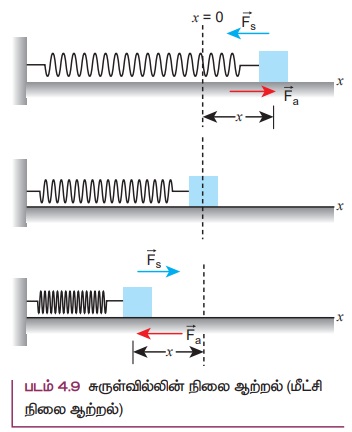
இங்கு x = 0 என்பது சமநிலைப் புள்ளி ஆகும். சுருள்வில்லின் ஒரு முனை ஒரு திடமான சுவரிலும் மறுமுனை நிறையுடனும் இணைக்கப்பட்டுள்ளது.
சுருள்வில்லானது சமநிலையில் இருக்கும் வரை அதன் நிலை ஆற்றல் சுழியாகும். தற்போது ஒரு புறவிசை (![]() a) சுருள்வில் நிறை மீது செயல்படுத்தப்பட்டு விசையின் திசையில் (x) தொலைவு நீட்சியடைகிறது
a) சுருள்வில் நிறை மீது செயல்படுத்தப்பட்டு விசையின் திசையில் (x) தொலைவு நீட்சியடைகிறது
சுருள்வில் விசை (![]() s) என்றழைக்கப்படும் ஒரு மீள்விசை சுருள்வில்லில் உருவாகி நிறையை அதன் தொடக்க நிலைக்குக் கொண்டுவர முயலுகிறது. செயல்படுத்தப்பட்ட விசை மற்றும் சுருள்வில் விசை ஆகியவை எண்மதிப்பில் சமமாகவும் எதிரெதிர் திசையிலும் உள்ளன. அதாவது (
s) என்றழைக்கப்படும் ஒரு மீள்விசை சுருள்வில்லில் உருவாகி நிறையை அதன் தொடக்க நிலைக்குக் கொண்டுவர முயலுகிறது. செயல்படுத்தப்பட்ட விசை மற்றும் சுருள்வில் விசை ஆகியவை எண்மதிப்பில் சமமாகவும் எதிரெதிர் திசையிலும் உள்ளன. அதாவது (![]() a =-
a =-![]() s). ஹுக் விதியின் படி, சுருள்வில்லில் உருவாகும் மீள்விசை,
s). ஹுக் விதியின் படி, சுருள்வில்லில் உருவாகும் மீள்விசை,
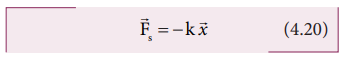
மேற்கண்ட சமன்பாட்டில் உள்ள எதிர்க்குறியானது சுருள்வில்விசை எப்போதும் இடப்பெயர்ச்சி (![]() ) க்கு எதிர்த்திசையில் உள்ளது என்பதைக் குறிக்கிறது மற்றும் k என்பது விசை மாறிலி ஆகும். எனவே செயல்படுத்தப்பட்ட விசை
) க்கு எதிர்த்திசையில் உள்ளது என்பதைக் குறிக்கிறது மற்றும் k என்பது விசை மாறிலி ஆகும். எனவே செயல்படுத்தப்பட்ட விசை ![]() a = + k
a = + k ![]()
நேர்க்குறியானது செயல்படுத்தப்பட்ட விசை இடப்பெயர்ச்சியின் திசையில் உள்ளது என்பதைக் குறிக்கிறது. சுருள்வில் விசை இடப்பெயர்ச்சி ![]() ஐ சார்ந்திருப்பதால் இது மாறும் விசைக்கு ஒரு எடுத்துக்காட்டாகும். சுருள்வில் dx என்ற சிறு தொலைவுக்கு நீட்சியடைவதாகக் கருதுவோம். சுருள்வில்லின் மீது செயல்படுத்தப்பட்ட விசையினால்
ஐ சார்ந்திருப்பதால் இது மாறும் விசைக்கு ஒரு எடுத்துக்காட்டாகும். சுருள்வில் dx என்ற சிறு தொலைவுக்கு நீட்சியடைவதாகக் கருதுவோம். சுருள்வில்லின் மீது செயல்படுத்தப்பட்ட விசையினால் ![]() இடப்பெயர்ச்சி அடைவதற்கு செய்யப்பட்ட வேலை மீட்சி நிலை ஆற்றலாக சேமிக்கப்படுகிறது.
இடப்பெயர்ச்சி அடைவதற்கு செய்யப்பட்ட வேலை மீட்சி நிலை ஆற்றலாக சேமிக்கப்படுகிறது.
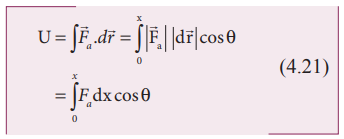
செயல்படுத்தப்பட்ட விசை ![]() மற்றும் இடப்பெயர்ச்சி d
மற்றும் இடப்பெயர்ச்சி d![]() (அதாவது இங்கு dx) ஆகியவை ஒரே திசையில் உள்ளன. தொடக்க நிலையைச் சமநிலை அல்லது நடுநிலையாக எடுத்துக்கொண்டால் x = 0 என்பது தொகையீட்டின் கீழ் எல்லையாக உள்ளது.
(அதாவது இங்கு dx) ஆகியவை ஒரே திசையில் உள்ளன. தொடக்க நிலையைச் சமநிலை அல்லது நடுநிலையாக எடுத்துக்கொண்டால் x = 0 என்பது தொகையீட்டின் கீழ் எல்லையாக உள்ளது.
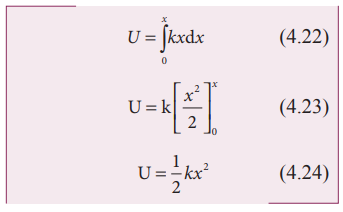
தொடக்கநிலை சுழியில்லை எனில் நிறையானது நிலை xi முதல் xf வரை நகர்த்தப்பட்டால் மீட்சி நிலை ஆற்றல்
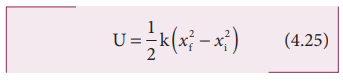
சமன்பாடு (4.24) மற்றும் (4.25) மூலம் அறிவது யாதெனில் நீட்டப்பட்ட சுருள்வில்லின் நிலை ஆற்றலானது விசை மாறிலி k மற்றும் நீட்சி அல்லது அமுக்கம் x ஆகியவற்றைச் சார்ந்தது.
சுருள் வில்லினுள் சேமிக்கப்பட்டுள்ள நிலை ஆற்றலானது சுருள்வில்லுடன் இணைக்கப்பட்டுள்ள நிறையைச் சார்ந்ததல்ல.
சுருள் வில்லின் விசை - இடப்பெயர்ச்சி வரைபடம்
விசையும் இடப்பெயர்ச்சியும் F = - kx என்ற நேர்விகிதத் தொடர்பில் உள்ளதாலும் மற்றும் அவை எதிரெதிர் திசையில் இருப்பதாலும் F மற்றும் x இடையே உள்ள வரைபடமானது படம் 4.10 ல் காட்டியுள்ளவாறு இரண்டு மற்றும் நான்காவது கால்பகுதியில் மட்டுமே அமைந்த நேர் கோடாக உள்ளது. ஒரு F - x வரைபடம் வரைவதன் மூலம் மீட்சி நிலை ஆற்றலை எளிதாகக் கணக்கிடலாம். நிழலிடப்பட்ட பரப்பு (முக்கோணம்) சுருள்வில் விசையால் செய்யப்பட்ட வேலை ஆகும்.
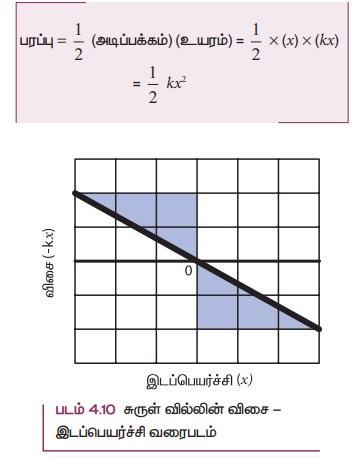
சுருள்வில்லின் நிலை ஆற்றல் - இடப்பெயர்ச்சி வரைபடம்
ஒரு அமுக்கப்பட்ட அல்லது நீட்டப்பட்ட சுருள்வில் தன்னுள் சேமிக்கப்பட்ட நிலை ஆற்றலை அதனுடன் இணைக்கப்பட்ட நிறையின் இயக்க ஆற்றலாக மாற்றுகிறது. நிலை ஆற்றல் - இடப்பெயர்ச்சி வரைபடமானது படம் 4.11 இல் காட்டப்பட்டுள்ளது.
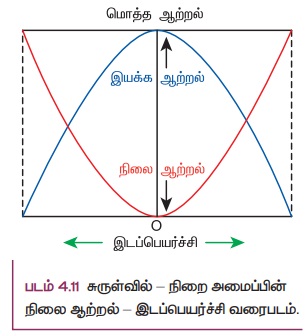
உராய்வற்ற சூழலில், ஆற்றலானது அமைப்பின் மொத்த ஆற்றல் மாறாதவாறு இயக்க ஆற்றலில் இருந்து நிலை ஆற்றலாகவும் மற்றும் நிலை ஆற்றலில் இருந்து இயக்க ஆற்றலாகவும் மீண்டும் மீண்டும் மாற்றமடைகிறது. சமநிலையில்,
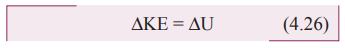
ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகள் (Conservative force and Non Conservative force)
ஆற்றல் மாற்றா விசை (Conservative Force)
ஒரு பொருளை நகர்த்தும் போது விசையினால் அல்லது விசைக்கெதிராக செய்யப்பட்ட வேலை பொருளின் தொடக்க மற்றும் இறுதி நிலைகளை மட்டும் சார்ந்தும், பொருளின் தொடக்க மற்றும் இறுதி நிலைகளுக்கிடையே சென்ற பாதையின் இயல்பைச் சாராமலும் இருப்பின்; அவ்விசை, ஆற்றல் மாற்றா விசை எனப்படும்.
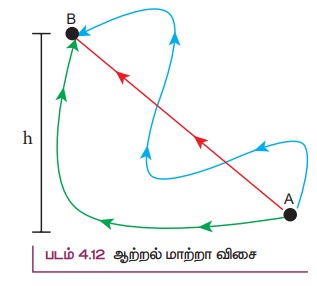
புவியில் A என்ற புள்ளியில் உள்ள ஒரு பொருளைக் கருதுவோம். படம் 412இல் காட்டியுள்ளவாறு இதனை h உயரத்தில் உள்ள B என்ற மற்றொரு புள்ளிக்கு மூன்று பாதைகளில் எடுத்துச் செல்லலாம்.
பாதை எவ்வாறு இருப்பினும் தொடக்க மற்றும் இறுதி நிலைகள் மாறாமல் இருக்கும் வரை புவியீர்ப்பு விசைக்கெதிராக செய்யப்பட்ட வேலை மாறாது. இதுவே புவியீர்ப்பு விசையானது ஆற்றல் மாற்றா விசையாக இருப்பதற்கு காரணமாகும். ஆற்றல் மாற்றா விசை நிலை ஆற்றலின் எதிர்க்குறி சாய்வுக்கு சமமாகும்.
ஒரு பரிமாண நேர்வில்
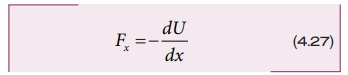
மீட்சி சுருள்வில் விசை, நிலைமின்னியல் விசை, காந்த விசை, புவியீர்ப்பு விசை போன்றவை ஆற்றல் மாற்றா விசைகளுக்கு உதாரணங்கள் ஆகும்.
ஆற்றல் மாற்றும் விசை (Non - Conservative Force)
ஒரு பொருளை விசையினால் அல்லது விசைக்கெதிராக நகர்த்தச் செய்யப்பட்ட வேலை தொடக்க மற்றும் இறுதி நிலைகளுக்கிடையே உள்ள பாதையைச் சார்ந்திருப்பின் அவ்விசை ஆற்றல் மாற்றும் விசை எனப்படும். இதன் பொருள் வேவ்வேறு பாதைகளில் செய்யப்பட்ட வேலையின் மதிப்பு மாறுபடும் என்பதாகும்.
1. உராய்வு விசைகள் ஆற்றல் மாற்றும் விசைகள் ஆகும். ஏனென்றால் உராய்வுக்கு எதிராக செய்யப்பட்ட வேலை பொருள் நகர்ந்த பாதையின் தொலைவைச் சார்ந்தது.
2. காற்றுத்தடையால் ஏற்படும் விசை, பாகியல் விசை ஆகியவையும் ஆற்றல் மாற்றும் விசைகள் ஆகும். இவ்விசையால் அல்லது விசைக்கெதிராக செய்யப்பட்ட வேலை இயக்கத்தின் திசைவேகத்தைச் சார்ந்தது.
ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகளின் பண்புகள் அட்டவணை 4.3இல் தொகுக்கப்பட்டுள்ளன.

ஆற்றல் மாறா விதி (Law of Conservation of energy)
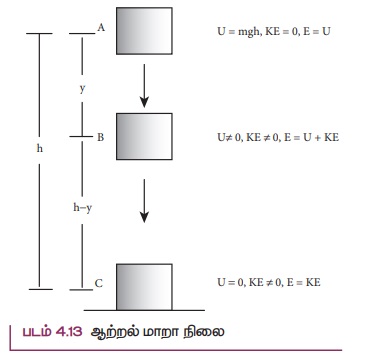
ஒரு பொருளை நாம் மேல்நோக்கி எறிந்தால் அதன் இயக்க ஆற்றல் குறைந்து கொண்டே செல்கிறது மற்றும் அதன் நிலை ஆற்றல் அதிகரித்துக் கொண்டே செல்கிறது (காற்றுத் தடையை புறக்கணிக்கும்போது). பொருளானது பெரும உயரத்தை அடையும்போது ஆற்றல் முழுவதும் நிலை ஆற்றலாகும். அதுபோன்று பொருளானது பெரும் உயரத்தில் இருந்து விழுந்தால் அதன் இயக்க ஆற்றல் அதிகரிக்கும் மற்றும் நிலை ஆற்றல் குறையும். தரையைத் தொடும்போது அதன் ஆற்றல் முழுவதும் இயக்க ஆற்றலாகும். படம் 4.13 இல் காட்டியுள்ளவாறு இடைப்பட்ட புள்ளிகளில் ஆற்றலானது இயக்க ஆற்றலாகவும் நிலை ஆற்றலாகவும் இருக்கும். பொருளானது தரையை அடையும் போது இயக்க ஆற்றல் முழுவதுமாக ஒலி, வெப்பம், ஒளி மற்றும் பொருளின் உருக்குலைவு போன்ற வேறுவகை ஆற்றலாக வெளிப்படும்.
இந்த உதாரணத்தில் ஒவ்வொரு புள்ளியிலும் நிலையாற்றல் மற்றும் இயக்க ஆற்றல் மாறும். எனினும், இயக்க ஆற்றல் மற்றும் நிலை ஆற்றலின் கூடுதல் அதாவது மொத்த இயந்திர ஆற்றல் எப்போதும் மாறாது. இது மொத்த ஆற்றல் மாறாது என்பதைக் குறிக்கிறது. இதுவே ஆற்றல் மாறா விதியாகும்.
ஆற்றல் மாறா விதியின்படி ஆற்றலை ஆக்கவோ அழிக்கவோ இயலாது. ஆற்றலானது ஒரு வகையிலிருந்து மற்றொரு வகையாக மாறக்கூடியது. ஆனால் ஒரு தனித்த அமைப்பின் மொத்த ஆற்றல் மாறிலியாக இருக்கும்.
படம் 4.13 விளக்குவது யாதெனில், h உயரத்தில் ஓய்வில் உள்ள ஒரு பொருளின் மொத்த ஆற்றல் முழுவதும் நிலை ஆற்றல் (U=mgh) மட்டுமே. மேலும் h உயரத்தில் அதன் இயக்க ஆற்றல் (KE) சுழியாகும். பொருள் கீழே விழும்போது ‘y’ தொலைவில் அதன் நிலையாற்றல் மற்றும் இயக்க ஆற்றல் சுழியாகாது. அதேசமயம் h உயரத்தில் இருந்த அதே அளவில் மொத்த ஆற்றல் மாறாமல் இருக்கும். பொருள் தரையைத் தொட நெருங்கும் போது நிலை ஆற்றல் சுழியாகும் மற்றும் மொத்த ஆற்றல் இயக்க ஆற்றலாக மட்டுமே இருக்கும்.
செங்குத்து வட்ட இயக்கம் [Motion in a vertical circle]
m நிறையுள்ள ஒரு பொருள் நிறையற்ற, நீட்சித் தன்மையற்ற நூலின் ஒரு முனையில் இணைக்கப்படுகிறது. மேலும், நூலின் மறுமுனையானது நிலையாக இருக்குமாறு பொருத்தப்பட்டுள்ளது. அந்தப்பொருள் செங்குத்துத் தளத்தில் அமைந்த வட்ட இயக்கத்தை மேற்கொள்வதாகக் கருதுவோம். நூலின் நீளமானது வட்டப்பாதையின் ஆரமாக (![]() ) உள்ளது. (படம் 4.14) படத்தில் காட்டியுள்ளவாறு பொருளின் இயக்கத்தைப் பற்றி அறிய தனித்த பொருளின் விசைப்படம் (Free body diagram) ஒன்றைக் கருதுவோம். இங்கு நிலை வெக்டர் (
) உள்ளது. (படம் 4.14) படத்தில் காட்டியுள்ளவாறு பொருளின் இயக்கத்தைப் பற்றி அறிய தனித்த பொருளின் விசைப்படம் (Free body diagram) ஒன்றைக் கருதுவோம். இங்கு நிலை வெக்டர் (![]() ) ஆனது செங்குத்தான கீழ்நோக்கிய திசையுடன் θ கோணத்தை ஏற்படுத்தி படத்தில் உள்ளவாறு உடனடி திசைவேகத்தைக் கொண்டுள்ளது.
) ஆனது செங்குத்தான கீழ்நோக்கிய திசையுடன் θ கோணத்தை ஏற்படுத்தி படத்தில் உள்ளவாறு உடனடி திசைவேகத்தைக் கொண்டுள்ளது.
பொருளின் மீது இரு விசைகள் செயல்படுகின்றன.
1. கீழ் நோக்கி செயல்படும் புவியீர்ப்பு விசை
2. நூலின் வழியே செயல்படும் இழுவிசை
பொருளின் மீது நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்த, தொடுகோட்டுத் திசையில்,
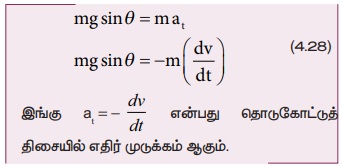
ஆரத்திசையில்,

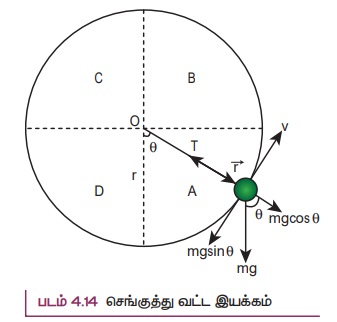
இயக்கத்தை நன்கு புரிந்து கொள்ளும் வகையில் வட்டத்தை A, B, C, D என்ற நான்கு பகுதிகளாகப் பிரிக்கலாம். மேற்கண்ட இரு சமன்பாடுகளில் இருந்து கீழ்க்கண்டவாறு நான்கு முக்கிய கருத்துகளைப் புரிந்து கொள்ளலாம்.
(i) பொருளானது அனைத்து θ மதிப்புக்களுக்கும் (θ = 0° தவிர) தொடுகோட்டுத் திசையில் முடுக்கத்தை (g sin θ) கொண்டிருக்கிறது. இந்த செங்குத்து வட்ட இயக்கம் ஒரு சீரான வட்ட இயக்கம் அல்ல என்பது தெளிவாகிறது.
(ii) சமன்பாடுகள் (4.28) மற்றும் (4.29) இல் இருந்து அறிந்து கொள்வது என்னவெனில் இயக்கத்தின் போது திசைவேகத்தின் எண் மதிப்பு மாறுவதால், நூலின் இழுவிசையும் மாறுகின்றது.
(iii) சமன்பாடு (4.29), T = mg cos θ + mv2/r சுட்டிக்காட்டுவது வட்டத்தின் A மற்றும் D பகுதிகளில் (–π/2 < θ < π/2 மற்றும் cos θ நேர்க்குறி) mg cos θ எப்போதும் சுழியைவிட அதிகமாகும். எனவே திசைவேகம் சுழியானாலும் இழுவிசை சுழியாகாது.
(iv) சமன்பாடு (4.29), mv2/r = T - mg cosθ மேலும் சுட்டிக்காட்டுவது வட்டத்தின் B மற்றும் C பகுதிகளில் (–π/2 < θ < 3π/2 மற்றும் cosθ எதிர்க்குறி), சமன்பாட்டின் இரண்டாவது பகுதி (- mg cos θ) எப்போதும் சுழியை விட அதிகமாகும். எனவே இழுவிசை சுழியானாலும் திசைவேகம் சுழியாகாது.
செங்குத்து வட்ட இயக்கம் தொடர்பான கணக்குகளை தீர்வுகாணும்போது மேற்கண்ட கருத்துக்களை மனதில் கொள்ள வேண்டும்.
படம் 4.15 இல் காட்டியுள்ளவாறு அடிப்பக்கப் புள்ளி 1 மற்றும் மேற்பக்கப் புள்ளி 2 ஆகிய இரு நிலைகளை மட்டும் கருத்தில் கொண்டு மேலும் பகுப்பாய்வு செய்வோம். பொருளின் திசைவேகமானது அடிப்பக்கப்புள்ளி 1 இல் ![]() எனவும், மேற்பக்கப் புள்ளி 2 இல்
எனவும், மேற்பக்கப் புள்ளி 2 இல்![]() எனவும் வேறு எந்த புள்ளியிலும்
எனவும் வேறு எந்த புள்ளியிலும் ![]() எனவும் கொள்க. திசைவேகத்தின் திசை அனைத்துப் புள்ளிகளிலும் வட்டப்பாதையின் தொடுகோட்டுத் திசையில் உள்ளது. அடிப்பக்கப் புள்ளியிலிருந்து நூலின் இழுவிசையானது
எனவும் கொள்க. திசைவேகத்தின் திசை அனைத்துப் புள்ளிகளிலும் வட்டப்பாதையின் தொடுகோட்டுத் திசையில் உள்ளது. அடிப்பக்கப் புள்ளியிலிருந்து நூலின் இழுவிசையானது ![]() எனவும், மேற்பக்கப் புள்ளியிலிருந்து இழுவிசை
எனவும், மேற்பக்கப் புள்ளியிலிருந்து இழுவிசை ![]() எனவும் வேறு எந்த புள்ளியிலும் இழுவிசை
எனவும் வேறு எந்த புள்ளியிலும் இழுவிசை ![]() எனவும் கொள்க. ஒவ்வொரு புள்ளியிலும் இழுவிசை மையப்புள்ளியை நோக்கி செயல்படுகிறது. ஆற்றல் மாறா விதியைப் பயன்படுத்தி இந்த இரு புள்ளிகளிலும் இழுவிசைகள் மற்றும் திசைவேகங்களைக் கணக்கிடலாம்.
எனவும் கொள்க. ஒவ்வொரு புள்ளியிலும் இழுவிசை மையப்புள்ளியை நோக்கி செயல்படுகிறது. ஆற்றல் மாறா விதியைப் பயன்படுத்தி இந்த இரு புள்ளிகளிலும் இழுவிசைகள் மற்றும் திசைவேகங்களைக் கணக்கிடலாம்.
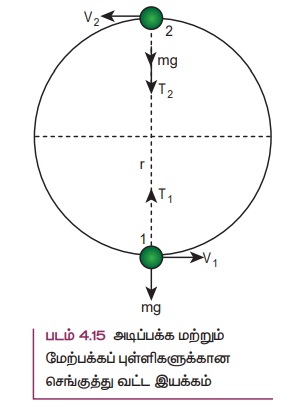
அடிப்பக்கப் புள்ளி (1):
பொருளானது அடிப்பக்கப் புள்ளி 1 இல் உள்ள போது புவியீர்ப்பு விசை m ![]() பொருளின் மீது செங்குத்தாக கீழ்நோக்கி செயல்படுகிறது மற்றும் இழுவிசை
பொருளின் மீது செங்குத்தாக கீழ்நோக்கி செயல்படுகிறது மற்றும் இழுவிசை ![]() 1 செங்குத்தாக மேல்நோக்கி அதாவது மையப்புள்ளியை நோக்கிச் செயல்படுகிறது. சமன்பாடு (4.29) இல் இருந்து நாம் பெறுவது
1 செங்குத்தாக மேல்நோக்கி அதாவது மையப்புள்ளியை நோக்கிச் செயல்படுகிறது. சமன்பாடு (4.29) இல் இருந்து நாம் பெறுவது
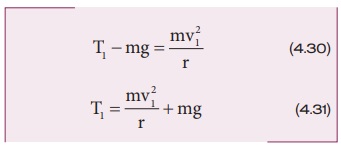
மேற்பக்கப் புள்ளி (2):
மேற்பக்கப் புள்ளி 2 இல் பொருளின் மீதான புவியீர்ப்பு விசை m![]() மற்றும் இழுவிசை
மற்றும் இழுவிசை ![]() 2 ஆகிய இரண்டும் கீழ்நோக்கி அதாவது மையப்புள்ளியை நோக்கி செயல்படுகிறது.
2 ஆகிய இரண்டும் கீழ்நோக்கி அதாவது மையப்புள்ளியை நோக்கி செயல்படுகிறது.
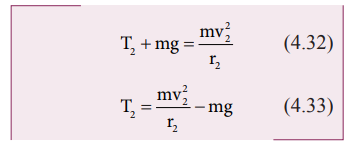
சமன்பாடுகள் (4.31) மற்றும் (4.33) இல் இருந்து T1 > T2 என அறியலாம். இழுவிசையின் வேறுபாடு T1 – T2 ஆனது சமன்பாடு (4.33)ஐ சமன்பாடு (4.31) இல் இருந்து கழிப்பதன் மூலம் பெறப்படுகிறது.
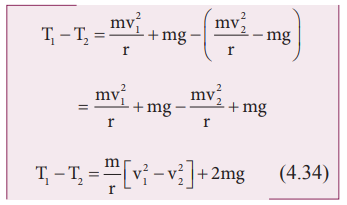
புள்ளி 1 மற்றும் 2 இல் ஆற்றல் மாறா விதியைப் பயன்படுத்தி [v12 – v22] மதிப்பை எளிதாகக் கணக்கிடலாம்.
இழுவிசையும் பொருள் செல்லும் திசையும் எப்போதும் ஒன்றுக்கொன்று செங்குத்தாக உள்ளதால் இழுவிசையானது பொருளின்மீது எவ்வித வேலையும் செய்யாது.
புவியீர்ப்பு விசையானது பொருளின் மீது வேலை செய்கிறது. மேலும் அது ஆற்றல் மாற்றா விசை என்பதால் இயக்கம் முழுவதும் பொருளின் மொத்த ஆற்றல் மாறாது.

புள்ளி 1 இல் நிலை ஆற்றல் U1 = 0 (புள்ளி 1 ஐ குறிப்புப் புள்ளியாக எடுத்துக்கொள்வதன் மூலம்) புள்ளி 1 இல் இயக்க ஆற்றல் 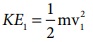
புள்ளி 1 இல் மொத்த ஆற்றல்
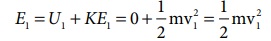
இதுபோன்றே புள்ளி 2 இல் நிலை ஆற்றல் U2 = mg (2r)
(புள்ளி 1 இல் இருந்து h மதிப்பு 2r ஆகும்)
புள்ளி 2 இல் இயக்க ஆற்றல் 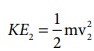
புள்ளி 2 இல் மொத்த ஆற்றல்
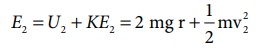
சமன்பாடு (4.35) இல் உள்ளவாறு ஆற்றல் மாறா விதிப்படி
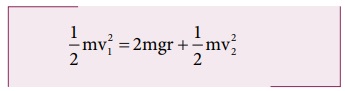
மாற்றியமைக்க
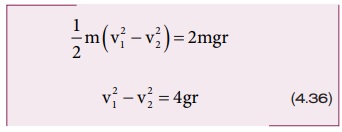
சமன்பாடு (4.34) இல் சமன்பாடு (4.36) ஐ பிரதியிட
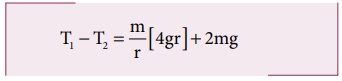
எனவே இழுவிசையில் மாறுபாடானது
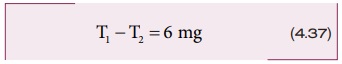
மேற்பக்கப் புள்ளி (2) இல் சிறும் வேகம்:
பொருளானது புள்ளி 2 இல் ஒரு சிறும் வேகத்தைக் கொண்டிருக்க வேண்டும், இல்லையெனில் புள்ளி 2 ஐ அடையும் முன்பாக நூலானது தளர்வுற்று அதனால் பொருள் வட்டப்பாதையை நிறைவு செய்யாது. இந்த சிறும் வேகத்தைக் கணக்கிட சமன்பாடு (4.33) இல் இழுவிசை T2 = 0 எனக் கொள்வோம்.
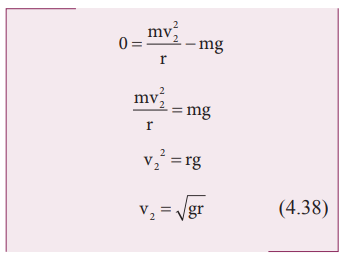
பொருளானது வட்டப்பாதையில் தொடர்ந்து இயங்க புள்ளி 2 இல் v2 ≥ √gr என்ற வேகத்தைக் கொண்டிருக்க வேண்டும்.
அடிப்புள்ளி (1) இல் சிறும் வேகம்:
புள்ளி 2 இல் இந்த சிறும வேகத்தைப் (v2=√gr) பெற பொருளானது புள்ளி 1லும் ஒரு சிறும் வேகத்தைக் கொண்டிருக்க வேண்டும்.
சமன்பாடு (4.36) ஐப் பயன்படுத்தி புள்ளி 1 இல் சிறும் வேகத்தை நாம் காணலாம்.
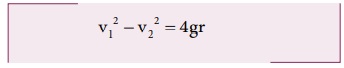
சமன்பாடு (4.38) ஐ (4.36) இல் பிரதியிட
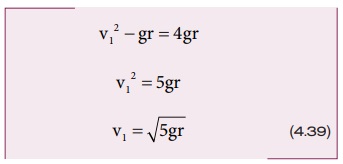
பொருளானது வட்டப்பாதையில் தொடர்ந்து இயங்க புள்ளி 1 இல் (v1≥√5gr) என்ற வேகத்தைக் கொண்டிருக்க வேண்டும்.
சமன்பாடுகள் (4.38) மற்றும் (4.39) இல் இருந்து அறிவது என்னவெனில் பொருள் வட்டப்பாதையை விட்டு விலகாமல் நிறைவு செய்ய அடிப்புள்ளி 1 இல் சிறும் வேகமானது மேற்பக்கப் புள்ளி 2 இல் உள்ள சிறும் வேகத்தை விட √5 மடங்கு இருக்க வேண்டும்.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் இயக்க ஆற்றல்
எடுத்துக்காட்டு 4.7
2 kg மற்றும் 4 kg நிறை கொண்ட இரு பொருள்கள் 20 kg ms-1 என்ற சம உந்தத்துடன் இயங்குகின்றன.
(a) அவை சம இயக்க ஆற்றலைப் பெற்றிருக்குமா?
(b) அவை சம வேகத்தைப் பெற்றிருக்குமா?
தீர்வு
(a) பொருளின் இயக்க ஆற்றல்

KE1 ≠ KE2 என அறியவும். அதாவது இருபொருட்களும் சம உந்தத்தைப் பெற்றிருந்தாலும் அவற்றின் இயக்க ஆற்றல் சமமல்ல. கனமான பொருள் இலேசான பொருளை விட குறைவான இயக்க ஆற்றலைப் பெற்றுள்ளது. ஏனென்றால் கொடுக்கப்பட்ட உந்தத்திற்கு இயக்க ஆற்றலானது நிறைக்கு எதிர் விகிதத்தில் உள்ளது.
KE ∝ 1/m
(b) உந்தம் p = mv என்பதால் இரு பொருட்களும் சம வேகத்தைப் பெற்றிருக்காது.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் நிலை ஆற்றல்
எடுத்துக்காட்டு 4.8
2 kg நிறையுள்ள பொருள் தரையிலிருந்து 5 m உயரத்திற்குக் கொண்டு செல்லப்படுகிறது (g = 10 m s-2) எனில்
a) பொருளினுள் சேமிக்கப்பட்டுள்ள நிலையாற்றல் யாது?
b) இந்த நிலையாற்றல் எங்கிருந்து கிடைத்தது?
c) பொருளை அந்த உயரத்திற்கு எடுத்துச் செல்ல எவ்வளவு புறவிசை செயல்பட வேண்டும்?
d) பொருளானது 'h' உயரத்திற்கு எடுத்துச் செல்லப்படும் போது அதன் மீது செயல்படும் நிகர விசை யாது?
தீர்வு:
a) நிலையாற்றல் U=m g h = 2 × 10 × 5 = 100 J இங்கு நேர்க்குறியானது பொருளினுள் ஆற்றல் சேமிக்கப்பட்டுள்ளதைக் குறிக்கிறது.
b) இந்த நிலையாற்றலானது, புற விசையை செயல்படுத்தும் வெளிப்புற அமைப்பிலிருந்து பொருளுக்கு மாற்றப்பட்டுள்ளது.
c) பொருளை 5 m உயரத்திற்கு எடுத்துச் செல்ல செயல்படுத்தப்பட்ட புற விசை ![]() ஆனது
ஆனது 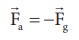
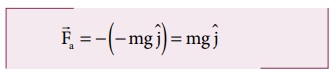
![]() ஆனது செங்குத்தாக மேல்நோக்கிய திசையில் செயல்படும் ஓரலகு வெக்டர் ஆகும்.
ஆனது செங்குத்தாக மேல்நோக்கிய திசையில் செயல்படும் ஓரலகு வெக்டர் ஆகும்.
d) நிலையாற்றலின் வரையறையில் இருந்து, பொருளானது மாறாத் திசைவேகத்தில் நகர்த்தப்பட வேண்டும். எனவே, பொருளின் மீது செயல்படும் நிகர விசை சுழி ஆகும்.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் மீட்சி நிலை ஆற்றல்
எடுத்துக்காட்டு 4.9
இரு சுருள்வில்கள் A மற்றும் B யின் சுருள்மாறிலிகள் kA > kB என்றவாறு உள்ளன. அவை சம விசைகளால் நீட்சியடையச் செய்யப்பட்டால் எந்த சுருள்வில்லின் மீது அதிக வேலை செய்யப்பட வேண்டும்?
தீர்வு
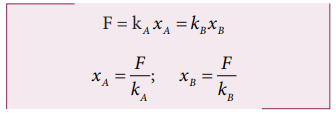
சுருள்வில்கள் மீது செய்யப்பட்ட வேலை சுருள்வில்களில் நிலை ஆற்றலாக சேமிக்கப்படுகிறது.

kA > kB, குறிப்பது UB > UA ஆகும். எனவே A - வை விட B - இன் மீது அதிக வேலை செய்யப்பட வேண்டும்.
எடுத்துக்காட்டு 4.10
m நிறையுள்ள ஒரு பொருள் சுருள்வில்லுடன் இணைக்கப்பட்டு, செயல்படுத்தப்படும் விசையினால் அது நடுநிலையில் இருந்து 25 cm அளவிற்கு நீட்சியடைகிறது.
(a) சுருள்வில் - நிறை அமைப்பில் சேமிக்கப்பட்ட நிலை ஆற்றலைக் கணக்கிடுக.
(b) இந்த நீட்சியில் சுருள்வில் விசையால் செய்யப்பட்ட வேலை யாது?
(c) சுருள்வில்லானது அதே 25 cm அளவிற்கு அமுக்கப்பட்டால் சேமிக்கப்படும் நிலை ஆற்றல் மற்றும் அமுக்கத்தின் போது சுருள்வில் விசையால் செய்யப்பட்ட வேலை ஆகியவற்றைக் கணக்கிடுக. (சுருள்வில் மாறிலி k = 0.1 N m-1)
தீர்வு
சுருள்வில் மாறிலி k = 0.1 Nm-1
இடப்பெயர்ச்சி x = 25 cm = 0.25 m
(a) சுருள்வில்லில் சேமிக்கப்பட்ட நிலை ஆற்றல்
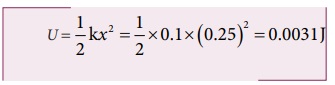
(b) சுருள்வில் விசை ![]() ஆல் செய்யப்பட்ட வேலை Ws மதிப்பு
ஆல் செய்யப்பட்ட வேலை Ws மதிப்பு
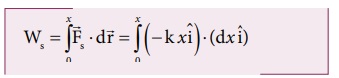
சுருள்வில்விசை ![]() எதிர்க்குறி x அச்சின் திசையில் செயல்படுகிறது. அதேசமயம் நீட்சியானது நேர்க்குறி x அச்சின் திசையில் செயல்படுகிறது.
எதிர்க்குறி x அச்சின் திசையில் செயல்படுகிறது. அதேசமயம் நீட்சியானது நேர்க்குறி x அச்சின் திசையில் செயல்படுகிறது.
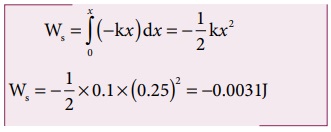
வெளிப்புற அமைப்பால் செய்யப்பட்ட வேலையின் மூலம் நிலை ஆற்றலை வரையறுக்கலாம். நிலை ஆற்றலில் உள்ள நேர்க்குறி, ஆற்றலானது அமைப்பிலிருந்து பொருளுக்கு மாற்றப்படுவதைக் குறிக்கிறது. ஆனால் இந்நேர்வில் மீள் விசையால் செய்யப்பட்ட வேலை எதிர்க்குறி மதிப்புடையது. ஏனென்றால் மீள்விசையானது இடப்பெயர்ச்சியின் திசைக்கு எதிர்த்திசையில் செயல்படுகிறது.
(c) அமுக்கத்தின் போதும் பொருளில் அதே அளவு நிலை ஆற்றல் சேமிக்கப்படுகிறது.
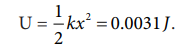
அமுக்கப்படும் போது சுருள்வில் மீள் விசையால் செய்யப்பட்ட வேலை
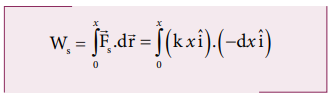
அமுக்கப்படும் நேர்வில் சுருள்வில் மீள்விசை நேர்க்குறி x அச்சை நோக்கி செயல்படுகிறது. மற்றும் இடப்பெயர்ச்சியானது எதிர்க்குறி x அச்சின் திசையில் உள்ளது.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகள்
எடுத்துக்காட்டு 4.11
கீழ்கண்ட நேர்வுகளில் புவியீர்ப்பு விசையினால் செய்யப்பட்ட வேலையைக் கணக்கிடுக.
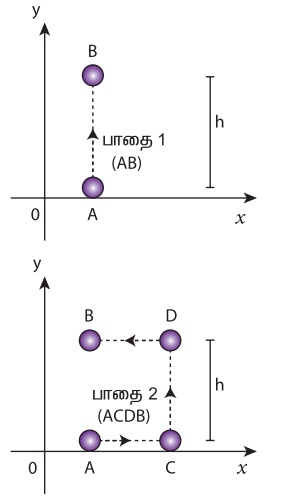
தீர்வு
விசை 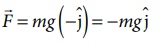
இடப்பெயர்ச்சி வெக்டர் 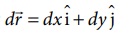
(இடப்பெயர்ச்சி இரு பரிமாணத்தில் உள்ளதால் அலகு வெக்டர்கள் ![]() மற்றும்
மற்றும் ![]() பயன்படுத்தப்படுகிறது)
பயன்படுத்தப்படுகிறது)
(a) இயக்கமானது செங்குத்தாக மட்டும் உள்ளதால், இடப்பெயர்ச்சியின் கிடைத்தளக்கூறு dx சுழியாகும். எனவே பாதை 1 இன் வழியே விசையினால் செய்யப்பட்ட வேலை (h தொலைவிற்கு)
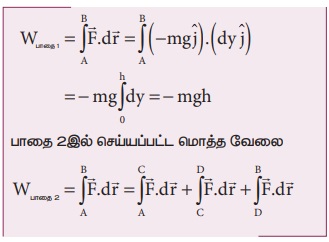
ஆனால்
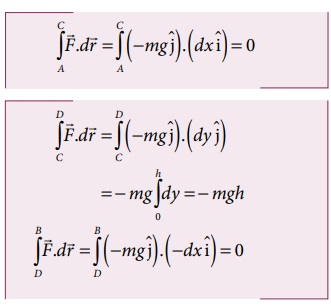
எனவே பாதை 2 இன் வழியே விசையினால் செய்யப்பட்ட மொத்த வேலை
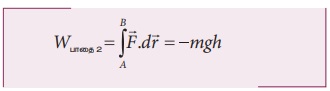
ஆற்றல் மாற்றா விசையினால் செய்யப்பட்ட வேலை பாதையைச் சார்ந்ததல்ல என்பதை அறியவும்.
எடுத்துக்காட்டு 4.12
2 kg நிறையுள்ள ஒரு பொருள் இயக்க உராய்வுக் குணகம் 0.9 கொண்டுள்ள ஒரு பரப்பில் 20 N புறவிசையினால் 10 m தொலைவிற்கு நகர்த்தப்படுவதாகக் கருதுக. புறவிசை மற்றும் இயக்க உராய்வினால் செய்யப்பட்ட வேலை என்ன? முடிவைப் பற்றிய கருத்தைக் கூறுக (g = 10 ms-2 எனக் கொள்க)
தீர்வு
m = 2 kg, d = 10 m, Fext = 20 N, µk = 0.9
ஒரு பொருள் கிடைமட்டப் பரப்பில் இயங்கும்போது அது இரு விசைகளைப் பெறுகிறது.
(a) புற விசை Fext = 20 N
(b) இயக்க உராய்வு விசை
fk = μk mg = 0.9 × (2) × 10 = 18N.
புறவிசையினால் செய்யப்பட்ட வேலை
Wext = Fd = 20 × 10 = 200 J
இயக்க உராய்வு விசையினால் செய்யப்பட்ட வேலை
Wk = fkd = (-18) × 10 = -180 J
இங்கு எதிர்க்குறியானது இயக்க உராய்வு விசை, இடப்பெயர்ச்சியின் திசைக்கு எதிராக உள்ளதைக் குறிக்கிறது.
பொருளின் மீது செய்யப்பட்ட மொத்த வேலை
Wtotal = Wext + Wk = 200 - 180 = 20 J
உராய்வு விசை ஒரு ஆற்றல் மாற்றும் விசை என்பதால் புறவிசையால் கொடுக்கப்பட்ட 200 J இல் 180 J இழக்கப்பட்டது மற்றும் இதனை மீட்டெடுக்க இயலாது.
எடுத்துக்காட்டு 4.13
1 kg நிறையுள்ள ஒரு பொருள் h = 10 m உயரத்திலிருந்து விழுகிறது.
(a) h = 10 m உயரத்தில் பொருளின் மொத்த ஆற்றல்
(b) h = 4 m உயரத்தில் பொருளின் நிலை ஆற்றல்
(c) h = 4 m உயரத்தில் பொருளின் இயக்க ஆற்றல்
(d) பொருள் தரையில் மோதும் வேகம் ஆகியவற்றைக் கணக்கிடுக.
(g = 10 ms-2 எனக் கொள்க)
தீர்வு
(a) புவியீர்ப்பு விசை ஆற்றல் மாற்றா விசையாகும். எனவே இயக்கம் முழுவதும் மொத்த ஆற்றல் மாறாமல் இருக்கும்.
h = 10 m உயரத்தில் மொத்த ஆற்றல் (E) முழுவதும் நிலை ஆற்றலாக இருக்கும்.
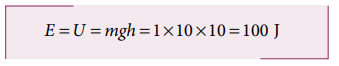
(b) h = 4 m உயரத்தில் நிலை ஆற்றல்
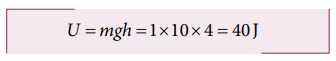
(c) இயக்கம் முழுவதும் மொத்த ஆற்றல் மாறிலி என்பதால் h = 4 m உயரத்தில் இயக்க ஆற்றலானது
KE = E - U = 100 - 40 = 60J
மாறாக 4 m உயரத்தில் பொருளின் திசைவேகத்தில் இருந்தும் இயக்க ஆற்றலைக் காணலாம். 6 m வீழ்ந்த பிறகு உள்ள திசைவேகத்தை இயக்கச் சமன்பாட்டிலிருந்து கணக்கிடலாம்.
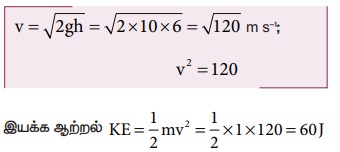
(d) பொருள் தரையில் மோதும் நிலையில் மொத்த ஆற்றல் முழுவதும் இயக்க ஆற்றலாகும். மேலும் நிலை ஆற்றல் U = 0
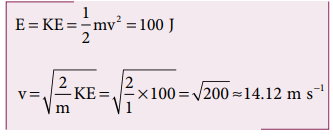
எடுத்துக்காட்டு 4.14
படத்தில் காட்டியுள்ளவாறு 100 kg நிறையுள்ள ஒரு பொருள் தரையிலிருந்து 10 m உயரத்திற்கு இரு மாறுபட்ட வழிகளில் தூக்கப்படுகிறது. இரு நேர்வுகளிலும் புவியீர்ப்பால் செய்யப்பட்ட வேலை என்ன? சாய்தளத்தின் வழியாக பொருளை எடுத்துச் செல்வது எளிதாக உள்ளது ஏன்?
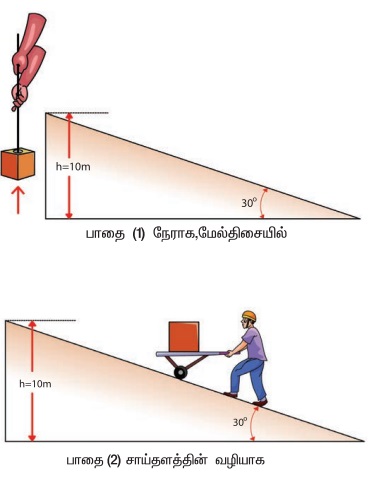
தீர்வு
m = 100 kg, h = 10 m
பாதை (1) இன் வழியே:
பொருளை 10 m உயரத்திற்குத் தூக்கத் தேவையான சிறும் விசை F1 ஆனது புவியீர்ப்பு விசைக்குச் சமமாக இருக்க வேண்டும்.
F1 = mg = 100 × 10 = 1000 N
பாதை (1) இன் வழியே நகர்ந்த தொலைவு h = 10 m
பாதை (1) இன் வழியே பொருளின் மீது செய்யப்பட்ட வேலை
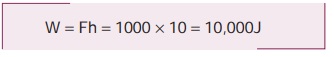
பாதை (2) இன் வழியே:
சாய்தளத்தின் வழியே பொருளைக் கொண்டு செல்ல பொருளின் மீது நாம் செலுத்தும் சிறும விசை F2 ஆனது mg-க்கு சமமாக இல்லை, மாறாக mg sin θ -க்கு சமமாகும். இங்கு θ = 30°
mg sin θ = 100 × 10 × sin30°
= 100 × 10 × 0.5 = 500 N
எனவே (mg sin θ < mg)
சாய்தளப் பாதையின் நீளமானது
l = h/sin30° = 10/0.5 = 20m
பாதை (2) இன் வழியே பொருளின் மீது செய்யப்பட்ட
வேலை W = F2 l = 500 × 20 = 10,000 J
புவியீர்ப்பு விசையானது ஆற்றல் மாற்றா விசை என்பதால் புவியீர்ப்பால் பொருளின் மீது செய்யப்பட்ட வேலை அதனை கொண்டு சென்ற பாதையைச் சார்ந்ததல்ல.
இரு பாதைகளிலும் புவியீர்ப்பு விசையால் செய்யப்பட்ட வேலை 10,000 J ஆகும்.
பாதை (1) இன் வழியே:
குறைவான தொலைவு நகர்த்த புவியீர்ப்புக்கு எதிராக அதிகமான விசை செலுத்த வேண்டியுள்ளது.
பாதை (2) இன் வழியே:
அதிகமான தொலைவு நகர்த்த புவியீர்ப்புக்கு எதிராக குறைவான விசை செலுத்த வேண்டியுள்ளது.
சாய்தளத்தின் வழியே செலுத்தப்பட வேண்டிய விசை குறைவாக உள்ளதால் சாய்தளத்தின் வழியாக பொருளை எடுத்துச் செல்வது எளிதாக உள்ளது.
எடுத்துக்காட்டு 4.15
m நிறையுள்ள ஒரு பொருள் தரையிலிருந்து V0 என்ற தொடக்க வேகத்துடன் எறியப்படுகிறது. h உயரத்தில் அதன் வேகத்தைக் காண்க.
தீர்வு
புவியீர்ப்பு விசை ஆற்றல் மாற்றா விசை என்பதால் இயக்கம் முழுவதும் மொத்த ஆற்றல் மாறாது.
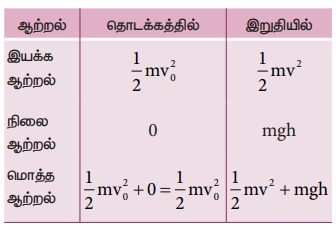
h உயரத்தில் நிலை ஆற்றல், இயக்க ஆற்றல் மற்றும் மொத்த ஆற்றல் ஆகியவற்றின் இறுதி மதிப்புகள் கணக்கிடப்பட்டுள்ளன.
ஆற்றல் மாறா விதியின் படி தொடக்க மற்றும் இறுதி மொத்த ஆற்றல்கள் சமமாகும்.
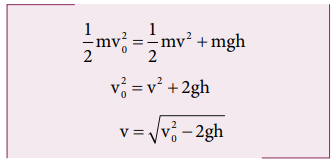
பாடப்பகுதி (2.11.2) இல் இயக்கவியல் சமன்பாட்டைப் பயன்படுத்தி நுண்கணித முறைப்படி இது போன்ற முடிவு பெறப்பட்டதை கவனிக்கவும். எனினும் ஆற்றல் மாறா விதியின் முறைப்படி கணக்கிடுவது நுண்கணித முறையைவிட மிகவும் எளிதாக உள்ளது.
எடுத்துக்காட்டு 4.16
ஒரு சுருள்வில்லுடன் இணைக்கப்பட்ட 2 kg நிறையுள்ள ஒரு பொருள் அதன் சமநிலையிலிருந்து x = 10 m என்ற தொலைவுக்கு நகர்த்தப்படுகிறது. சுருள்வில் மாறிலி k = 1 N m-1 மற்றும் பரப்பு உராய்வற்றதாகக் கருதுக.
(a) பொருளானது சமநிலையைக் கடக்கும்போது அதன் வேகம் என்ன?
(b) பொருளானது சமநிலையைக் கடக்கும் போதும், x = ± 10 m என்ற விளிம்பு நிலையை கடக்கும்போதும் பொருளின் மீது செயல்படும் விசை யாது?
தீர்வு
(a) சுருள்வில் விசை ஒரு ஆற்றல் மாற்றா விசை ஆகையால் மொத்த ஆற்றல் மாறிலி ஆகும். x = 10 m எனும்போது மொத்த ஆற்றல் ழுமுவதும் நிலை ஆற்றலாக மட்டுமே இருக்கும்.
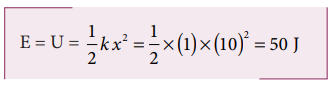
பொருள் சமநிலையைக் கடக்கும்போது (x = 0) நிலை ஆற்றலானது
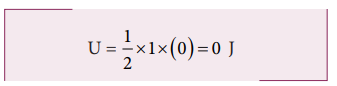
இந்நிலையில் முழு ஆற்றலும் இயக்க ஆற்றலாக மட்டுமே உள்ளது.
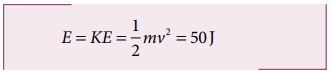
வேகம்
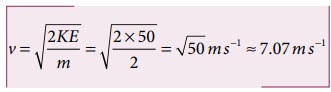
(b) சுருள்வில்லின் மீள்விசை F = – kx என்பதால் பொருளானது நடுநிலையைக் கடக்கும் போது அது எவ்விசையையும் உணராது. நடுநிலையில் பொருளானது மிக வேகமாக நகருகிறது என்பதை அறியவும். பொருளானது x = +10 m (நீட்சி) என்ற நிலையில் உள்ள போது விசை F = - k x
F = - (1) (10) = - 10 N இங்கு எதிர்க்குறியானது விசை நடுநிலையை நோக்கி, அதாவது எதிர் x அச்சை நோக்கி உள்ளதைக் குறிக்கிறது. மேலும் பொருளானது
x = -10 m (அமுக்கம்) என்ற நிலையில் உள்ளபோது அது உணரும் விசை
F = - (1) (-10) = + 10 N. இங்கு நேர்க்குறியானது விசை நேர் x - அச்சை நோக்கி உள்ளதைக் குறிக்கிறது.
x = ±10 m என்ற நிலையில் பொருளானது இந்த இரு விளிம்பு புள்ளிகளிலும் பெரும் விசையை உணர்ந்தாலும் கணநேர ஓய்வு நிலைக்கு வருகிறது.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் செங்குத்து வட்ட இயக்கம்
எடுத்துக்காட்டு 4.17
கயிற்றுடன் கட்டப்பட்ட ஒரு வாளியில் உள்ள நீர் 0.5 m ஆரமுள்ள செங்குத்து வட்டத்தை சுற்றி சுழற்றப்படுகிறது. இயக்கத்தின் போது நீரானது வாளியில் இருந்து சிந்தாமல் இருக்க அடிப்புள்ளியில் இருக்க வேண்டிய சிறும் திசைவேகத்தைக் கணக்கிடுக. (g = 10 ms-2)
தீர்வு
