11வது இயற்பியல் : அலகு 4 : வேலை, ஆற்றல் மற்றும் திறன்
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: ஆற்றல்
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் இயக்க ஆற்றல்
எடுத்துக்காட்டு 4.7
2 kg மற்றும் 4 kg நிறை கொண்ட இரு பொருள்கள் 20 kg ms-1 என்ற சம உந்தத்துடன் இயங்குகின்றன.
(a) அவை சம இயக்க ஆற்றலைப் பெற்றிருக்குமா?
(b) அவை சம வேகத்தைப் பெற்றிருக்குமா?
தீர்வு
(a) பொருளின் இயக்க ஆற்றல்

KE1 ≠ KE2 என அறியவும். அதாவது இருபொருட்களும் சம உந்தத்தைப் பெற்றிருந்தாலும் அவற்றின் இயக்க ஆற்றல் சமமல்ல. கனமான பொருள் இலேசான பொருளை விட குறைவான இயக்க ஆற்றலைப் பெற்றுள்ளது. ஏனென்றால் கொடுக்கப்பட்ட உந்தத்திற்கு இயக்க ஆற்றலானது நிறைக்கு எதிர் விகிதத்தில் உள்ளது.
KE ∝ 1/m
(b) உந்தம் p = mv என்பதால் இரு பொருட்களும் சம வேகத்தைப் பெற்றிருக்காது.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் நிலை ஆற்றல்
எடுத்துக்காட்டு 4.8
2 kg நிறையுள்ள பொருள் தரையிலிருந்து 5 m உயரத்திற்குக் கொண்டு செல்லப்படுகிறது (g = 10 m s-2) எனில்
a) பொருளினுள் சேமிக்கப்பட்டுள்ள நிலையாற்றல் யாது?
b) இந்த நிலையாற்றல் எங்கிருந்து கிடைத்தது?
c) பொருளை அந்த உயரத்திற்கு எடுத்துச் செல்ல எவ்வளவு புறவிசை செயல்பட வேண்டும்?
d) பொருளானது 'h' உயரத்திற்கு எடுத்துச் செல்லப்படும் போது அதன் மீது செயல்படும் நிகர விசை யாது?
தீர்வு:
a) நிலையாற்றல் U=m g h = 2 × 10 × 5 = 100 J இங்கு நேர்க்குறியானது பொருளினுள் ஆற்றல் சேமிக்கப்பட்டுள்ளதைக் குறிக்கிறது.
b) இந்த நிலையாற்றலானது, புற விசையை செயல்படுத்தும் வெளிப்புற அமைப்பிலிருந்து பொருளுக்கு மாற்றப்பட்டுள்ளது.
c) பொருளை 5 m உயரத்திற்கு எடுத்துச் செல்ல செயல்படுத்தப்பட்ட புற விசை ![]() ஆனது
ஆனது 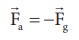
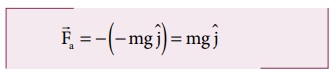
![]() ஆனது செங்குத்தாக மேல்நோக்கிய திசையில் செயல்படும் ஓரலகு வெக்டர் ஆகும்.
ஆனது செங்குத்தாக மேல்நோக்கிய திசையில் செயல்படும் ஓரலகு வெக்டர் ஆகும்.
d) நிலையாற்றலின் வரையறையில் இருந்து, பொருளானது மாறாத் திசைவேகத்தில் நகர்த்தப்பட வேண்டும். எனவே, பொருளின் மீது செயல்படும் நிகர விசை சுழி ஆகும்.
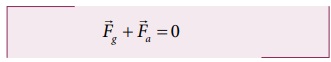
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் மீட்சி நிலை ஆற்றல்
எடுத்துக்காட்டு 4.9
இரு சுருள்வில்கள் A மற்றும் B யின் சுருள்மாறிலிகள் kA > kB என்றவாறு உள்ளன. அவை சம விசைகளால் நீட்சியடையச் செய்யப்பட்டால் எந்த சுருள்வில்லின் மீது அதிக வேலை செய்யப்பட வேண்டும்?
தீர்வு
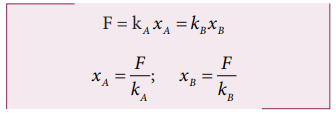
சுருள்வில்கள் மீது செய்யப்பட்ட வேலை சுருள்வில்களில் நிலை ஆற்றலாக சேமிக்கப்படுகிறது.

kA > kB, குறிப்பது UB > UA ஆகும். எனவே A - வை விட B - இன் மீது அதிக வேலை செய்யப்பட வேண்டும்.
எடுத்துக்காட்டு 4.10
m நிறையுள்ள ஒரு பொருள் சுருள்வில்லுடன் இணைக்கப்பட்டு, செயல்படுத்தப்படும் விசையினால் அது நடுநிலையில் இருந்து 25 cm அளவிற்கு நீட்சியடைகிறது.
(a) சுருள்வில் - நிறை அமைப்பில் சேமிக்கப்பட்ட நிலை ஆற்றலைக் கணக்கிடுக.
(b) இந்த நீட்சியில் சுருள்வில் விசையால் செய்யப்பட்ட வேலை யாது?
(c) சுருள்வில்லானது அதே 25 cm அளவிற்கு அமுக்கப்பட்டால் சேமிக்கப்படும் நிலை ஆற்றல் மற்றும் அமுக்கத்தின் போது சுருள்வில் விசையால் செய்யப்பட்ட வேலை ஆகியவற்றைக் கணக்கிடுக. (சுருள்வில் மாறிலி k = 0.1 N m-1)
தீர்வு
சுருள்வில் மாறிலி k = 0.1 Nm-1
இடப்பெயர்ச்சி x = 25 cm = 0.25 m
(a) சுருள்வில்லில் சேமிக்கப்பட்ட நிலை ஆற்றல்
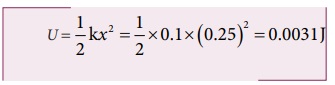
(b) சுருள்வில் விசை ![]() ஆல் செய்யப்பட்ட வேலை Ws மதிப்பு
ஆல் செய்யப்பட்ட வேலை Ws மதிப்பு
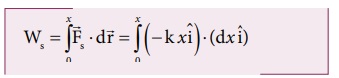
சுருள்வில்விசை ![]() எதிர்க்குறி x அச்சின் திசையில் செயல்படுகிறது. அதேசமயம் நீட்சியானது நேர்க்குறி x அச்சின் திசையில் செயல்படுகிறது.
எதிர்க்குறி x அச்சின் திசையில் செயல்படுகிறது. அதேசமயம் நீட்சியானது நேர்க்குறி x அச்சின் திசையில் செயல்படுகிறது.
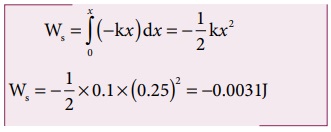
வெளிப்புற அமைப்பால் செய்யப்பட்ட வேலையின் மூலம் நிலை ஆற்றலை வரையறுக்கலாம். நிலை ஆற்றலில் உள்ள நேர்க்குறி, ஆற்றலானது அமைப்பிலிருந்து பொருளுக்கு மாற்றப்படுவதைக் குறிக்கிறது. ஆனால் இந்நேர்வில் மீள் விசையால் செய்யப்பட்ட வேலை எதிர்க்குறி மதிப்புடையது. ஏனென்றால் மீள்விசையானது இடப்பெயர்ச்சியின் திசைக்கு எதிர்த்திசையில் செயல்படுகிறது.
(c) அமுக்கத்தின் போதும் பொருளில் அதே அளவு நிலை ஆற்றல் சேமிக்கப்படுகிறது.
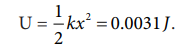
அமுக்கப்படும் போது சுருள்வில் மீள் விசையால் செய்யப்பட்ட வேலை
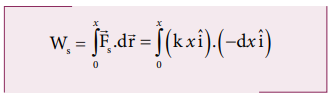
அமுக்கப்படும் நேர்வில் சுருள்வில் மீள்விசை நேர்க்குறி x அச்சை நோக்கி செயல்படுகிறது. மற்றும் இடப்பெயர்ச்சியானது எதிர்க்குறி x அச்சின் திசையில் உள்ளது.
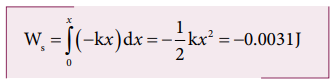
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகள்
எடுத்துக்காட்டு 4.11
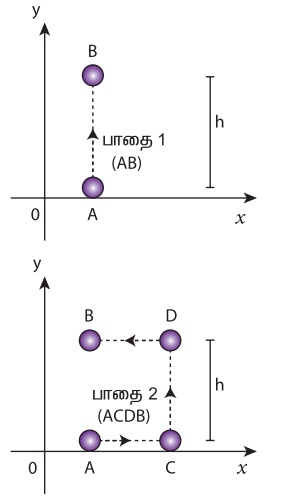
கீழ்கண்ட நேர்வுகளில் புவியீர்ப்பு விசையினால் செய்யப்பட்ட வேலையைக் கணக்கிடுக.
தீர்வு
விசை 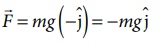
இடப்பெயர்ச்சி வெக்டர் 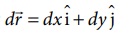
(இடப்பெயர்ச்சி இரு பரிமாணத்தில் உள்ளதால் அலகு வெக்டர்கள் ![]() மற்றும்
மற்றும் ![]() பயன்படுத்தப்படுகிறது)
பயன்படுத்தப்படுகிறது)
(a) இயக்கமானது செங்குத்தாக மட்டும் உள்ளதால், இடப்பெயர்ச்சியின் கிடைத்தளக்கூறு dx சுழியாகும். எனவே பாதை 1 இன் வழியே விசையினால் செய்யப்பட்ட வேலை (h தொலைவிற்கு)
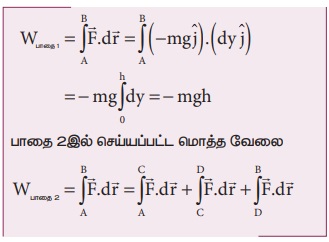
ஆனால்
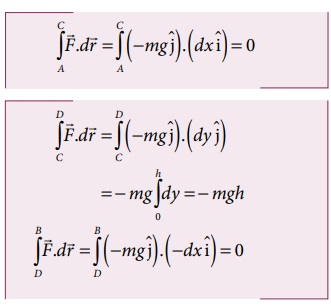
எனவே பாதை 2 இன் வழியே விசையினால் செய்யப்பட்ட மொத்த வேலை
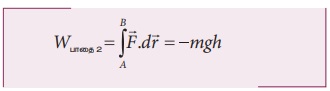
ஆற்றல் மாற்றா விசையினால் செய்யப்பட்ட வேலை பாதையைச் சார்ந்ததல்ல என்பதை அறியவும்.
எடுத்துக்காட்டு 4.12
2 kg நிறையுள்ள ஒரு பொருள் இயக்க உராய்வுக் குணகம் 0.9 கொண்டுள்ள ஒரு பரப்பில் 20 N புறவிசையினால் 10 m தொலைவிற்கு நகர்த்தப்படுவதாகக் கருதுக. புறவிசை மற்றும் இயக்க உராய்வினால் செய்யப்பட்ட வேலை என்ன? முடிவைப் பற்றிய கருத்தைக் கூறுக (g = 10 ms-2 எனக் கொள்க)
தீர்வு
m = 2 kg, d = 10 m, Fext = 20 N, µk = 0.9
ஒரு பொருள் கிடைமட்டப் பரப்பில் இயங்கும்போது அது இரு விசைகளைப் பெறுகிறது.
(a) புற விசை Fext = 20 N
(b) இயக்க உராய்வு விசை
fk = μk mg = 0.9 × (2) × 10 = 18N.
புறவிசையினால் செய்யப்பட்ட வேலை
Wext = Fd = 20 × 10 = 200 J
இயக்க உராய்வு விசையினால் செய்யப்பட்ட வேலை
Wk = fkd = (-18) × 10 = -180 J
இங்கு எதிர்க்குறியானது இயக்க உராய்வு விசை, இடப்பெயர்ச்சியின் திசைக்கு எதிராக உள்ளதைக் குறிக்கிறது.
பொருளின் மீது செய்யப்பட்ட மொத்த வேலை
Wtotal = Wext + Wk = 200 - 180 = 20 J
உராய்வு விசை ஒரு ஆற்றல் மாற்றும் விசை என்பதால் புறவிசையால் கொடுக்கப்பட்ட 200 J இல் 180 J இழக்கப்பட்டது மற்றும் இதனை மீட்டெடுக்க இயலாது.
எடுத்துக்காட்டு 4.13
1 kg நிறையுள்ள ஒரு பொருள் h = 10 m உயரத்திலிருந்து விழுகிறது.
(a) h = 10 m உயரத்தில் பொருளின் மொத்த ஆற்றல்
(b) h = 4 m உயரத்தில் பொருளின் நிலை ஆற்றல்
(c) h = 4 m உயரத்தில் பொருளின் இயக்க ஆற்றல்
(d) பொருள் தரையில் மோதும் வேகம் ஆகியவற்றைக் கணக்கிடுக.
(g = 10 ms-2 எனக் கொள்க)
தீர்வு
(a) புவியீர்ப்பு விசை ஆற்றல் மாற்றா விசையாகும். எனவே இயக்கம் முழுவதும் மொத்த ஆற்றல் மாறாமல் இருக்கும்.
h = 10 m உயரத்தில் மொத்த ஆற்றல் (E) முழுவதும் நிலை ஆற்றலாக இருக்கும்.
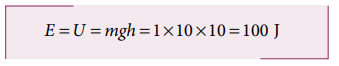
(b) h = 4 m உயரத்தில் நிலை ஆற்றல்
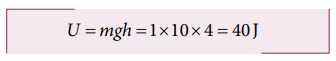
(c) இயக்கம் முழுவதும் மொத்த ஆற்றல் மாறிலி என்பதால் h = 4 m உயரத்தில் இயக்க ஆற்றலானது
KE = E - U = 100 - 40 = 60J
மாறாக 4 m உயரத்தில் பொருளின் திசைவேகத்தில் இருந்தும் இயக்க ஆற்றலைக் காணலாம். 6 m வீழ்ந்த பிறகு உள்ள திசைவேகத்தை இயக்கச் சமன்பாட்டிலிருந்து கணக்கிடலாம்.
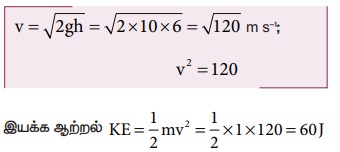
(d) பொருள் தரையில் மோதும் நிலையில் மொத்த ஆற்றல் முழுவதும் இயக்க ஆற்றலாகும். மேலும் நிலை ஆற்றல் U = 0
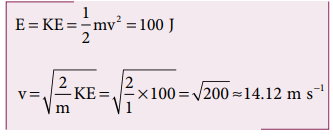
எடுத்துக்காட்டு 4.14
படத்தில் காட்டியுள்ளவாறு 100 kg நிறையுள்ள ஒரு பொருள் தரையிலிருந்து 10 m உயரத்திற்கு இரு மாறுபட்ட வழிகளில் தூக்கப்படுகிறது. இரு நேர்வுகளிலும் புவியீர்ப்பால் செய்யப்பட்ட வேலை என்ன? சாய்தளத்தின் வழியாக பொருளை எடுத்துச் செல்வது எளிதாக உள்ளது ஏன்?
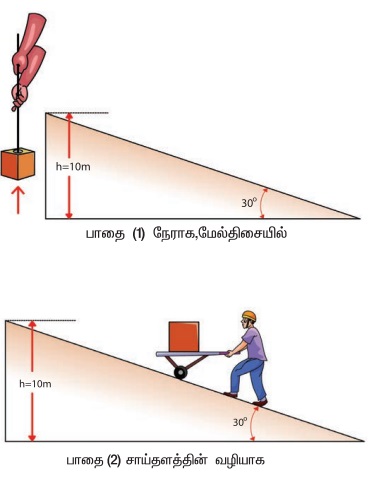
தீர்வு
m = 100 kg, h = 10 m
பாதை (1) இன் வழியே:
பொருளை 10 m உயரத்திற்குத் தூக்கத் தேவையான சிறும் விசை F1 ஆனது புவியீர்ப்பு விசைக்குச் சமமாக இருக்க வேண்டும்.
F1 = mg = 100 × 10 = 1000 N
பாதை (1) இன் வழியே நகர்ந்த தொலைவு h = 10 m
பாதை (1) இன் வழியே பொருளின் மீது செய்யப்பட்ட வேலை
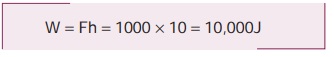
பாதை (2) இன் வழியே:
சாய்தளத்தின் வழியே பொருளைக் கொண்டு செல்ல பொருளின் மீது நாம் செலுத்தும் சிறும விசை F2 ஆனது mg-க்கு சமமாக இல்லை, மாறாக mg sin θ -க்கு சமமாகும். இங்கு θ = 30°
mg sin θ = 100 × 10 × sin30°
= 100 × 10 × 0.5 = 500 N
எனவே (mg sin θ < mg)
சாய்தளப் பாதையின் நீளமானது
l = h/sin30° = 10/0.5 = 20m
பாதை (2) இன் வழியே பொருளின் மீது செய்யப்பட்ட
வேலை W = F2 l = 500 × 20 = 10,000 J
புவியீர்ப்பு விசையானது ஆற்றல் மாற்றா விசை என்பதால் புவியீர்ப்பால் பொருளின் மீது செய்யப்பட்ட வேலை அதனை கொண்டு சென்ற பாதையைச் சார்ந்ததல்ல.
இரு பாதைகளிலும் புவியீர்ப்பு விசையால் செய்யப்பட்ட வேலை 10,000 J ஆகும்.
பாதை (1) இன் வழியே:
குறைவான தொலைவு நகர்த்த புவியீர்ப்புக்கு எதிராக அதிகமான விசை செலுத்த வேண்டியுள்ளது.
பாதை (2) இன் வழியே:
அதிகமான தொலைவு நகர்த்த புவியீர்ப்புக்கு எதிராக குறைவான விசை செலுத்த வேண்டியுள்ளது.
சாய்தளத்தின் வழியே செலுத்தப்பட வேண்டிய விசை குறைவாக உள்ளதால் சாய்தளத்தின் வழியாக பொருளை எடுத்துச் செல்வது எளிதாக உள்ளது.
எடுத்துக்காட்டு 4.15
m நிறையுள்ள ஒரு பொருள் தரையிலிருந்து V0 என்ற தொடக்க வேகத்துடன் எறியப்படுகிறது. h உயரத்தில் அதன் வேகத்தைக் காண்க.
தீர்வு
புவியீர்ப்பு விசை ஆற்றல் மாற்றா விசை என்பதால் இயக்கம் முழுவதும் மொத்த ஆற்றல் மாறாது.
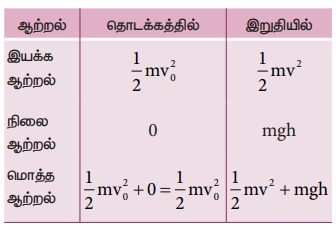
h உயரத்தில் நிலை ஆற்றல், இயக்க ஆற்றல் மற்றும் மொத்த ஆற்றல் ஆகியவற்றின் இறுதி மதிப்புகள் கணக்கிடப்பட்டுள்ளன.
ஆற்றல் மாறா விதியின் படி தொடக்க மற்றும் இறுதி மொத்த ஆற்றல்கள் சமமாகும்.
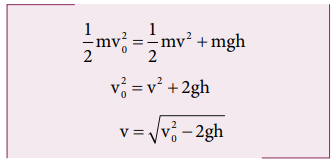
பாடப்பகுதி (2.11.2) இல் இயக்கவியல் சமன்பாட்டைப் பயன்படுத்தி நுண்கணித முறைப்படி இது போன்ற முடிவு பெறப்பட்டதை கவனிக்கவும். எனினும் ஆற்றல் மாறா விதியின் முறைப்படி கணக்கிடுவது நுண்கணித முறையைவிட மிகவும் எளிதாக உள்ளது.
எடுத்துக்காட்டு 4.16
ஒரு சுருள்வில்லுடன் இணைக்கப்பட்ட 2 kg நிறையுள்ள ஒரு பொருள் அதன் சமநிலையிலிருந்து x = 10 m என்ற தொலைவுக்கு நகர்த்தப்படுகிறது. சுருள்வில் மாறிலி k = 1 N m-1 மற்றும் பரப்பு உராய்வற்றதாகக் கருதுக.
(a) பொருளானது சமநிலையைக் கடக்கும்போது அதன் வேகம் என்ன?
(b) பொருளானது சமநிலையைக் கடக்கும் போதும், x = ± 10 m என்ற விளிம்பு நிலையை கடக்கும்போதும் பொருளின் மீது செயல்படும் விசை யாது?
தீர்வு
(a) சுருள்வில் விசை ஒரு ஆற்றல் மாற்றா விசை ஆகையால் மொத்த ஆற்றல் மாறிலி ஆகும். x = 10 m எனும்போது மொத்த ஆற்றல் ழுமுவதும் நிலை ஆற்றலாக மட்டுமே இருக்கும்.
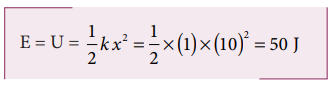
பொருள் சமநிலையைக் கடக்கும்போது (x = 0) நிலை ஆற்றலானது
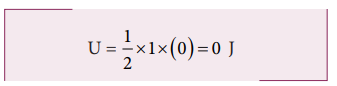
இந்நிலையில் முழு ஆற்றலும் இயக்க ஆற்றலாக மட்டுமே உள்ளது.
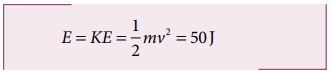
வேகம்
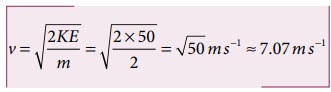
(b) சுருள்வில்லின் மீள்விசை F = – kx என்பதால் பொருளானது நடுநிலையைக் கடக்கும் போது அது எவ்விசையையும் உணராது. நடுநிலையில் பொருளானது மிக வேகமாக நகருகிறது என்பதை அறியவும். பொருளானது x = +10 m (நீட்சி) என்ற நிலையில் உள்ள போது விசை F = - k x
F = - (1) (10) = - 10 N இங்கு எதிர்க்குறியானது விசை நடுநிலையை நோக்கி, அதாவது எதிர் x அச்சை நோக்கி உள்ளதைக் குறிக்கிறது. மேலும் பொருளானது
x = -10 m (அமுக்கம்) என்ற நிலையில் உள்ளபோது அது உணரும் விசை
F = - (1) (-10) = + 10 N. இங்கு நேர்க்குறியானது விசை நேர் x - அச்சை நோக்கி உள்ளதைக் குறிக்கிறது.
x = ±10 m என்ற நிலையில் பொருளானது இந்த இரு விளிம்பு புள்ளிகளிலும் பெரும் விசையை உணர்ந்தாலும் கணநேர ஓய்வு நிலைக்கு வருகிறது.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் செங்குத்து வட்ட இயக்கம்
எடுத்துக்காட்டு 4.17
கயிற்றுடன் கட்டப்பட்ட ஒரு வாளியில் உள்ள நீர் 0.5 m ஆரமுள்ள செங்குத்து வட்டத்தை சுற்றி சுழற்றப்படுகிறது. இயக்கத்தின் போது நீரானது வாளியில் இருந்து சிந்தாமல் இருக்க அடிப்புள்ளியில் இருக்க வேண்டிய சிறும் திசைவேகத்தைக் கணக்கிடுக. (g = 10 ms-2)
தீர்வு
