செங்குத்து வட்ட இயக்கம்

செங்குத்து வட்ட இயக்கம் [Motion in a vertical circle] 

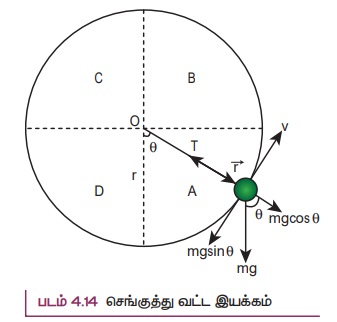
m நிறையுள்ள ஒரு பொருள் நிறையற்ற, நீட்சித் தன்மையற்ற நூலின் ஒரு முனையில் இணைக்கப்படுகிறது. மேலும், நூலின் மறுமுனையானது நிலையாக இருக்குமாறு பொருத்தப்பட்டுள்ளது. அந்தப்பொருள் செங்குத்துத் தளத்தில் அமைந்த வட்ட இயக்கத்தை மேற்கொள்வதாகக் கருதுவோம். நூலின் நீளமானது வட்டப்பாதையின் ஆரமாக () உள்ளது. (படம் 4.14) படத்தில் காட்டியுள்ளவாறு பொருளின் இயக்கத்தைப் பற்றி அறிய தனித்த பொருளின் விசைப்படம் (Free body diagram) ஒன்றைக் கருதுவோம். இங்கு நிலை வெக்டர் () ஆனது செங்குத்தான கீழ்நோக்கிய திசையுடன் θ கோணத்தை ஏற்படுத்தி படத்தில் உள்ளவாறு உடனடி திசைவேகத்தைக் கொண்டுள்ளது. 

பொருளின் மீது இரு விசைகள் செயல்படுகின்றன. 

1. கீழ் நோக்கி செயல்படும் புவியீர்ப்பு விசை 

2. நூலின் வழியே செயல்படும் இழுவிசை

பொருளின் மீது நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்த, தொடுகோட்டுத் திசையில், 

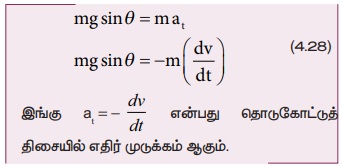
ஆரத்திசையில்,

இயக்கத்தை நன்கு புரிந்து கொள்ளும் வகையில் வட்டத்தை A, B, C, D என்ற நான்கு பகுதிகளாகப் பிரிக்கலாம். மேற்கண்ட இரு சமன்பாடுகளில் இருந்து கீழ்க்கண்டவாறு நான்கு முக்கிய கருத்துகளைப் புரிந்து கொள்ளலாம். 

(i) பொருளானது அனைத்து θ மதிப்புக்களுக்கும் (θ = 0° தவிர) தொடுகோட்டுத் திசையில் முடுக்கத்தை (g sin θ) கொண்டிருக்கிறது. இந்த செங்குத்து வட்ட இயக்கம் ஒரு சீரான வட்ட இயக்கம் அல்ல என்பது தெளிவாகிறது. 

(ii) சமன்பாடுகள் (4.28) மற்றும் (4.29) இல் இருந்து அறிந்து கொள்வது என்னவெனில் இயக்கத்தின் போது திசைவேகத்தின் எண் மதிப்பு மாறுவதால், நூலின் இழுவிசையும் மாறுகின்றது. 

(iii) சமன்பாடு (4.29), T = mg cos θ + mv2/r சுட்டிக்காட்டுவது வட்டத்தின் A மற்றும் D பகுதிகளில் (–π/2 < θ < π/2 மற்றும் cos θ நேர்க்குறி) mg cos θ எப்போதும் சுழியைவிட அதிகமாகும். எனவே திசைவேகம் சுழியானாலும் இழுவிசை சுழியாகாது.

(iv) சமன்பாடு (4.29), mv2/r = T - mg cosθ மேலும் சுட்டிக்காட்டுவது வட்டத்தின் B மற்றும் C பகுதிகளில் (–π/2 < θ < 3π/2 மற்றும் cosθ எதிர்க்குறி), சமன்பாட்டின் இரண்டாவது பகுதி (- mg cos θ) எப்போதும் சுழியை விட அதிகமாகும். எனவே இழுவிசை சுழியானாலும் திசைவேகம் சுழியாகாது. 

செங்குத்து வட்ட இயக்கம் தொடர்பான கணக்குகளை தீர்வுகாணும்போது மேற்கண்ட கருத்துக்களை மனதில் கொள்ள வேண்டும். 

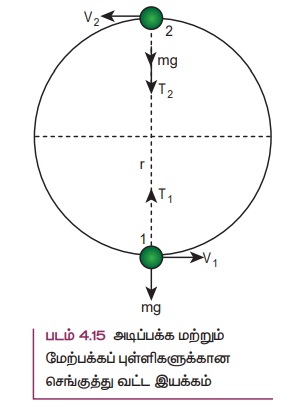
படம் 4.15 இல் காட்டியுள்ளவாறு அடிப்பக்கப் புள்ளி 1 மற்றும் மேற்பக்கப் புள்ளி 2 ஆகிய இரு நிலைகளை மட்டும் கருத்தில் கொண்டு மேலும் பகுப்பாய்வு செய்வோம். பொருளின் திசைவேகமானது அடிப்பக்கப்புள்ளி 1 இல் எனவும், மேற்பக்கப் புள்ளி 2 இல் எனவும் வேறு எந்த புள்ளியிலும் எனவும் கொள்க. திசைவேகத்தின் திசை அனைத்துப் புள்ளிகளிலும் வட்டப்பாதையின் தொடுகோட்டுத் திசையில் உள்ளது. அடிப்பக்கப் புள்ளியிலிருந்து நூலின் இழுவிசையானது எனவும், மேற்பக்கப் புள்ளியிலிருந்து இழுவிசை எனவும் வேறு எந்த புள்ளியிலும் இழுவிசை எனவும் கொள்க. ஒவ்வொரு புள்ளியிலும் இழுவிசை மையப்புள்ளியை நோக்கி செயல்படுகிறது. ஆற்றல் மாறா விதியைப் பயன்படுத்தி இந்த இரு புள்ளிகளிலும் இழுவிசைகள் மற்றும் திசைவேகங்களைக் கணக்கிடலாம்.

அடிப்பக்கப் புள்ளி (1): 

பொருளானது அடிப்பக்கப் புள்ளி 1 இல் உள்ள போது புவியீர்ப்பு விசை m   பொருளின் மீது செங்குத்தாக கீழ்நோக்கி செயல்படுகிறது மற்றும் இழுவிசை 1 செங்குத்தாக மேல்நோக்கி அதாவது மையப்புள்ளியை நோக்கிச் செயல்படுகிறது. சமன்பாடு (4.29) இல் இருந்து நாம் பெறுவது

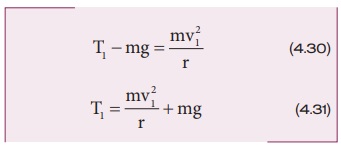
மேற்பக்கப் புள்ளி (2): 

மேற்பக்கப் புள்ளி 2 இல் பொருளின் மீதான புவியீர்ப்பு விசை m மற்றும் இழுவிசை 2 ஆகிய இரண்டும் கீழ்நோக்கி அதாவது மையப்புள்ளியை நோக்கி செயல்படுகிறது.

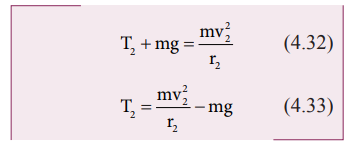
சமன்பாடுகள் (4.31) மற்றும் (4.33) இல் இருந்து T1 > T2 என அறியலாம். இழுவிசையின் வேறுபாடு T1 – T2 ஆனது சமன்பாடு (4.33)ஐ சமன்பாடு (4.31) இல் இருந்து கழிப்பதன் மூலம் பெறப்படுகிறது.

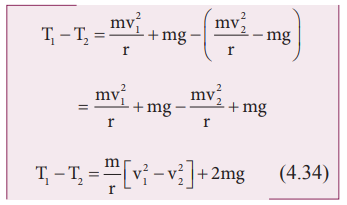
புள்ளி 1 மற்றும் 2 இல் ஆற்றல் மாறா விதியைப் பயன்படுத்தி [v12 – v22] மதிப்பை எளிதாகக் கணக்கிடலாம்.

இழுவிசையும் பொருள் செல்லும் திசையும் எப்போதும் ஒன்றுக்கொன்று செங்குத்தாக உள்ளதால் இழுவிசையானது பொருளின்மீது எவ்வித வேலையும் செய்யாது. 

புவியீர்ப்பு விசையானது பொருளின் மீது வேலை செய்கிறது. மேலும் அது ஆற்றல் மாற்றா விசை என்பதால் இயக்கம் முழுவதும் பொருளின் மொத்த ஆற்றல் மாறாது.

புள்ளி 1 இல் நிலை ஆற்றல் U1 = 0 (புள்ளி 1 ஐ குறிப்புப் புள்ளியாக எடுத்துக்கொள்வதன் மூலம்) புள்ளி 1 இல் இயக்க ஆற்றல்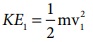

புள்ளி 1 இல் மொத்த ஆற்றல்

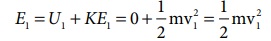
இதுபோன்றே புள்ளி 2 இல் நிலை ஆற்றல் U2 = mg (2r) 

(புள்ளி 1 இல் இருந்து h மதிப்பு 2r ஆகும்)

புள்ளி 2 இல் இயக்க ஆற்றல்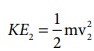

புள்ளி 2 இல் மொத்த ஆற்றல்

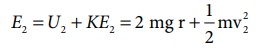
சமன்பாடு (4.35) இல் உள்ளவாறு ஆற்றல் மாறா விதிப்படி

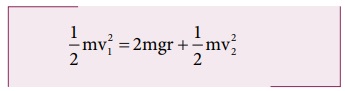
மாற்றியமைக்க

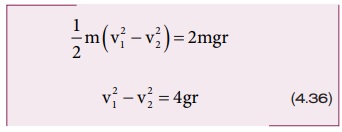
சமன்பாடு (4.34) இல் சமன்பாடு (4.36) ஐ பிரதியிட

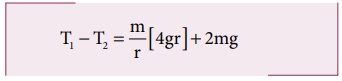
எனவே இழுவிசையில் மாறுபாடானது

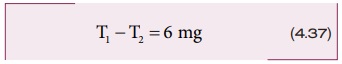
மேற்பக்கப் புள்ளி (2) இல் சிறும் வேகம்: 

பொருளானது புள்ளி 2 இல் ஒரு சிறும் வேகத்தைக் கொண்டிருக்க வேண்டும், இல்லையெனில் புள்ளி 2 ஐ அடையும் முன்பாக நூலானது தளர்வுற்று அதனால் பொருள் வட்டப்பாதையை நிறைவு செய்யாது. இந்த சிறும் வேகத்தைக் கணக்கிட சமன்பாடு (4.33) இல் இழுவிசை T2 = 0 எனக் கொள்வோம்.

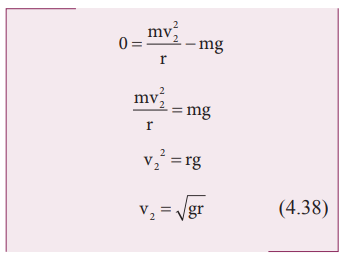
பொருளானது வட்டப்பாதையில் தொடர்ந்து இயங்க புள்ளி 2 இல் v2 ≥ √gr என்ற வேகத்தைக் கொண்டிருக்க வேண்டும். 

அடிப்புள்ளி (1) இல் சிறும் வேகம்: 

புள்ளி 2 இல் இந்த சிறும வேகத்தைப் (v2=√gr) பெற பொருளானது புள்ளி 1லும் ஒரு சிறும் வேகத்தைக் கொண்டிருக்க வேண்டும். 

சமன்பாடு (4.36) ஐப் பயன்படுத்தி புள்ளி 1 இல் சிறும் வேகத்தை நாம் காணலாம்.

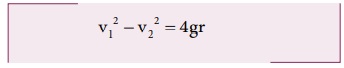
சமன்பாடு (4.38) ஐ (4.36) இல் பிரதியிட

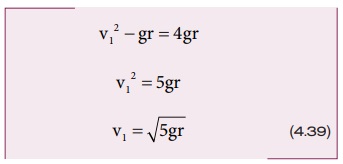
பொருளானது வட்டப்பாதையில் தொடர்ந்து இயங்க புள்ளி 1 இல் (v1≥√5gr) என்ற வேகத்தைக் கொண்டிருக்க வேண்டும். 

சமன்பாடுகள் (4.38) மற்றும் (4.39) இல் இருந்து அறிவது என்னவெனில் பொருள் வட்டப்பாதையை விட்டு விலகாமல் நிறைவு செய்ய அடிப்புள்ளி 1 இல் சிறும் வேகமானது மேற்பக்கப் புள்ளி 2 இல் உள்ள சிறும் வேகத்தை விட √5 மடங்கு இருக்க வேண்டும்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் செங்குத்து வட்ட இயக்கம்

எடுத்துக்காட்டு 4.17

கயிற்றுடன் கட்டப்பட்ட ஒரு வாளியில் உள்ள நீர் 0.5 m ஆரமுள்ள செங்குத்து வட்டத்தை சுற்றி சுழற்றப்படுகிறது. இயக்கத்தின் போது நீரானது வாளியில் இருந்து சிந்தாமல் இருக்க அடிப்புள்ளியில் இருக்க வேண்டிய சிறும் திசைவேகத்தைக் கணக்கிடுக. (g = 10 ms-2)

தீர்வு