11வது இயற்பியல் : அலகு 4 : வேலை, ஆற்றல் மற்றும் திறன்
ஆற்றல் மாறா விதி
ஆற்றல் மாறா விதி (Law of Conservation of energy)
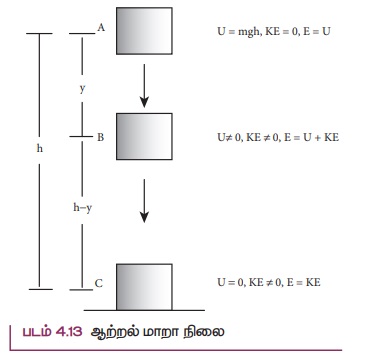
ஒரு பொருளை நாம் மேல்நோக்கி எறிந்தால் அதன் இயக்க ஆற்றல் குறைந்து கொண்டே செல்கிறது மற்றும் அதன் நிலை ஆற்றல் அதிகரித்துக் கொண்டே செல்கிறது (காற்றுத் தடையை புறக்கணிக்கும்போது). பொருளானது பெரும உயரத்தை அடையும்போது ஆற்றல் முழுவதும் நிலை ஆற்றலாகும். அதுபோன்று பொருளானது பெரும் உயரத்தில் இருந்து விழுந்தால் அதன் இயக்க ஆற்றல் அதிகரிக்கும் மற்றும் நிலை ஆற்றல் குறையும். தரையைத் தொடும்போது அதன் ஆற்றல் முழுவதும் இயக்க ஆற்றலாகும். படம் 4.13 இல் காட்டியுள்ளவாறு இடைப்பட்ட புள்ளிகளில் ஆற்றலானது இயக்க ஆற்றலாகவும் நிலை ஆற்றலாகவும் இருக்கும். பொருளானது தரையை அடையும் போது இயக்க ஆற்றல் முழுவதுமாக ஒலி, வெப்பம், ஒளி மற்றும் பொருளின் உருக்குலைவு போன்ற வேறுவகை ஆற்றலாக வெளிப்படும்.
இந்த உதாரணத்தில் ஒவ்வொரு புள்ளியிலும் நிலையாற்றல் மற்றும் இயக்க ஆற்றல் மாறும். எனினும், இயக்க ஆற்றல் மற்றும் நிலை ஆற்றலின் கூடுதல் அதாவது மொத்த இயந்திர ஆற்றல் எப்போதும் மாறாது. இது மொத்த ஆற்றல் மாறாது என்பதைக் குறிக்கிறது. இதுவே ஆற்றல் மாறா விதியாகும்.
ஆற்றல் மாறா விதியின்படி ஆற்றலை ஆக்கவோ அழிக்கவோ இயலாது. ஆற்றலானது ஒரு வகையிலிருந்து மற்றொரு வகையாக மாறக்கூடியது. ஆனால் ஒரு தனித்த அமைப்பின் மொத்த ஆற்றல் மாறிலியாக இருக்கும்.
படம் 4.13 விளக்குவது யாதெனில், h உயரத்தில் ஓய்வில் உள்ள ஒரு பொருளின் மொத்த ஆற்றல் முழுவதும் நிலை ஆற்றல் (U=mgh) மட்டுமே. மேலும் h உயரத்தில் அதன் இயக்க ஆற்றல் (KE) சுழியாகும். பொருள் கீழே விழும்போது ‘y’ தொலைவில் அதன் நிலையாற்றல் மற்றும் இயக்க ஆற்றல் சுழியாகாது. அதேசமயம் h உயரத்தில் இருந்த அதே அளவில் மொத்த ஆற்றல் மாறாமல் இருக்கும். பொருள் தரையைத் தொட நெருங்கும் போது நிலை ஆற்றல் சுழியாகும் மற்றும் மொத்த ஆற்றல் இயக்க ஆற்றலாக மட்டுமே இருக்கும்.
எடுத்துக்காட்டு 4.13
1 kg நிறையுள்ள ஒரு பொருள் h = 10 m உயரத்திலிருந்து விழுகிறது.
(a) h = 10 m உயரத்தில் பொருளின் மொத்த ஆற்றல்
(b) h = 4 m உயரத்தில் பொருளின் நிலை ஆற்றல்
(c) h = 4 m உயரத்தில் பொருளின் இயக்க ஆற்றல்
(d) பொருள் தரையில் மோதும் வேகம் ஆகியவற்றைக் கணக்கிடுக.
(g = 10 ms-2 எனக் கொள்க)
தீர்வு
(a) புவியீர்ப்பு விசை ஆற்றல் மாற்றா விசையாகும். எனவே இயக்கம் முழுவதும் மொத்த ஆற்றல் மாறாமல் இருக்கும்.
h = 10 m உயரத்தில் மொத்த ஆற்றல் (E) முழுவதும் நிலை ஆற்றலாக இருக்கும்.
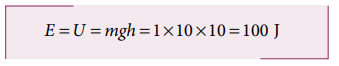
(b) h = 4 m உயரத்தில் நிலை ஆற்றல்
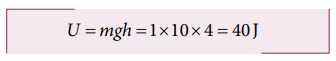
(c) இயக்கம் முழுவதும் மொத்த ஆற்றல் மாறிலி என்பதால் h = 4 m உயரத்தில் இயக்க ஆற்றலானது
KE = E - U = 100 - 40 = 60J
மாறாக 4 m உயரத்தில் பொருளின் திசைவேகத்தில் இருந்தும் இயக்க ஆற்றலைக் காணலாம். 6 m வீழ்ந்த பிறகு உள்ள திசைவேகத்தை இயக்கச் சமன்பாட்டிலிருந்து கணக்கிடலாம்.
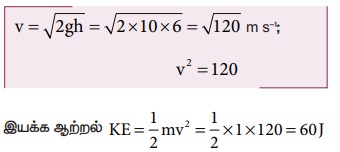
(d) பொருள் தரையில் மோதும் நிலையில் மொத்த ஆற்றல் முழுவதும் இயக்க ஆற்றலாகும். மேலும் நிலை ஆற்றல் U = 0
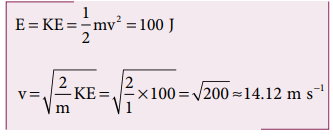
எடுத்துக்காட்டு 4.14
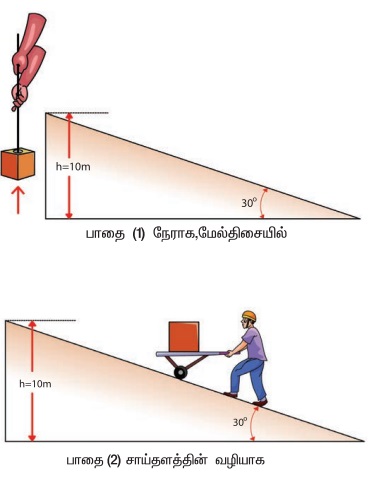
படத்தில் காட்டியுள்ளவாறு 100 kg நிறையுள்ள ஒரு பொருள் தரையிலிருந்து 10 m உயரத்திற்கு இரு மாறுபட்ட வழிகளில் தூக்கப்படுகிறது. இரு நேர்வுகளிலும் புவியீர்ப்பால் செய்யப்பட்ட வேலை என்ன? சாய்தளத்தின் வழியாக பொருளை எடுத்துச் செல்வது எளிதாக உள்ளது ஏன்?
தீர்வு
m = 100 kg, h = 10 m
பாதை (1) இன் வழியே:
பொருளை 10 m உயரத்திற்குத் தூக்கத் தேவையான சிறும் விசை F1 ஆனது புவியீர்ப்பு விசைக்குச் சமமாக இருக்க வேண்டும்.
F1 = mg = 100 × 10 = 1000 N
பாதை (1) இன் வழியே நகர்ந்த தொலைவு h = 10 m
பாதை (1) இன் வழியே பொருளின் மீது செய்யப்பட்ட வேலை
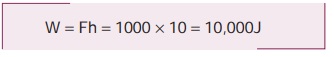
பாதை (2) இன் வழியே:
சாய்தளத்தின் வழியே பொருளைக் கொண்டு செல்ல பொருளின் மீது நாம் செலுத்தும் சிறும விசை F2 ஆனது mg-க்கு சமமாக இல்லை, மாறாக mg sin θ -க்கு சமமாகும். இங்கு θ = 30°
mg sin θ = 100 × 10 × sin30°
= 100 × 10 × 0.5 = 500 N
எனவே (mg sin θ < mg)
சாய்தளப் பாதையின் நீளமானது
l = h/sin30° = 10/0.5 = 20m
பாதை (2) இன் வழியே பொருளின் மீது செய்யப்பட்ட
வேலை W = F2 l = 500 × 20 = 10,000 J
புவியீர்ப்பு விசையானது ஆற்றல் மாற்றா விசை என்பதால் புவியீர்ப்பால் பொருளின் மீது செய்யப்பட்ட வேலை அதனை கொண்டு சென்ற பாதையைச் சார்ந்ததல்ல.
இரு பாதைகளிலும் புவியீர்ப்பு விசையால் செய்யப்பட்ட வேலை 10,000 J ஆகும்.
பாதை (1) இன் வழியே:
குறைவான தொலைவு நகர்த்த புவியீர்ப்புக்கு எதிராக அதிகமான விசை செலுத்த வேண்டியுள்ளது.
பாதை (2) இன் வழியே:
அதிகமான தொலைவு நகர்த்த புவியீர்ப்புக்கு எதிராக குறைவான விசை செலுத்த வேண்டியுள்ளது.
சாய்தளத்தின் வழியே செலுத்தப்பட வேண்டிய விசை குறைவாக உள்ளதால் சாய்தளத்தின் வழியாக பொருளை எடுத்துச் செல்வது எளிதாக உள்ளது.
எடுத்துக்காட்டு 4.15
m நிறையுள்ள ஒரு பொருள் தரையிலிருந்து V0 என்ற தொடக்க வேகத்துடன் எறியப்படுகிறது. h உயரத்தில் அதன் வேகத்தைக் காண்க.
தீர்வு
புவியீர்ப்பு விசை ஆற்றல் மாற்றா விசை என்பதால் இயக்கம் முழுவதும் மொத்த ஆற்றல் மாறாது.
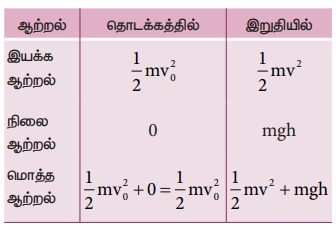
h உயரத்தில் நிலை ஆற்றல், இயக்க ஆற்றல் மற்றும் மொத்த ஆற்றல் ஆகியவற்றின் இறுதி மதிப்புகள் கணக்கிடப்பட்டுள்ளன.
ஆற்றல் மாறா விதியின் படி தொடக்க மற்றும் இறுதி மொத்த ஆற்றல்கள் சமமாகும்.
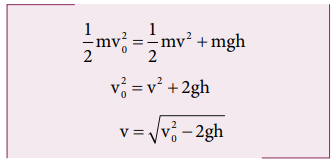
பாடப்பகுதி (2.11.2) இல் இயக்கவியல் சமன்பாட்டைப் பயன்படுத்தி நுண்கணித முறைப்படி இது போன்ற முடிவு பெறப்பட்டதை கவனிக்கவும். எனினும் ஆற்றல் மாறா விதியின் முறைப்படி கணக்கிடுவது நுண்கணித முறையைவிட மிகவும் எளிதாக உள்ளது.
எடுத்துக்காட்டு 4.16
ஒரு சுருள்வில்லுடன் இணைக்கப்பட்ட 2 kg நிறையுள்ள ஒரு பொருள் அதன் சமநிலையிலிருந்து x = 10 m என்ற தொலைவுக்கு நகர்த்தப்படுகிறது. சுருள்வில் மாறிலி k = 1 N m-1 மற்றும் பரப்பு உராய்வற்றதாகக் கருதுக.
(a) பொருளானது சமநிலையைக் கடக்கும்போது அதன் வேகம் என்ன?
(b) பொருளானது சமநிலையைக் கடக்கும் போதும், x = ± 10 m என்ற விளிம்பு நிலையை கடக்கும்போதும் பொருளின் மீது செயல்படும் விசை யாது?
தீர்வு
(a) சுருள்வில் விசை ஒரு ஆற்றல் மாற்றா விசை ஆகையால் மொத்த ஆற்றல் மாறிலி ஆகும். x = 10 m எனும்போது மொத்த ஆற்றல் ழுமுவதும் நிலை ஆற்றலாக மட்டுமே இருக்கும்.
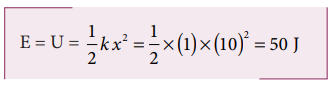
பொருள் சமநிலையைக் கடக்கும்போது (x = 0) நிலை ஆற்றலானது
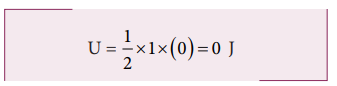
இந்நிலையில் முழு ஆற்றலும் இயக்க ஆற்றலாக மட்டுமே உள்ளது.
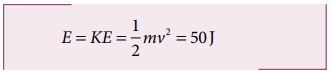
வேகம்
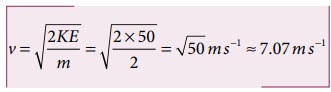
(b) சுருள்வில்லின் மீள்விசை F = – kx என்பதால் பொருளானது நடுநிலையைக் கடக்கும் போது அது எவ்விசையையும் உணராது. நடுநிலையில் பொருளானது மிக வேகமாக நகருகிறது என்பதை அறியவும். பொருளானது x = +10 m (நீட்சி) என்ற நிலையில் உள்ள போது விசை F = - k x
F = - (1) (10) = - 10 N இங்கு எதிர்க்குறியானது விசை நடுநிலையை நோக்கி, அதாவது எதிர் x அச்சை நோக்கி உள்ளதைக் குறிக்கிறது. மேலும் பொருளானது
x = -10 m (அமுக்கம்) என்ற நிலையில் உள்ளபோது அது உணரும் விசை
F = - (1) (-10) = + 10 N. இங்கு நேர்க்குறியானது விசை நேர் x - அச்சை நோக்கி உள்ளதைக் குறிக்கிறது.
x = ±10 m என்ற நிலையில் பொருளானது இந்த இரு விளிம்பு புள்ளிகளிலும் பெரும் விசையை உணர்ந்தாலும் கணநேர ஓய்வு நிலைக்கு வருகிறது.