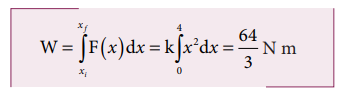தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: வேலை மற்றும் விசையினால் செய்யப்பட்ட வேலை

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் வேலை

எடுத்துக்காட்டு 4.1 

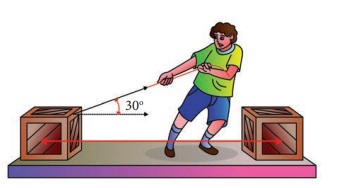
ஒரு பெட்டி 25 N விசையினால் 15 m இடப்பெயர்ச்சி ஏற்படுமாறு இழுக்கப்படுகிறது. விசைக்கும் இடப்பெயர்ச்சிக்கும் இடையே உள்ள கோணம் 30° எனில் விசையினால் செய்யப்பட்ட வேலையைக் காண்க.

தீர்வு 

விசை F = 25 N 

இடப்பெயர்ச்சி dr = 15 m

F மற்றும் dr இடையே உள்ள கோணம் θ = 30o 

செய்யப்பட்ட வேலை W = F dr cosθ

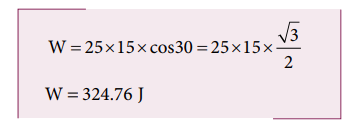
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் மாறா விசையினால் செய்யப்பட்ட வேலை

எடுத்துக்காட்டு 4.2 

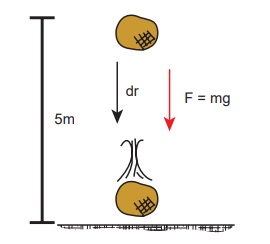
2 kg நிறையுள்ள ஒரு பொருள் 5 m உயரத்தில் இருந்து தரையில் விழுகிறது. புவியீர்ப்பு விசையினால் பொருளின் மீது செய்யப்பட்டவேலை என்ன? (காற்றின் தடையைப் புறக்கணிக்கவும். புவியீர்ப்பு முடுக்கம் g = 10 m s-2 எனக் கொள்க)

தீர்வு 

இந்நேர்வில் பொருளின் மீது செயல்படும் விசை கீழ் நோக்கிய புவியீர்ப்பு விசை ஆகும். இது மாறா விசையாகும். 

புவியீர்ப்பு விசையினால் செய்யப்பட்ட வேலை

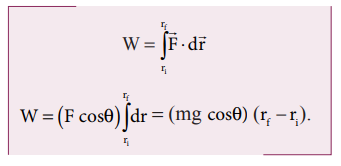
மேலும் பொருளானது படத்தில் காட்டியுள்ளவாறு கீழ்நோக்கிய புவியீர்ப்பு விசையின் (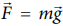) திசையில் நகருகிறது. எனவே, அவற்றிற்கிடையே உள்ள கோணம் θ = 0°, cos0° = 1 மற்றும் இடப்பெயர்ச்சி (rf - ri ) = 5 m

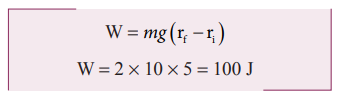
எனவே பொருளின் மீது செயல்படும் புவியீர்ப்பு விசையினால் செய்யப்பட்ட வேலை நேர்க்குறி மதிப்பைப் பெறுகிறது.

எடுத்துக்காட்டு 4.3 

படத்தில் காட்டியுள்ளவாறு நிறை m = 1 kg கொண்ட ஒரு பொருள் θ = 30° சாய்வுக்கோணம் கொண்ட 10 m நீளமுள்ள உராய்வற்ற தளத்தில் மேலிருந்து கீழ்நோக்கிச் சறுக்குகிறது. புவியீர்ப்பு விசை மற்றும் செங்குத்து விசையினால் பொருளின் மீது செய்யப்பட்ட வேலையைக் கணக்கிடுக. புவியீர்ப்பு முடுக்கம் (g) = 10 m s−2 எனக் கருதுக.

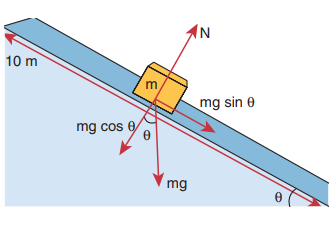
தீர்வு: 

சாய்வுத்தளத்தில் பொருள் அடையும் முடுக்கம் = g sinθ என முந்தைய பாடப்பகுதியில் கணக்கிட்டுள்ளோம். 

நியூட்டனின் இரண்டாம் விதிப்படி, சாய்வுத்தளத்தில் பொருளின்மீது செயல்படும் விசை F = mg sinθ. இந்த விசையானது பொருளின் இயக்கம் முழுவதும் மாறாது என்பதை அறியவும். 

புவியீர்ப்பு விசையின் சாய் வுத்தளத் தின் கிடைத்தளக் கூறினால் (mg sinθ) செய்யப்பட்ட வேலை

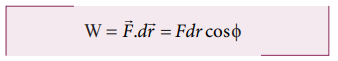
இங்கு ϕ என்பது விசை (mg sinθ) மற்றும் பொருள் செல்லும் திசைக்கு (dr) இடையே உள்ள கோணமாகும். இந்நேர்வில், விசை (mg sinθ) மற்றும் இடப்பெயர்ச்சி   ஆகியவை ஒரே திசையில் உள்ளன. எனவே ϕ = 0° மற்றும் cos ϕ = 1

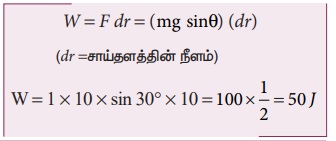
mg cos θ என்ற கூறு மற்றும் செங்குத்து விசை N ஆகியவை பொருள் செல்லும் திசைக்குச் செங்குத்தாக உள்ளதால் அவை எந்த வேலையும் செய்யாது.

எடுத்துக்காட்டு 4.4 

மேல்நோக்கி எறியப்பட்ட 2 kg நிறையுள்ள ஒரு பொருள் 5 m உயரத்தை அடைந்து பின்னர் தரையில் வந்து விழுகிறது (காற்றுத்தடையைப் புறக்கணிக்கவும்) எனில் பின்வருவனவற்றை கணக்கிடுக. 

(a) பொருள் 5 m உயரத்தை அடையும்போது புவியீர்ப்பு விசையால் செய்யப்பட்ட வேலை 

(b) பொருள் மீண்டும் தரையை அடையும்போது புவியீர்ப்பு விசையால் செய்யப்பட்ட வேலை 

(c) புவியீர்ப்பு விசையினால் மேல்நோக்கிய மற்றும் கீழ்நோக்கிய இயக்கத்தில் செய்யப்பட்ட மொத்தவேலை மற்றும் முடிவின் இயற்பியல் முக்கியத்துவத்தைக் குறிப்பிடுக.

தீர்வு 

பொருள் மேல்நோக்கிச் செல்லும்போது இடப்பெயர்ச்சி மேல்நோக்கிய திசையிலும் பொருளின் மீது செயல்படும் புவியீர்ப்பு விசை கீழ்நோக்கிய திசையிலும் செயல்படுகின்றன. எனவே இடப்பெயர்ச்சிக்கும் புவியீர்ப்பு விசைக்கும் இடையே உள்ள கோணம் 180° ஆகும். 

(a) மேல்நோக்கிய இயக்கத்தில் புவியீர்ப்பு விசையினால் செய்யப்பட்ட வேலை 

இங்கு dr = 5 m மற்றும் F = mg

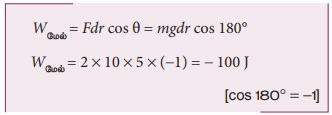
(b) பொருள் கீழ்நோக்கி விழும்போது புவியீர்ப்பு விசை மற்றும் இடப்பெயர்ச்சி இரண்டும் ஒரே திசையில் உள்ளன. இதன் மூலம் புவியீர்ப்பு விசைக்கும் இடப்பெயர்ச்சிக்கும் இடையே உள்ள கோணம் θ = 0° என அறியலாம்.

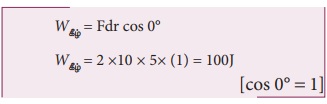
(c) பொருளின் முழு பயணத்தின் போது (மேல்நோக்கிய மற்றும் கீழ் நோக்கிய இயக்கம்) புவியீர்ப்பு விசையினால் செய்யப்பட்ட மொத்த வேலை

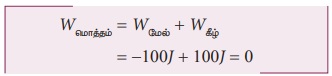
புவியீர்ப்பு விசையானது பொருளிற்கு எவ்வித ஆற்றலையும் மாற்றவில்லை என்பதை இது குறிக்கிறது. பொருள் மேல்நோக்கி எறியப்படும்போது புறக்காரணிகளால் பொருளுக்கு ஆற்றல் அளிக்கப்படுகிறது. பொருள் திரும்ப வந்து தரையில் மோதும்போது பொருள் பெற்ற ஆற்றலானது புவிப்பரப்பிற்கு மாற்றப்படுகிறது (தரையினுள் செல்கிறது)

எடுத்துக்காட்டு 4.5 

ஒரு பளு தூக்குபவர் 250 kg நிறையை 5000 N விசையால் 5 m உயரத்திற்கு தூக்குகிறார். 

(a) பளுதூக்குபவரால் செய்யப்பட்ட வேலை என்ன? 

(b) புவியீர்ப்பு விசையால் செய்யப்பட்ட வேலை என்ன? 

(c) பொருளின் மீது செய்யப்பட்ட நிகர வேலை என்ன? 

தீர்வு 

(a) பளுதூக்குபவர் நிறையைத் தூக்கும்போது விசையும் இடப்பெயர்ச்சியும் ஒரே திசையில் உள்ளதால் அவற்றிற்கிடையே உள்ள கோணம் θ = 0°. எனவே பளுதூக்குபவரால் செய்யப்பட்ட வேலை

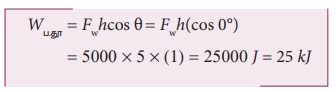
(b) பளுதூக்குபவர் நிறையைத் தூக்கும்போது புவியீர்ப்புவிசை கீழ்நோக்கி செயல்படுவதால் விசையும் இடப்பெயர்ச்சியும் எதிரெதிர் திசையில் உள்ளன. எனவே அவற்றிற்கிடையே உள்ள கோணம்  θ = 180°.

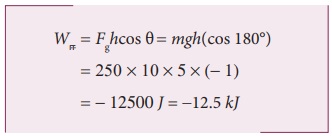
(c) பொருளின் மீது செய்யப்பட்ட நிகர வேலை (மொத்த வேலை)

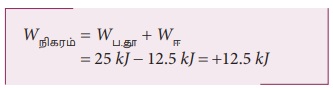
தீர்க்கப்பட்ட எடுத்துக்காட்டு மாறுபடும் விசையினால் செய்யப்பட்ட வேலை

எடுத்துக்காட்டு 4.6

தொடக்கத்தில் ஓய்வில் உள்ள ஒரு பொருளின் மீது F = kx2 என்ற மாறும் விசை செயல்படுகிறது. பொருளானது x = 0 m முதல் x = 4 m வரை இடப்பெயர்ச்சி அடைய விசையினால் செய்யப்பட்ட வேலையைக் கணக்கிடுக. (மாறிலி k = 1 N m-2 எனக்கருதுக) 

தீர்வு

செய்யப்பட்ட வேலை