தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகள்

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் ஆற்றல் மாற்றா மற்றும் ஆற்றல் மாற்றும் விசைகள்

எடுத்துக்காட்டு 4.11

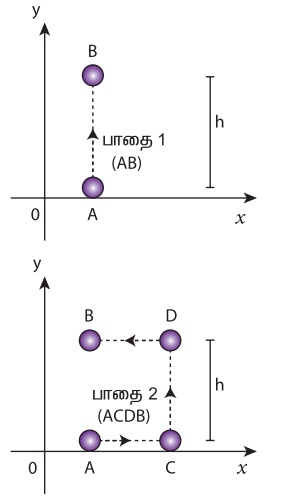
கீழ்கண்ட நேர்வுகளில் புவியீர்ப்பு விசையினால் செய்யப்பட்ட வேலையைக் கணக்கிடுக.

தீர்வு

விசை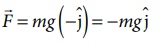

இடப்பெயர்ச்சி வெக்டர்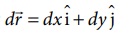

(இடப்பெயர்ச்சி இரு பரிமாணத்தில் உள்ளதால் அலகு வெக்டர்கள் மற்றும் பயன்படுத்தப்படுகிறது)

(a) இயக்கமானது செங்குத்தாக மட்டும் உள்ளதால், இடப்பெயர்ச்சியின் கிடைத்தளக்கூறு dx சுழியாகும். எனவே பாதை 1 இன் வழியே விசையினால் செய்யப்பட்ட வேலை (h தொலைவிற்கு)

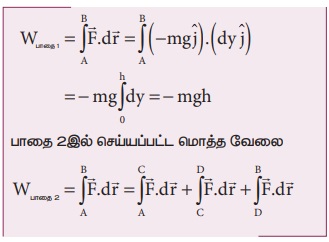
ஆனால்

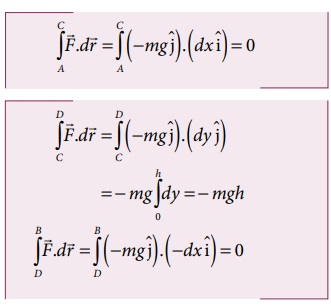
எனவே பாதை 2 இன் வழியே விசையினால் செய்யப்பட்ட மொத்த வேலை

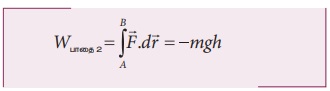
ஆற்றல் மாற்றா விசையினால் செய்யப்பட்ட வேலை பாதையைச் சார்ந்ததல்ல என்பதை அறியவும்.

எடுத்துக்காட்டு 4.12

2 kg நிறையுள்ள ஒரு பொருள் இயக்க உராய்வுக் குணகம் 0.9 கொண்டுள்ள ஒரு பரப்பில் 20 N புறவிசையினால் 10 m தொலைவிற்கு நகர்த்தப்படுவதாகக் கருதுக. புறவிசை மற்றும் இயக்க உராய்வினால் செய்யப்பட்ட வேலை என்ன? முடிவைப் பற்றிய கருத்தைக் கூறுக (g = 10 ms-2 எனக் கொள்க)

தீர்வு

m = 2 kg, d = 10 m, Fext = 20 N, µk = 0.9 

ஒரு பொருள் கிடைமட்டப் பரப்பில் இயங்கும்போது அது இரு விசைகளைப் பெறுகிறது. 

(a) புற விசை Fext = 20 N 

(b) இயக்க உராய்வு விசை

fk = μk mg = 0.9 × (2) × 10 = 18N. 

புறவிசையினால் செய்யப்பட்ட வேலை

Wext = Fd = 20 × 10 = 200 J 

இயக்க உராய்வு விசையினால் செய்யப்பட்ட வேலை 

Wk = fkd = (-18) × 10 = -180 J

இங்கு எதிர்க்குறியானது இயக்க உராய்வு விசை, இடப்பெயர்ச்சியின் திசைக்கு எதிராக உள்ளதைக் குறிக்கிறது.

பொருளின் மீது செய்யப்பட்ட மொத்த வேலை 

Wtotal = Wext + Wk = 200 - 180 = 20 J 

உராய்வு விசை ஒரு ஆற்றல் மாற்றும் விசை என்பதால் புறவிசையால் கொடுக்கப்பட்ட 200 J இல் 180 J இழக்கப்பட்டது மற்றும் இதனை மீட்டெடுக்க இயலாது.