Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї | Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ѕЯ«цЯ«▓Я»Ї | 10th Mathematics : UNIT 4 : Geometry
10Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 4 : Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї
Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ѕЯ«цЯ«▓Я»Ї
Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ѕЯ«цЯ«▓Я»Ї (Construction of triangle)
Я««Я»ЂЯ«еЯ»ЇЯ«цЯ»ѕЯ«» Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«хЯ«░Я»ѕЯ«хЯ«цЯ»Ђ Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї
(i) Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї, Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«еЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ
(ii) Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї, Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ
(iii) Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї, Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»ЂЯ«џЯ««Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕЯ«џЯ»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐
Я«єЯ«ЋЯ«┐Я«»Я«Е Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«хЯ«░Я»ѕЯ«хЯ«цЯ»Ђ Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«хЯ«░Я»ѕЯ«цЯ«▓Я»ѕ Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«ЋЯ»ІЯ«БЯ««Я»Ї ╬И-Я«хЯ»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ЄЯ«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«хЯ«ЪЯ»ЇЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕ Я«хЯ«░Я»ѕЯ«цЯ«▓Я»Ї
Я«хЯ«░Я»ѕЯ««Я»ЂЯ«▒Я»ѕ
Я«фЯ«ЪЯ«┐ 1: ![]() Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«Ћ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 2: Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ A-Я«»Я«┐Я«▓Я»Ї РѕаBAE = ╬И Я«јЯ«Е Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я«ЙЯ«▒Я»Ђ AE Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 3: AF Рћ┤ AE Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 4: AB-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ѕЯ«»Я«ЋЯ»Ї Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ«ЙЯ«ЕЯ«цЯ»Ђ AF-Я«»Я»ѕ O-Я«»Я«┐Я«▓Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«фЯ«ЪЯ«┐ 5: O-Я«хЯ»ѕ Я««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, OA-Я«хЯ»ѕ Я«єЯ«░Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ, Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 6: Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ЇЯ««Я»ЄЯ«▓Я»Ї Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ C Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ї Я«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ»єЯ«░Я«┐Я«» Я«хЯ«┐Я«▓Я»Ї ACB Я«єЯ«ЕЯ«цЯ»Ђ Я«ЋЯ»ІЯ«БЯ««Я»Ї ╬И - Я«хЯ»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«хЯ«ЪЯ»ЇЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
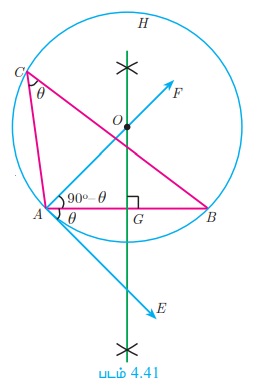
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
C1, C2,... Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, ╬ћBAC1 , ╬ћBAC2,... Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«њЯ«░Я»Є Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»ЂЯ««Я»Ї, Я«њЯ«░Я»Є Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ««Я»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї, Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«цЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«хЯ«░Я»ѕЯ«цЯ«▓Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.17
PQ = 8 Я«џЯ»є.Я««Я»ђ, РѕаR = 60┬░ Я«ЅЯ«џЯ»ЇЯ«џЯ«┐ R-Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ PQ-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї RG = 5.8 Я«џЯ»є.Я««Я»ђ. Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ ╬ћPQR Я«хЯ«░Я»ѕЯ«Ћ. R-Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ PQ-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
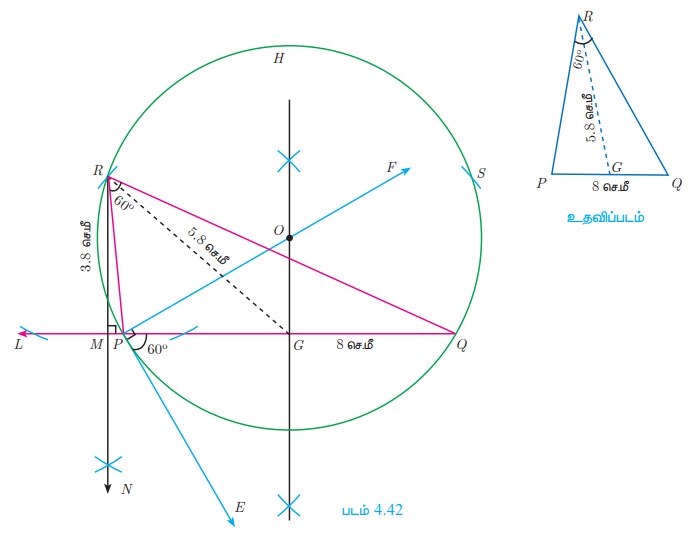
Я«хЯ«░Я»ѕЯ««Я»ЂЯ«▒Я»ѕ
Я«фЯ«ЪЯ«┐ 1: PQ = 8Я«џЯ»є.Я««Я»ђ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 2: Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ P Я«хЯ«┤Я«┐Я«»Я»Є РѕаQPE = 60┬░ Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐ PE Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐: 3 Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ P Я«хЯ«┤Я«┐Я«»Я»Є РѕаEPF = 90┬░ Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐ PF Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 4: PQ-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ PF-Я«љ O-Я«хЯ«┐Я«▓Я»ЂЯ««Я»Ї, PQ-Я«љ G-Я«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«фЯ«ЪЯ«┐ 5: O-Я«хЯ»ѕ Я««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, OP-Я«»Я»ѕ Я«єЯ«░Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 6: G-Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 5.8 Я«џЯ»є.Я««Я»ђ Я«єЯ«░Я««Я»ЂЯ«│Я»ЇЯ«│ Я«хЯ«┐Я«▓Я»ЇЯ«ЋЯ«│Я»ѕ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«хЯ«░Я»ѕЯ«Ћ. Я«ЁЯ«хЯ»ѕ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ R Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї S Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Я«фЯ«ЪЯ«┐ 7: PR Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї RQ -Я«љ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. ╬ћPQR Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«фЯ«ЪЯ«┐ 8: R-Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ LQ-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ RN Я«хЯ«░Я»ѕЯ«Ћ. RN Я«єЯ«ЕЯ«цЯ»Ђ LQ - Я«хЯ»ѕ M-Я«»Я«┐Я«▓Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«фЯ«ЪЯ«┐ 9: Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ RM-Я«»Я«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 3.8 Я«џЯ»є.Я««Я»ђ.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ ╬ћPQS Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї, Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«цЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«хЯ«░Я»ѕЯ«цЯ«▓Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.18
QR = 5 Я«џЯ»є.Я««Я»ђ, РѕаP = 30┬░ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї P-Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ QR-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 4.2 Я«џЯ»є.Я««Я»ђ Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ ╬ћPQR Я«хЯ«░Я»ѕЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
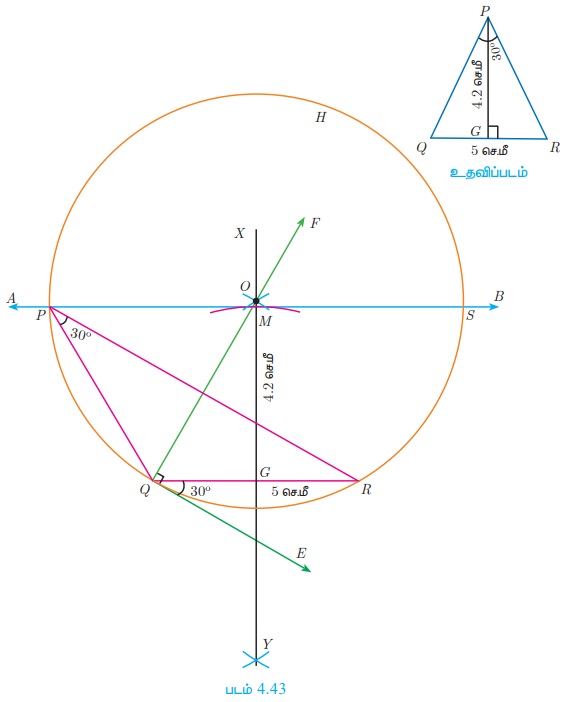
Я«хЯ«░Я»ѕЯ««Я»ЂЯ«▒Я»ѕ
Я«фЯ«ЪЯ«┐ 1: QR = 5 Я«џЯ»є.Я««Я»ђ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 2: Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Q Я«хЯ«┤Я«┐Я«»Я»Є РѕаRQE = 30┬░ Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐ QE Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 3: Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Q Я«хЯ«┤Я«┐Я«»Я»Є РѕаEQF = 90┬░ Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐ QF Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 4: QR-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ XY-Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ QF-Я«љ O-Я«хЯ«┐Я«▓Я»ЂЯ««Я»Ї, QR-Я«љ G-Я«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«фЯ«ЪЯ«┐ 5: O-Я«хЯ»ѕ Я««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, OQ - Я«хЯ»ѕ Я«єЯ«░Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 6: G-Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я««Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ XY-Я«▓Я»Ї M Я«хЯ«┤Я«┐Я«»Я»Є GM = 4.2 Я«џЯ»є.Я««Я»ђ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐ Я«њЯ«░Я»Ђ Я«хЯ«┐Я«▓Я»Ї Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 7: QR-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ M Я«хЯ«┤Я«┐Я«»Я»Є AB Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 8: AB-Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ P Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї S -Я«»Я«┐Я«▓Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ
Я«фЯ«ЪЯ«┐ 9: QP Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї RP -Я«»Я»ѕ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. ╬ћPQR Я«єЯ«ЕЯ«цЯ»Ђ Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ ╬ћSQR Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї, Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»ЂЯ«џЯ««Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«цЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«хЯ«░Я»ѕЯ«цЯ«▓Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.19
Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї BC = 8 Я«џЯ»є.Я««Я»ђ, РѕаA = 60┬░ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї РѕаA-Я«»Я«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»ЂЯ«џЯ««Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ BC-Я«љ D Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї BD = 6 Я«џЯ»є.Я««Я»ђ Я«јЯ«ЕЯ»ЇЯ«▒Я«хЯ«ЙЯ«▒Я»Ђ Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї ABC Я«хЯ«░Я»ѕЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
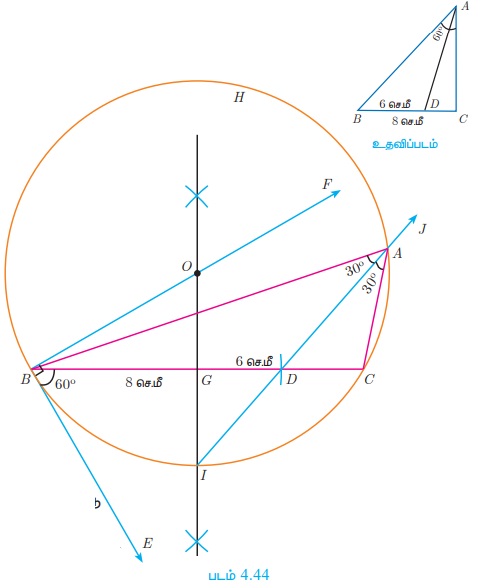
Я«хЯ«░Я»ѕЯ««Я»ЂЯ«▒Я»ѕ
Я«фЯ«ЪЯ«┐ 1: BC = 8 Я«џЯ»є.Я««Я»ђ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 2: Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ B Я«хЯ«┤Я«┐Я«»Я»Є РѕаCBE = 60┬░ Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐ BE Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 3: Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ B Я«хЯ«┤Я«┐Я«»Я»Є РѕаEBF = 90┬░ Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐ BF Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 4: BC-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ«ЙЯ«ЕЯ«цЯ»Ђ BF-Я«љ O-Я«хЯ«┐Я«▓Я»ЂЯ««Я»Ї, BC-Я«»Я»ѕ G-Я«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«фЯ«ЪЯ«┐ 5: O - Я«хЯ»ѕ Я««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, OB-Я«»Я»ѕ Я«єЯ«░Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 6: Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ B -Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ BC-Я«»Я«┐Я«▓Я»Ї 6 Я«џЯ»є.Я««Я»ђ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї D Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«┐Я«▓Я»Ї Я«хЯ«░Я»ѕЯ«Ћ.
Я«фЯ«ЪЯ«┐ 7: Я««Я»ѕЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ I Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. ID-Я«»Я»ѕ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Я«фЯ«ЪЯ«┐ 8: ID-Я«»Я»ѕ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї A-Я«»Я«┐Я«▓Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«еЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ«хЯ»ЂЯ««Я»Ї. AB Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї AC-Я«»Я»ѕ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. ╬ћABC Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.