Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»Ђ, Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї, Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї | Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї - Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї | 10th Mathematics : UNIT 4 : Geometry
10Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 4 : Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї
Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї
Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї (Pythagoras Theorem)
Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї, Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»ЇЯ«цЯ«ЙЯ«ЕЯ»Ї Я««Я«┐Я«ЋЯ«хЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я««Я«ЙЯ«ЕЯ«цЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї Я«ЄЯ«цЯ»Ђ Я«ЁЯ«цЯ«┐Я«Ћ Я«ЁЯ«│Я«хЯ«┐Я«▓Я«ЙЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ 350-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«Е Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я«ЄЯ«еЯ»ЇЯ«ц Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ«┐Я«▒Я«еЯ»ЇЯ«ц Я«ЋЯ«БЯ«┐Я«цЯ«хЯ«┐Я«»Я«▓Я«ЙЯ«│Я«░Я»ЇЯ«ЋЯ«│Я»Ї, Я«ЁЯ«▒Я«┐Я«ъЯ«░Я»ЇЯ«ЋЯ«│Я»Ї, Я«фЯ»іЯ«▒Я«┐Я«»Я«ЙЯ«│Я«░Я»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«БЯ«┐Я«ц Я«єЯ«░Я»ЇЯ«хЯ«▓Я«░Я»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ«┐Я«»Я»ІЯ«░Я«ЙЯ«▓Я»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ. Я«ЄЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ««Я»єЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«хЯ«┐Я«ЕЯ»Ї 20-Я«хЯ«цЯ»Ђ Я«юЯ«ЕЯ«ЙЯ«цЯ«┐Я«фЯ«цЯ«┐ Я«юЯ»ЄЯ««Я»ЇЯ«ИЯ»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«фЯ»ђЯ«▓Я»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«њЯ«░Я»ЂЯ«хЯ«░Я»Ї. Я«ЁЯ««Я»єЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«хЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї Я«ЋЯ«▒Я»ЇЯ«фЯ«┐Я«цЯ»ЇЯ«цЯ«▓Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«цЯ»ЄЯ«џЯ«┐Я«» Я««Я«ЕЯ»ЇЯ«▒Я««Я»Ї (NCTM) Я«хЯ»єЯ«│Я«┐Я«»Я«┐Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я«┐Я«иЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»Ї Я«▓Я»ѓЯ««Я«┐Я«ИЯ»Ї Я«јЯ«┤Я»ЂЯ«цЯ«┐Я«» "The Pythagorean Proposition" Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ«▓Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я«ЙЯ«Е Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї 367 Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е.
Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї (a, b, c) Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї (a, b, c) -Я«љ Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ»ІЯ«░Я«┐Я«»Я«ЕЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐ Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«єЯ«ЋЯ«хЯ»Є, (a, b, c) Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ»ѕ Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ»ІЯ«░Я«┐Я«»Я«ЕЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, c2 = a2 + b2 Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я«▓Я»ЇЯ«▓Я«ЙЯ«цЯ»Ђ, Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«фЯ»Ї Я«фЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї Я««Я«┐Я«ЋЯ«фЯ»Ї Я«фЯ«┐Я«░Я«фЯ«▓Я««Я«ЙЯ«ЕЯ«цЯ»ЂЯ««Я»Ї, Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ЂЯ«хЯ««Я»Ї Я«хЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«цЯ«цЯ»ЂЯ««Я«ЙЯ«Е Я«ЄЯ«цЯ»ЇЯ«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«ЋЯ«▒Я»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ 4
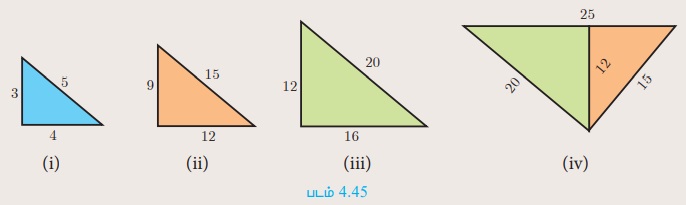
Я«фЯ«ЪЯ«┐ 1: Я«њЯ«░Я»Ђ Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«ЙЯ«│Я«┐Я«▓Я»Ї, Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (i)-Я«»Я«┐Я«▓Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«Ћ.
Я«фЯ«ЪЯ«┐ 2: Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«хЯ«БЯ»ЇЯ«Б Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«ЙЯ«│Я»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (ii)РђЊЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (i)-Я«»Я«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (iii)- Я«»Я«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (i)- Я«»Я«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (iv)-Я«»Я«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (i)-Я«»Я«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«љЯ«еЯ»ЇЯ«цЯ»Ђ Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«Ћ.
Я«фЯ«ЪЯ«┐ 3: Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (ii) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (iii)-Я«»Я«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Е Я«ЁЯ«│Я«хЯ»Ђ 12 Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЄЯ«БЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (iv)-Я«»Я«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї (iv)-Я«хЯ»ІЯ«ЪЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я«┐Я«ЕЯ»ЇЯ««Я»ђЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«џЯ«░Я«┐Я«»Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«┐Я«»Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ«░Я»ЇЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«┤Я»ЂЯ«цЯ«хЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Е Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«ЙЯ«»Я»Ї?
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Рђб Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 90┬░ (Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї)-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«цЯ«┐Я«░Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«ЋЯ«░Я»ЇЯ«БЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒Я«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Рђб Я««Я«▒Я»ЇЯ«▒ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Рђб Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я««Я«┐Я«Ћ Я«еЯ»ђЯ«│Я««Я«ЙЯ«Е Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Є Я«ЋЯ«░Я»ЇЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 5 : Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї (Pythagoras Theorem)
Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»Ђ
Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«░Я»ЇЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
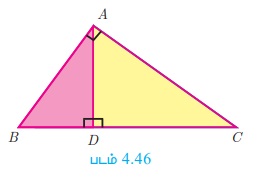
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ: ╬ћABC -Я«»Я«┐Я«▓Я»Ї РѕаA = 90┬░
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ : AB2 + AC2 = BC2
Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ : AD Рћ┤ BC Я«хЯ«░Я»ѕЯ«Ћ.
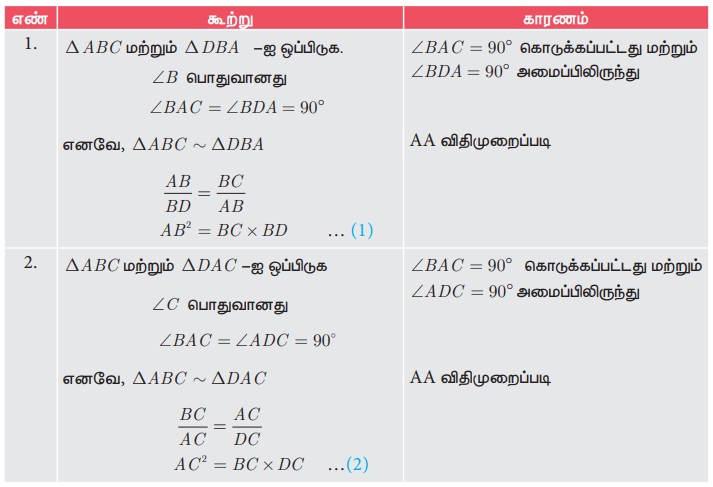
(1) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (2) -Я«љЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ««Я»Ї Я«фЯ»єЯ«▒Я»ЂЯ«хЯ«цЯ»Ђ,
AB2 + AC2 = BC ├Ќ BD + BC ├Ќ DC
= BC (BD + DC) = BC ├Ќ BC
AB2 + AC2 = BC2.
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ.
Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»єЯ«░Я«┐Я«»Я»ЂЯ««Я«Й?
Я«ЄЯ«еЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«хЯ«┐Я«▓Я»Ї Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я«ЙЯ«ЕЯ«цЯ»Ђ "Я«фЯ»їЯ«цЯ«»Я«ЙЯ«ЕЯ«Й Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї" Я«јЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«│Я««Я»Ї
1. Я«љЯ«еЯ»ЇЯ«цЯ»Ђ Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ»ІЯ«░Я«┐Я«»Я«ЕЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я»ѕ Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«Ћ.
2. Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї ------------.
Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕ (Converse of Pythagoras Theorem)
Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»Ђ
Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«еЯ»ђЯ«│Я««Я«ЙЯ«Е Я«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«│Я««Я»Ї
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я»ЂЯ««Я«Й? Я«ЈЯ«ЕЯ»Ї?
Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ 5
(i) Я«ЄЯ«░Я»Ђ Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«Ћ.
(ii) Я«ЁЯ«еЯ»ЇЯ«ц Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«ЋЯ«│Я»ѕ Я«јЯ«┤Я»ЂЯ«цЯ«┐Я«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«хЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ»Ђ p/q Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
(iii) p/q -Я«»Я«┐Я«▓Я»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ЂЯ«ЪЯ«ЕЯ»Ї 2 Я«љЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«Ъ Я«еЯ«ЙЯ««Я»Ї Я«фЯ»єЯ«▒Я»ЂЯ«хЯ«цЯ»Ђ q + 2.
(iv) Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ p, q, q + 2 Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«Ћ. Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Е?
Я«ЄЯ«еЯ»ЇЯ«цЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ, Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«юЯ»ІЯ«ЪЯ«┐ Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«цЯ»Ђ Я«фЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«фЯ«цЯ«┐Я«▓Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«Ћ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.20
Я«њЯ«░Я»Ђ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї 6 Я««Я»ђ. Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 8 Я««Я»ђ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐, Я«ЋЯ««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«еЯ«ЋЯ«░Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЋЯ««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«▒Я»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ, Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐ Я«ЋЯ««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«еЯ«ЋЯ«░Я»ЇЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐ Я«цЯ«▒Я»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«јЯ«хЯ»ЇЯ«хЯ«│Я«хЯ»Ђ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ?
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї, Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ BD = 8 Я««Я»ђ
Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї AB = 6 Я««Я»ђ
x Я««Я»ђ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«еЯ«ЋЯ«░Я»ЇЯ«еЯ»ЇЯ«ц Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ»Ђ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ««Я»Ї C Я«јЯ«ЕЯ»ЇЯ«Ћ.
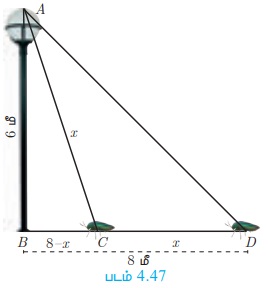
AC = CD = x Я«јЯ«ЕЯ»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї BC = BD - CD = 8 РђЊ x
╬ћABC - Я«»Я«┐Я«▓Я»Ї, РѕаB = 90┬░
AC2 = AB2 + BC 2 РЄњ x2 = 62 + (8 Рѕњ x)2
x2 = 36 + 64 Рѕњ 16x + x2
16x = 100 Я«јЯ«ЕЯ«хЯ»Є, x = 6. 25
Я«јЯ«ЕЯ«┐Я«▓Я»Ї, BC = 8 Рѕњ x = 8 Рѕњ 6.25 = 1. 75 Я««Я»ђ
Я«јЯ«ЕЯ«хЯ»Є, Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 1.75 Я««Я»ђ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.21
╬ћABC - Я«»Я«┐Я«▓Я»Ї C Я«єЯ«ЕЯ«цЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї CA Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї CB-Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є P Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Q Я«јЯ«ЕЯ«┐Я«▓Я»Ї 4(AQ2 + BP2) = 5AB2 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
╬ћAQC -Я«»Я«┐Я«▓Я»Ї, C Я«єЯ«ЕЯ«цЯ»Ђ, Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, AQ2 = AC2 + QC2 РђдРђдРђд(1)
╬ћBPC - Я«»Я«┐Я«▓Я»Ї, C Я«єЯ«ЕЯ«цЯ»Ђ, Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, BP2 = BC2 + CP2РђдРђд.(2)
╬ћABC -Я«»Я«┐Я«▓Я»Ї, C Я«єЯ«ЕЯ«цЯ»Ђ, Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, AB2 = AC2 + BC2 Рђд......(3)
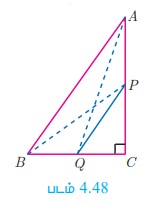
(1) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (2)- Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, AQ2 + BP2 = AC2 + QC2 + BC2 + CP2
4(AQ2 + BP2) = 4AC2 + 4QC2 + 4BC2 + 4CP2
= 4AC 2 + (2QC)2 + 4BC 2 + (2CP)2
= 4AC2 + BC2 + 4BC 2 + AC2 (PЯ««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Q Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї)
= 5(AC2 + BC2) (Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (3)-Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ)
4(AQ2 + BP2) = 5AB2
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.22
Я«џЯ»ЂЯ«хЯ«░Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 4 Я«ЁЯ«ЪЯ«┐ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЈЯ«БЯ«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«џЯ»ЂЯ«хЯ«░Я«┐Я«ЕЯ»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«»Я»ѕ 7 Я«ЁЯ«ЪЯ«┐ Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«цЯ»іЯ«ЪЯ»ЂЯ««Я»єЯ«ЕЯ«┐Я«▓Я»Ї Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«ЈЯ«БЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. Я«хЯ«┐Я«ЪЯ»ѕЯ«»Я»ѕ Я«њЯ«░Я»Ђ Я«цЯ«џЯ«« Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«Ћ Я«цЯ«░Я»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЈЯ«БЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї AB = x Я«јЯ«ЕЯ»ЇЯ«Ћ BC = 4 Я«ЁЯ«ЪЯ«┐, AC = 7 Я«ЁЯ«ЪЯ«┐.
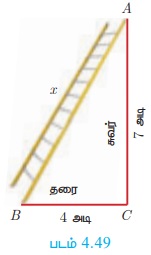
Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐, AB2 = AC2 + BC2
x2 = 72 + 42 РЄњ x2 = 49 + 16
x2 = 65. Я«јЯ«ЕЯ«хЯ»Є, x = Рѕџ65
Рѕџ65 Я«єЯ«ЕЯ«цЯ»Ђ 8 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 8.1 -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
82 = 64 < 65 < 65.61 = 8.12
Я«јЯ«ЕЯ«хЯ»Є, Я«ЈЯ«БЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ 8.1 Я«ЁЯ«ЪЯ«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 4.23
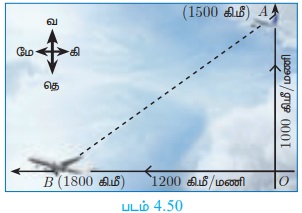
Я«њЯ«░Я»Ђ Я«хЯ«┐Я««Я«ЙЯ«ЕЯ««Я»Ї Я«хЯ«┐Я««Я«ЙЯ«Е Я«еЯ«┐Я«▓Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЄЯ«▓Я»єЯ«┤Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«хЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ 1000 Я«ЋЯ«┐.Я««Я»ђ/Я««Я«БЯ«┐ Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ«▒Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ»Є Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я«хЯ«┐Я««Я«ЙЯ«ЕЯ««Я»Ї Я«ЁЯ«цЯ»Є Я«хЯ«┐Я««Я«ЙЯ«Е Я«еЯ«┐Я«▓Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЄЯ«▓Я»єЯ«┤Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ 1200 Я«ЋЯ«┐.Я««Я»ђ/Я««Я«БЯ«┐ Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ«▒Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. 1┬й Я««Я«БЯ«┐ Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«┐Я«▒Я«ЋЯ»Ђ Я«ЄЯ«░Я»Ђ Я«хЯ«┐Я««Я«ЙЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«јЯ«хЯ»ЇЯ«хЯ«│Я«хЯ»Ђ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї?
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я««Я»ЂЯ«цЯ«▓Я»Ї Я«хЯ«┐Я««Я«ЙЯ«ЕЯ««Я»Ї O -Я«хЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ A Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Ћ. (Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ = Я«хЯ»ЄЯ«ЋЯ««Я»Ї ├Ќ Я«еЯ»ЄЯ«░Я««Я»Ї)
Я«јЯ«ЕЯ«хЯ»Є OA = ( 1000 ├Ќ 3/2 ) Я«ЋЯ«┐.Я««Я»ђ = 1500 Я«ЋЯ«┐.Я««Я»ђ.
Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«┐Я««Я«ЙЯ«ЕЯ««Я»Ї O -Я«хЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ B Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«јЯ«ЕЯ«хЯ»Є OB = (1200 ├Ќ 3/2 ) = 1800 Я«ЋЯ«┐.Я««Я»ђ.
Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«Ъ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ BA Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї AOB -Я«»Я«┐Я«▓Я»Ї, AB2 = OA2 +OB2
AB2 = (1500)2 + (1800)2 = 1002 (152 + 182)
= 1002 ├Ќ 549 = 1002 ├Ќ 9 ├Ќ 61
AB = 100 ├Ќ 3 ├Ќ Рѕџ61 = 300Рѕџ61 Я«ЋЯ«┐.Я««Я»ђ.
Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒Я«џЯ»Ї Я«џЯ»ІЯ«цЯ«ЕЯ»ѕ
1. ________________ Я«єЯ«ЕЯ«цЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я«ЙЯ«Е Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
2. Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї ___________ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
3. Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я«ЙЯ«Е Я«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ««Я»ЇЯ««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї ___________
4. Я«џЯ«░Я«┐Я«»Я«Й, Я«цЯ«хЯ«▒Я«Й Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒Я»ЂЯ«Ћ.
(i) Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«хЯ«ЋЯ»ѕ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї
(ii) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї 4 -Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.