தேல்ஸ் தேற்றமும், கோண இருசமவெட்டித் தேற்றமும்

தேல்ஸ் தேற்றமும், கோண இருசமவெட்டித் தேற்றமும் (Thales Theorem and Angle Bisector Theorem) 

அறிமுகம்

கி.மு ஏழாம் நூற்றாண்டில் வாழ்ந்த தேல்ஸ் (கி.மு. (பொ.ஆ.மு) 640-540) புகழ்பெற்ற கிரேக்கக் கணிதவியலாளரும், தத்துவஞானியும் ஆவார். கிரேக்க நாட்டில் வாழ்ந்த ஏழு ஞானிகளில் இவர் முதன்மையானவராகக் கருதப்படுகிறார். எந்த ஒரு புதிய கருத்தையும் அறிவியல் பூர்வமாகப் பரிசோதித்த பின்னரே ஏற்றுக்கொள்ள வேண்டும் என்று முதன் முதலில் அறிவித்தவர் இவரே. அந்த வகையில் இவர் கணிதத்திலும், வானியியலிலும் ஆராய்ச்சிகள் மேற்கொண்டு பல கருத்துகளைக் கண்டறிந்தார். இன்றைய அடிப்படை விகிதச்சமத் தேற்றத்தின் நிரூபணத்தை முதன்முதலில் வழங்கிய பெருமைக்குரியவர் தேல்ஸ் ஆவார். எனவே, இவருடைய பெயரால் இது "தேல்ஸ் தேற்றம்" என்று அழைக்கப்படுகிறது.

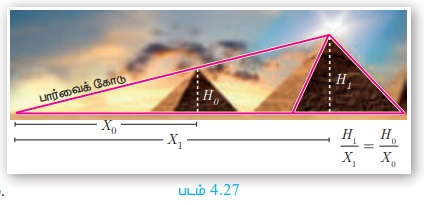
தேல்ஸ் தேற்றத்தின் கண்டுபிடிப்பே ஒரு ஆர்வத்தைத் தூண்டக்கூடிய நிகழ்வாகும். இவர் ஒருமுறை எகிப்திய நாட்டிற்குச் சென்றபோது எகிப்தியர்கள் உருவாக்கிய பல அற்புதப் பிரமிடுகளின் உயரத்தைக் கணக்கிடுமாறு சவால் விடுத்தனர். சவாலை ஏற்றுக்கொண்ட தேல்ஸ், வடிவொத்த முக்கோணக் கருத்துகளைப் பயன்படுத்திச் சவாலில் வெற்றி பெற்றார். படத்தில் X0, X1 மற்றும் H0 ஆகியவற்றின் மதிப்புகள் தெரியும். எனில், பிரமிடின் உயரம் H1 - ஐக் கணக்கிடலாம். இது வடிவியலின் மற்றொரு வெற்றிகரமான பயன்பாடாகும்.

அடிப்படை விகிதச்சமத் தேற்றம் அல்லது தேல்ஸ் தேற்றத்தைப் புரிந்து கொள்வதற்குக் கீழ்க்கண்ட செயல்பாட்டை அறிவோம்.

செயல்பாடு 2 

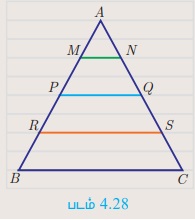
முக்கோணம் ABC-யின் அடிப்பக்கமானது கோடிட்ட காகிதத்தின் ஒரு கோட்டின் மேல் அமையுமாறு எடுத்துக் கொள்க. பல இணை கோடுகள் முக்கோணம் ABC-யை வெட்டும். இந்த இணைகோடுகளில் ஏதேனும் ஓர் இணைக்கோட்டை எடுத்துக்கொள்க. மேலும் இக்கோடு பக்கங்கள் AB மற்றும் AC-ஐ முறையே P மற்றும் Q-யில் வெட்டுகிறது என்க. 

AP /PB மற்றும் AQ /QC -யின் விகிதங்களைக் காணமுடியுமா? AP, PB, AQ மற்றும் QC-ஐ அளவுகோலைக் கொண்டு அளவிட்டு விகிதங்கள் சமமாக உள்ளதா என்பதைச் சரிபார்க்கவும். வெவ்வேறு இணைகோடுகள் MN, RS-க்கு AM/MB, AN/NC மற்றும் AR/RB, AS/SC ஆகிய விகிதங்களைக் காண்க. இவ்விகிதங்கள் சமமாக உள்ளதா? இந்த முடிவுகளில் இருந்து வடிவியலின் மிக முக்கியமான தேற்றத்தைப் பற்றி நாம் விவாதிப்போம்.

தேற்றம் 1: 

அடிப்படை விகிதச்சம தேற்றம் அல்லது தேல்ஸ் தேற்றம் (Basic Proportionality Theorem (BPT) or Thales theorem) 

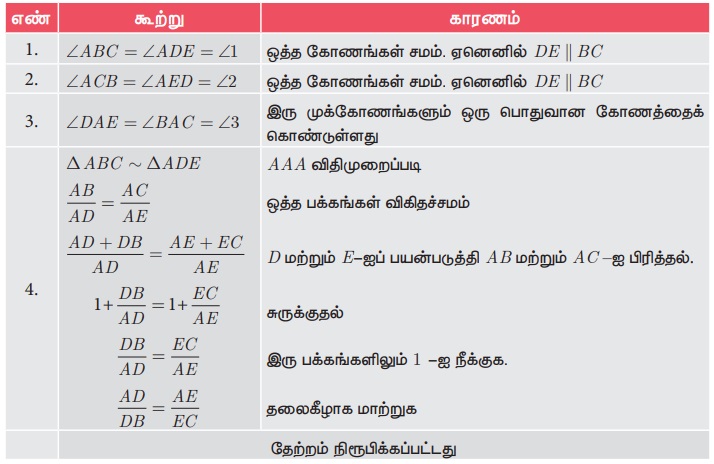
கூற்று

ஒரு நேர்கோடு முக்கோணத்தின் ஒரு பக்கத்திற்கு இணையாகவும் மற்ற இரு பக்கங்களை வெட்டுமாறும் வரையப்பட்டால் அக்கோடு அவ்விரண்டு பக்கங்களையும் சம விகிதத்தில் பிரிக்கிறது. 

நிரூபணம்

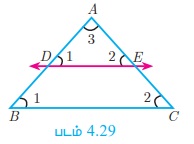
கொடுக்கப்பட்டவை: ΔABC -யில் AB-யின் மேலுள்ள புள்ளி D, AC-யின் மேல் உள்ள புள்ளி E ஆகும். 

நிரூபிக்க: 

AD/DB = AE/EC

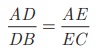
அமைப்பு: 

DE || BC வரைக.

கிளைத்தேற்றம் 

ΔABC -யில் BC-க்கு இணையான நேர்கோடு DE-யானது, AB-ஐ D-யிலும், AC-ஐ E-யிலும் வெட்டினால்

நிரூபணம்: 

ΔABC –யில் DE || BC. 

எனவே, 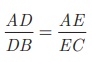AD/DB = AE/EC (அடிப்படை விகிதச்சம தேற்றப்படி) 

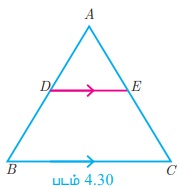
அடிப்படை விகிதசம தேற்றத்தின் மறுதலையும் உண்மையா? பின்வரும் விளக்கத்தின் மூலம் ஆராய்வோம்.

விளக்கம்

படம் 4.31-யில் காட்டியுள்ளபடி, உங்கள் குறிப்பேட்டில் XAY என்ற கோணம் வரைந்து, AX என்ற கதிரில் AB1 = B1B2 = B2 B3 = B 3 B4 = B 4 B = 1 செ.மீ என இருக்குமாறு B1 , B2 , B 3 , B4, B என்ற புள்ளிகளைக் குறிக்கவும்.

இதேபோல் கதிர் AY-யில் AC1=C1C2 = C2C3 = C3C4 = C4C = 2 செ.மீ இருக்குமாறு C1, C2 , C3 ,C4 , C என்ற புள்ளிகளைக் குறிக்கவும். B1 C1   மற்றும் BC -ஐ இணைக்கவும்.

இதிலிருந்து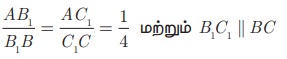

இதே போல் B2C2, B3C3 மற்றும் B4C4 -ஐ இணைப்பதன் மூலம் 

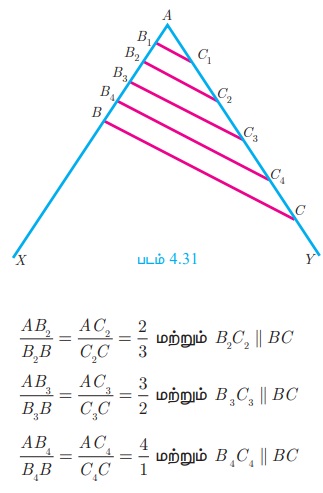
ஆகையால், ஒரு கோடு ஒரு முக்கோணத்தின் இரு பக்கங்களைச் சமவிகிதத்தில் பிரிக்கிறது எனில், அக்கோடு மூன்றாவது பக்கத்திற்கு இணையாகும் என்பதைப் புரிந்து கொள்ளலாம். இக்கருத்தை முறையாக நிரூபிக்கும் தேற்றமானது அடிப்படை விகிதசம தேற்றத்தின் மறுதலையாகும். 

தேற்றம் 2: 

அடிப்படை விகிதசம தேற்றத்தின் மறுதலை (அல்லது) தேல்ஸ் தேற்றத்தின் மறுதலை (Converse of Basic Proportionality Theorem) 

கூற்று

ஒரு நேர்கோடு ஒரு முக்கோணத்தின் இரு பக்கங்களைச் சமவிகிதத்தில் பிரித்தால், அந்நேர்கோடானது மூன்றாவது பக்கத்திற்கு இணையாக இருக்கும். 

நிரூபணம்

கொடுக்கப்பட்டவை: ΔABC -யில்,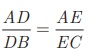

நிரூபிக்க: DE || BC 

அமைப்பு: DE ஆனது BC -க்கு இணையாக

இல்லையெனில், DF || BC என்றவாறு DF -ஐ வரைக.

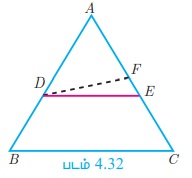
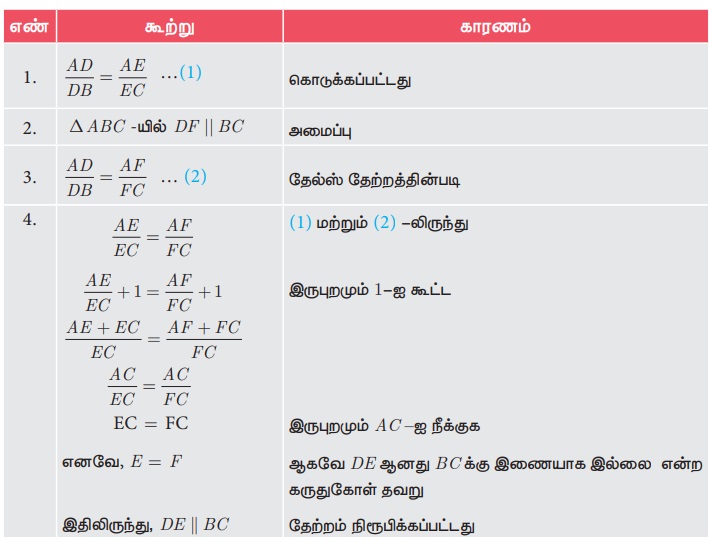
தேற்றம் 3: 

கோண இருசமவெட்டி தேற்றம் (Angle Bisector Theorem) 

கூற்று

ஒரு முக்கோணத்தின் ஒரு கோணத்தின் உட்புற இருசமவெட்டியானது அக்கோணத்தின் எதிர் பக்கத்தை உட்புறமாக அக்கோணத்தினை அடக்கிய பக்கங்களின் விகிதத்தில் பிரிக்கும்.

நிரூபணம்

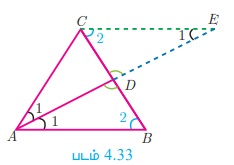
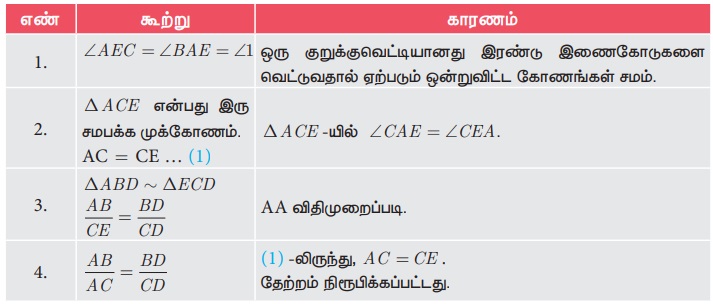
கொடுக்கப்பட்டவை: ΔABC -யில் AD-யானது ∠A -யின் உட்புற இருசமவெட்டி

நிரூபிக்க: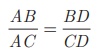

அமைப்பு: AB-க்கு இணையாக C வழியாகச் ஒரு இணைகோடு வரைக. AD-யின் நீட்சியானது C வழியாக செல்லும் கோட்டினை E -யில் சந்திக்கிறது

செயல்பாடு 3

படி 1: படம் 4.34(i)-யில் காட்டியுள்ளபடி, வரைபட அட்டையை முக்கோண வடிவத்தில் வெட்டிக் கொள்ளவும். 

படி 2: புள்ளிகள் C மற்றும் B ஆனது ஒன்றின்மீது ஒன்று பொருந்துமாறு சமச்சீர் கோடு AD-ஐக் கொண்டு மடிக்கவும். 

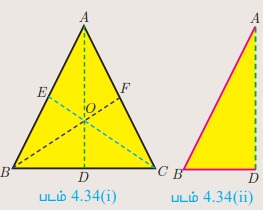
படி 3: இதேபோல CE-ஐ மடிக்கும்போது, புள்ளிகள் B மற்றும் A ஒன்றின்மீது ஒன்று பொருந்தி இருக்கும். 

படி 4: இதேபோல BF -ஐ மடிக்கும்போது, புள்ளிகள் A மற்றும் C ஒன்றின் மீது ஒன்று பொருந்தி இருக்கும் அளவுகோலைப் பயன்படுத்தி AB, AC, BD, DC –யின் மதிப்பைக் காண்க. மேலும், AB/AC, BD/DC ஆனது சமமாக உள்ளதா எனச் சரிபார்க்கவும்? இந்த மூன்று நிலைகளிலிருந்து, ஒரு முக்கோணத்தின் ஒரு கோணத்தின் உட்புற இருசமவெட்டியானது அதன் எதிர் பக்கத்தை உட்புறமாக அக்கோணத்தினை அடக்கிய பக்கங்களின் விகிதத்தில் பிரிக்கிறது. இந்தச் செயல்பாட்டிலிருந்து நீ என்ன முடிவுக்கு வருகிறாய்?

தேற்றம் 4: 

கோண இருசமவெட்டி தேற்றத்தின் மறுதலை (Converse of Angle Bisector Theorem)

கூற்று

ஒரு முக்கோணத்தின் ஒரு முனையிலிருந்து செல்லும் ஒரு நேர்கோடு, அதன் எதிர் பக்கத்தினை உட்புறமாக மற்ற இரு பக்கங்களின் விகிதத்தில் பிரிக்குமானால், அக்கோடு அமைந்த முனைக் கோணத்தினை உட்புறமாக இரு சமமாகப் பிரிக்கும். 

நிரூபணம் 

கொடுக்கப்பட்டது: ABC என்பது ஒரு முக்கோணம். AD ஆனது பக்கம் BC-யை D என்ற புள்ளியில் கோணம் ∠A-யை உள்ளடக்கிய பக்கங்களின் விகிதத்தில் பிரிக்கிறது. 

அதாவது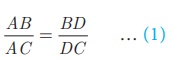

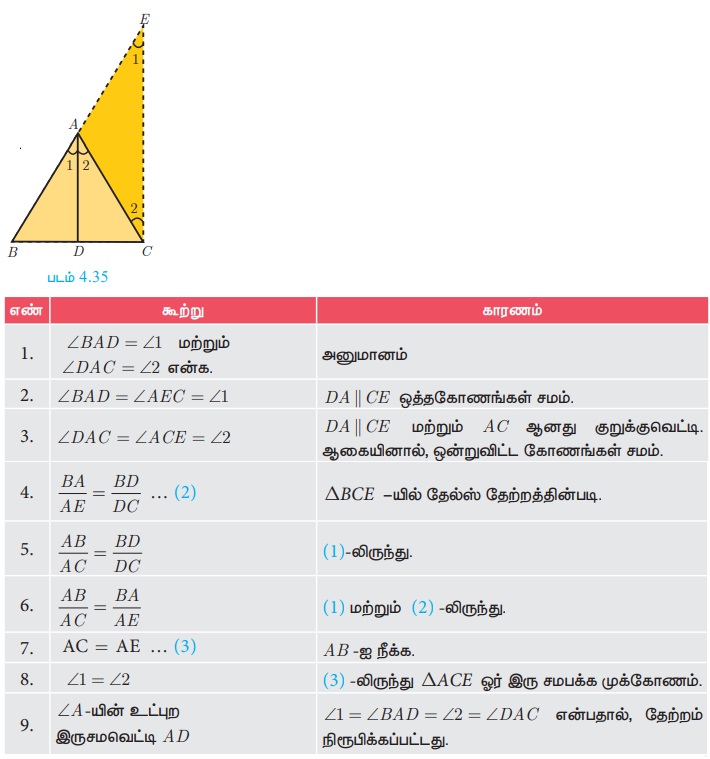
நிரூபிக்க: ∠A-யின் உட்புற இருசமவெட்டி AD. அதாவது ∠1 = ∠2  

அமைப்பு: CE || DA வரைக. BA-யின் நீட்சி E -யில் சந்திக்கிறது. 

எடுத்துக்காட்டு 4.12 

ΔABC -யில் DE || BC, AD = x, DB = x - 2, AE = x + 2 மற்றும் EC = x -1 எனில், பக்கங்கள் AB மற்றும் AC -யின் நீளங்களைக் காண்க.

தீர்வு 

ΔABC -யில் DE || BC.

தேல்ஸ் தேற்றத்தின் மூலம் நாம் பெறுவது,

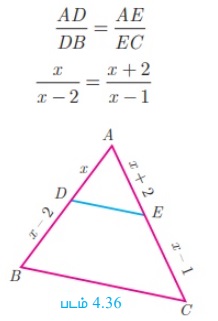
 x/ x-2 = (x + 2)/(x - 1) ⇒ x (x − 1) = (x − 2) (x + 2)

ஆகவே, x 2 − x = x2 – 4 ⇒ x = 4

x = 4, எனில், AD = 4 , DB = x − 2 = 2 , AE = x + 2 = 6 , EC = x – 1 =3

எனவே, AB = AD + DB = 4 + 2 = 6, AC = AE + EC = 6 + 3 = 9.

ஆகவே, AB = 6, AC = 9.

எடுத்துக்காட்டு 4.13 

ΔABC - யின் பக்கங்கள் AB மற்றும் AC-ல் அமைந்த புள்ளிகள் முறையே D மற்றும் E மேலும், AB = 5.6 செ.மீ, AD = 1.4 செ.மீ, A C = 7.2 செ.மீ மற்றும் AE = 1.8 செ.மீ எனில், DE || BC எனக் காட்டுக.

தீர்வு 

AB = 5.6 செ.மீ, AD = 1.4 செ.மீ, AC = 7.2 செ.மீ மற்றும் AE = 1.8 செ.மீ.

BD = AB - AD = 5.6 - 1.4 = 4.2 செ.மீ

மற்றும் EC = AC – AE = 7.2 – 1.8 = 5.4 செ.மீ.

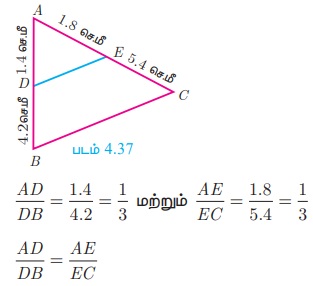
எனவே, அடிப்படை விகிதசம தேற்றத்தின் மறுதலையின்படி DE - யானது BC-க்கு இணை ஆகும்.

எடுத்துக்காட்டு 4.14 

படம் 4.38-யில், DE || AC மற்றும் DC || AP எனில், 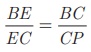என நிறுவுக.

தீர்வு 

ΔBPA, -யில், DC || AP என்பதால், அடிப்படை விகிதசம தேற்றத்தின்படி,

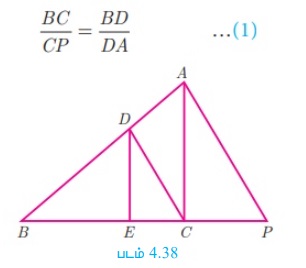
ΔBCA-யில், DE || AC என்பதால், அடிப்படை விகிதசம தேற்றத்தின்படி,

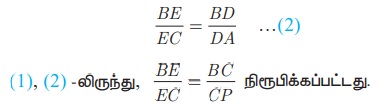
எடுத்துக்காட்டு 4.15 

படம் 4.39 -யில் ∠A -யின் இருசமவெட்டி AD ஆகும். 

BD = 4 செ.மீ, DC = 3 செ.மீ மற்றும் AB = 6 செ.மீ எனில், AC - யைக் காண்க?

தீர்வு 

ΔABC -யில், ∠A-யின் இருசமவெட்டி AD ஆகும். 

எனவே, கோண இருசமவெட்டித் தேற்றத்தின்படி,

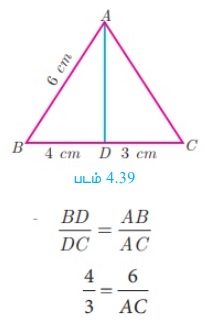
4/3 = 6/ AC ⇒ 4AC = 18. எனவே, AC = 9/2 =4.5 செ.மீ

எடுத்துக்காட்டு 4.16 

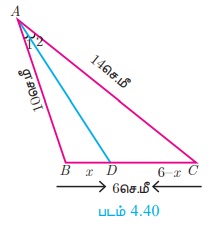
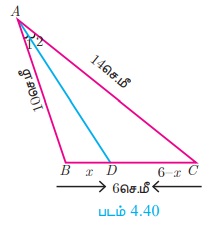
படம் 4.40-யில், AD என்பது ∠BAC -யின் இருசமவெட்டியாகும். 

AB = 10 செ.மீ, AC = 14 செ.மீ மற்றும் BC = 6 செ.மீ. எனில், BD மற்றும் DC-ஐ காண்க. 

தீர்வு 

BD = x செ.மீ என்க. DC = (6 - x)செ.மீ

∠A -யின் இருசமவெட்டி AD ஆகும் 

எனவே, கோண இருசமவெட்டி தேற்றத்தின்படி,

ஆகவே, BD = 2.5 செ.மீ, DC = 6 − x = 6 − 2.5 = 3.5 செ.மீ

முன்னேற்றச் சோதனை

1. முக்கோணத்தின் ஒரு பக்கத்திற்கு ___________ வரையப்படும் நேர்கோடு மற்ற இரு பக்கங்களை விகிதசமத்தில் பிரிக்கும். 

2. அடிப்படை விகிதசம தேற்றம் ______என்றும் அழைக்கப்படுகிறது.

3. ΔABC என்பது சமபக்க முக்கோணம் என்க. இதில் BC-யின் மேலுள்ள புள்ளி D மற்றும் ∠A-யின் உட்புற இருசமவெட்டி AD ஆகும். கோண இருசமவெட்டி தேற்றத்தைப் பயன்படுத்தினால் BD/DC என்பது ____ ஆகும். 

4. ஒரு முக்கோணத்தின் ஒரு கோணத்தின் _____ ஆனது அக்கோணத்தின் எதிர் பக்கத்தை உட்புறமாக அக்கோணத்தினை அடக்கிய பக்கங்களின் விகிதத்தில் பிரிக்கும்.

5. ΔABC -யில் பக்கம் BC-யின் நடுக்கோடு AD-யானது ∠A -யின் இருசமவெட்டியாகவும் இருந்தால், AB/AC ஆனது _____.