பரிமாண பகுப்பாய்வு - இயற்பியல் அளவுகளின் பரிமாணங்கள் | 11th Physics : UNIT 1 : Nature of Physical World and Measurement
11வது இயற்பியல் : அலகு 1 : இயல் உலகத்தின் தன்மையும் அளவீட்டியலும்
இயற்பியல் அளவுகளின் பரிமாணங்கள்
இயற்பியல் அளவுகளின் பரிமாணங்கள்
இயந்திரவியலில் நிறை, காலம், நீளம், திசைவேகம், முடுக்கம் போன்ற பல இயற்பியல் அளவுகளைப் பற்றி நாம் படித்துள்ளோம். இந்த இயற்பியல் அளவுகளின் பரிமாணங்கள் சார்ந்த அடிப்படை அளவுகளின் பரிமாணங்களான M, L மற்றும் T யைப் பயன்படுத்தி எழுதப்படுகிறது. ஒரு இயற்பியல் அளவின் பரிமாணம் பின்வருமாறு வரையறை செய்யப்படுகிறது. ஒரு இயற்பியல் அளவை எழுதப் பயன்படும் சார்பற்ற அடிப்படை அளவுகளின் பரிமாணங்களின் அடுக்குக் குறியீடுகளின் மதிப்பே அந்த இயற்பியல் அளவின் பரிமாணம் ஆகும். இது கீழ்க்கண்டவாறு குறிக்கப்படுகிறது [இயற்பியல் அளவு].

எடுத்துக்காட்டாக, [நீளம்] என்பது நீளத்தின் பரிமாணமாகும், பரப்பு என்பது பரப்பின் பரிமாணத்தைக் குறிக்கும் இது போன்றே மற்றவற்றையும் குறிப்பிடலாம். அடிப்படை அளவுகளைப்பயன்படுத்தி நீளத்தின் பரிமாணத்தை பின்வருமாறு குறிப்பிடலாம்.
நீளம்] = M° LT° = L
இதேபோன்று, [பரப்பு] = M° L2 T° = L2
இவ்வாறே [பருமன்] = M° L3 T° = L3
இங்கு குறிப்பிட்டுள்ள அனைத்து உதாரணங்களிலும் அடிப்படை அளவு L ஒன்றுதான். ஆனால் அதன் அடுக்கு வெவ்வேறானவை. அதாவது பரிமாணங்கள் வெவ்வேறானவை. எண் மட்டுமே உள்ள அளவிற்கு அடிப்படை அளவின் அடுக்கு சுழியாகும்.
⇒ [2]=M° L° T° (பரிமாணமற்றது)
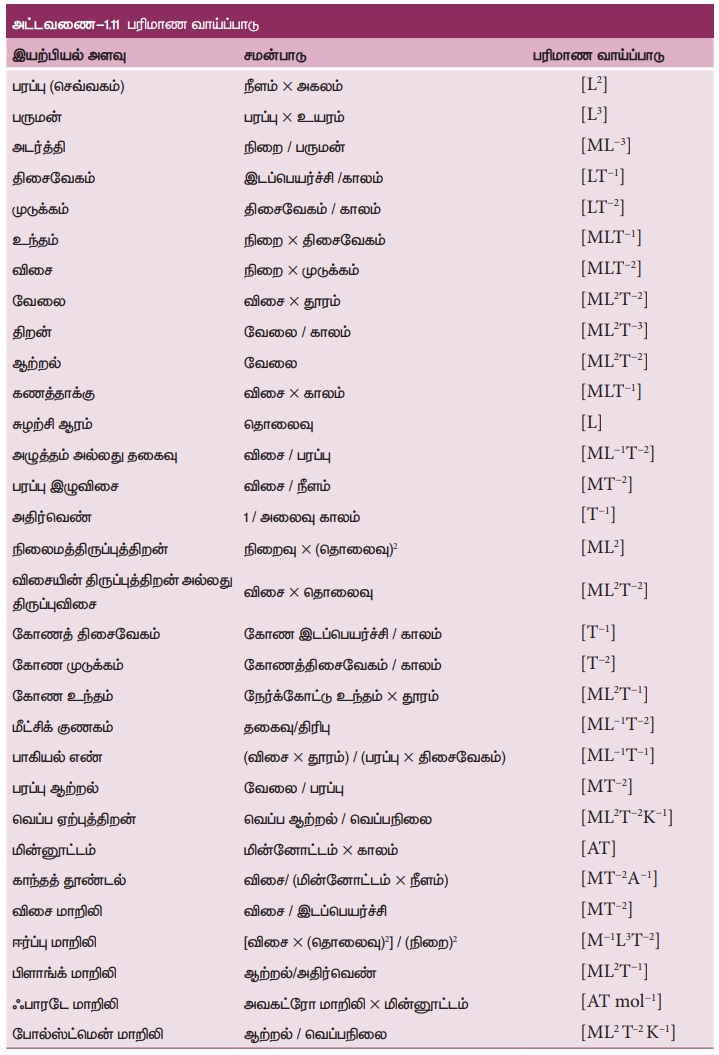
மேலும் சில இயற்பியல் அளவுகளின் பரிமாணத்தை இங்கு காணலாம்.

வேகம் என்பது ஸ்கேலர் அளவு மற்றும் திசைவேகம் என்பது வெக்டர் அளவு என்பதை இங்கு நினைவு கூறவும். (ஸ்கேலர் மற்றும் வெக்டர் போன்றவற்றைப்பற்றி அலகு 2 - இல் படிக்கலாம்) ஆனால் இவ்விரண்டின் பரிமாண வாய்ப்பாடும். ஒன்றே

ஓரலகு நேரத்திற்கான திசைவேகம், முடுக்கமாகும். நேர்க்கோட்டு உந்தம் அல்லது உந்தம்,
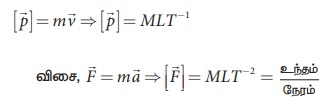
இந்த சமன்பாடு எல்லாவிதமான விசைக்கும் பொருந்தும். இயற்கையில் நான்கு வகையான விசைகளே நீக்கமற நிறைந்துள்ளன அவை, வலிமையான விசை, மின்காந்த விசை, வலிமை குறைந்த விசை மற்றும் ஈர்ப்பு விசை ஆகும்.
மேலும் உராய்வுவிசை, மைய நோக்குவிசை, மையவிலக்குவிசை போன்ற அனைத்து விசைகளுக்கும் பரிமாண வாய்ப்பாடு MLT-2 ஆகும்.
கணத்தாக்கு, 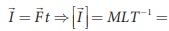 உந்தத்தின் பரிமாணம்
உந்தத்தின் பரிமாணம்
நேர்க்கோட்டு உந்தத்தின் திருப்புத்திறன் கோண உந்தமாகும் (அலகு 5 இல் விவரிக்கப்பட்டுள்ளது),
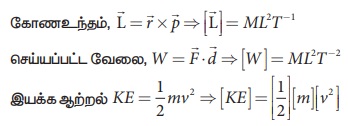
இங்கு, 1/2 என்பது பரிமாணமற்ற ஓர் எண்ணாகும். எனவே இயக்க ஆற்றலின் பரிமாணவாய்ப்பாடு [KE] =[m] [v2] = ML2T−2 இதேபோன்று நிலையாற்றலின் பரிமாணவாய்ப்பாட்டை பின்வருமாறு கண்டறியலாம்.
எடுத்துக்காட்டாக ஈர்ப்பழுத்த ஆற்றலைக் கருதுக
[PE] =[m] [g] [h] = ML2T−2 இங்கு m என்பது பொருளின் நிறையாகும், g என்பது புவிஈர்ப்பு முடுக்கமாகும். மேலும் h என்பது புவிப்பரப்பிலிருந்து பொருளின் உயரமாகும். எனவே [PE] =[m] [g] [h] = ML2T−2. எந்தவகையான ஆற்றலாக இருப்பினும் (அக ஆற்றல், மொத்த ஆற்றல் மற்றும் மேலும் பல வகையான ஆற்றல்கள்) அதன் பரிமாணம்
[ஆற்றல்] = ML2T−2
விசையின் திருப்புத்திறன், திருப்புவிசை என அழைக்கப்படும், 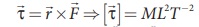 (τ என்ற கிரேக்க உயிரெழுத்தை "ட்டவ்" என வாசிக்கவும்) திருப்புவிசை மற்றும் ஆற்றல் இவ்விரண்டின் பரிமாணமும் ஒன்றே. ஆனால் அவை வெவ்வேறான இயற்பியல் அளவுகளாகும். மேலும் இவ்விரண்டு அளவுகளில் ஒன்று (ஆற்றல்) ஸ்கேலர் அளவாகும் மற்றொன்று (திருப்புவிசை) வெக்டர் அளவாகும். இயற்பியல் அளவுகள் ஒரே பரிமாண வாய்ப்பாடு பெற்றிருந்தாலும் அவை ஒரே இயற்பியல் அளவாக இருக்க வேண்டிய அவசியமில்லை.
(τ என்ற கிரேக்க உயிரெழுத்தை "ட்டவ்" என வாசிக்கவும்) திருப்புவிசை மற்றும் ஆற்றல் இவ்விரண்டின் பரிமாணமும் ஒன்றே. ஆனால் அவை வெவ்வேறான இயற்பியல் அளவுகளாகும். மேலும் இவ்விரண்டு அளவுகளில் ஒன்று (ஆற்றல்) ஸ்கேலர் அளவாகும் மற்றொன்று (திருப்புவிசை) வெக்டர் அளவாகும். இயற்பியல் அளவுகள் ஒரே பரிமாண வாய்ப்பாடு பெற்றிருந்தாலும் அவை ஒரே இயற்பியல் அளவாக இருக்க வேண்டிய அவசியமில்லை.