பரிமாணங்களின் பகுப்பாய்வு

பரிமாணங்களின் பகுப்பாய்வு

இயற்பியல் அளவுகளின் பரிமாணங்கள்

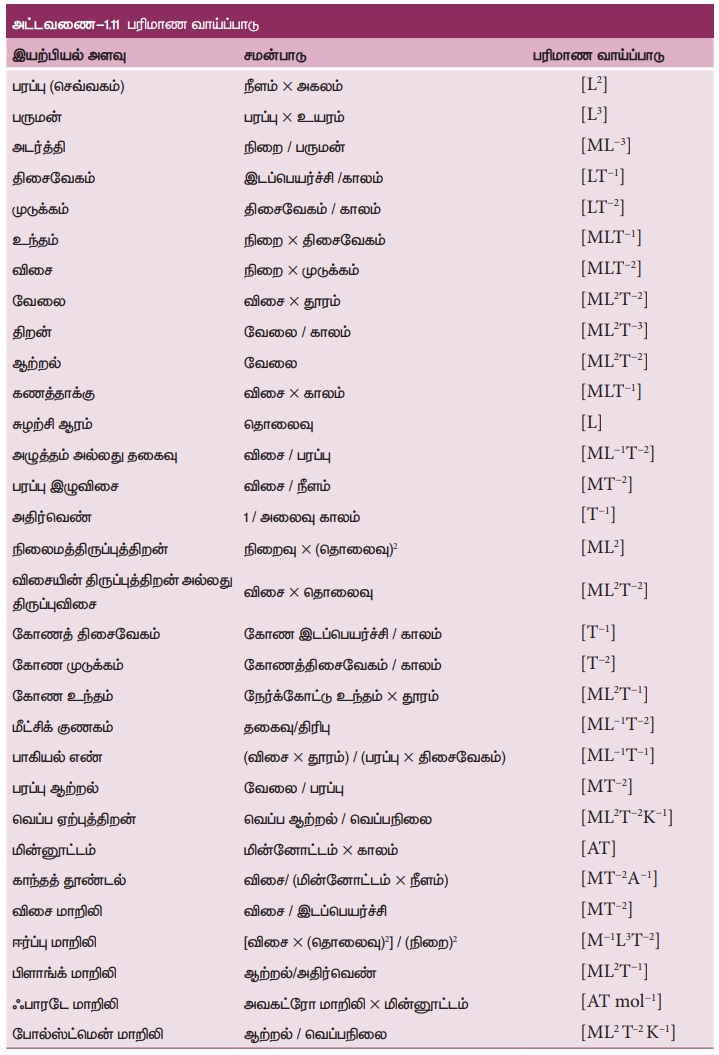
இயந்திரவியலில் நிறை, காலம், நீளம், திசைவேகம், முடுக்கம் போன்ற பல இயற்பியல் அளவுகளைப் பற்றி நாம் படித்துள்ளோம். இந்த இயற்பியல் அளவுகளின் பரிமாணங்கள் சார்ந்த அடிப்படை அளவுகளின் பரிமாணங்களான M, L மற்றும் T யைப் பயன்படுத்தி எழுதப்படுகிறது. ஒரு இயற்பியல் அளவின் பரிமாணம் பின்வருமாறு வரையறை செய்யப்படுகிறது. ஒரு இயற்பியல் அளவை எழுதப் பயன்படும் சார்பற்ற அடிப்படை அளவுகளின் பரிமாணங்களின் அடுக்குக் குறியீடுகளின் மதிப்பே அந்த இயற்பியல் அளவின் பரிமாணம் ஆகும். இது கீழ்க்கண்டவாறு குறிக்கப்படுகிறது [இயற்பியல் அளவு].

எடுத்துக்காட்டாக, [நீளம்] என்பது நீளத்தின் பரிமாணமாகும், பரப்பு என்பது பரப்பின் பரிமாணத்தைக் குறிக்கும் இது போன்றே மற்றவற்றையும் குறிப்பிடலாம். அடிப்படை அளவுகளைப்பயன்படுத்தி நீளத்தின் பரிமாணத்தை பின்வருமாறு குறிப்பிடலாம்.

நீளம்] = M° LT° = L 

இதேபோன்று, [பரப்பு] = M° L2 T° = L2 

இவ்வாறே [பருமன்] = M° L3 T° = L3

இங்கு குறிப்பிட்டுள்ள அனைத்து உதாரணங்களிலும் அடிப்படை அளவு L ஒன்றுதான். ஆனால் அதன் அடுக்கு வெவ்வேறானவை. அதாவது பரிமாணங்கள் வெவ்வேறானவை. எண் மட்டுமே உள்ள அளவிற்கு அடிப்படை அளவின் அடுக்கு சுழியாகும்.

⇒ [2]=M° L° T° (பரிமாணமற்றது) 

மேலும் சில இயற்பியல் அளவுகளின் பரிமாணத்தை இங்கு காணலாம்.

வேகம் என்பது ஸ்கேலர் அளவு மற்றும் திசைவேகம் என்பது வெக்டர் அளவு என்பதை இங்கு நினைவு கூறவும். (ஸ்கேலர் மற்றும் வெக்டர் போன்றவற்றைப்பற்றி அலகு 2 - இல் படிக்கலாம்) ஆனால் இவ்விரண்டின் பரிமாண வாய்ப்பாடும். ஒன்றே

ஓரலகு நேரத்திற்கான திசைவேகம், முடுக்கமாகும். நேர்க்கோட்டு உந்தம் அல்லது உந்தம்,

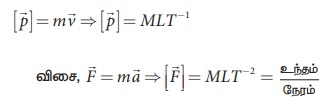
இந்த சமன்பாடு எல்லாவிதமான விசைக்கும் பொருந்தும். இயற்கையில் நான்கு வகையான விசைகளே நீக்கமற நிறைந்துள்ளன அவை, வலிமையான விசை, மின்காந்த விசை, வலிமை குறைந்த விசை மற்றும் ஈர்ப்பு விசை ஆகும். 

மேலும் உராய்வுவிசை, மைய நோக்குவிசை, மையவிலக்குவிசை போன்ற அனைத்து விசைகளுக்கும் பரிமாண வாய்ப்பாடு MLT-2 ஆகும்.

கணத்தாக்கு, 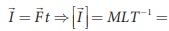உந்தத்தின் பரிமாணம்

நேர்க்கோட்டு உந்தத்தின் திருப்புத்திறன் கோண உந்தமாகும் (அலகு 5 இல் விவரிக்கப்பட்டுள்ளது), 

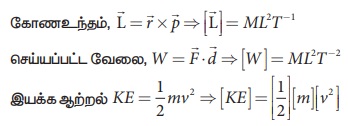
இங்கு, 1/2 என்பது பரிமாணமற்ற ஓர் எண்ணாகும். எனவே இயக்க ஆற்றலின் பரிமாணவாய்ப்பாடு [KE] =[m] [v2] = ML2T−2 இதேபோன்று நிலையாற்றலின் பரிமாணவாய்ப்பாட்டை பின்வருமாறு கண்டறியலாம். 

எடுத்துக்காட்டாக ஈர்ப்பழுத்த ஆற்றலைக் கருதுக 

[PE] =[m] [g] [h] = ML2T−2 இங்கு m என்பது பொருளின் நிறையாகும், g என்பது புவிஈர்ப்பு முடுக்கமாகும். மேலும் h என்பது புவிப்பரப்பிலிருந்து பொருளின் உயரமாகும். எனவே [PE] =[m] [g] [h] = ML2T−2.  எந்தவகையான ஆற்றலாக இருப்பினும் (அக ஆற்றல், மொத்த ஆற்றல் மற்றும் மேலும் பல வகையான ஆற்றல்கள்) அதன் பரிமாணம்

[ஆற்றல்] = ML2T−2

விசையின் திருப்புத்திறன், திருப்புவிசை என அழைக்கப்படும், 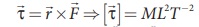(τ என்ற கிரேக்க உயிரெழுத்தை "ட்டவ்" என வாசிக்கவும்) திருப்புவிசை மற்றும் ஆற்றல் இவ்விரண்டின் பரிமாணமும் ஒன்றே. ஆனால் அவை வெவ்வேறான இயற்பியல் அளவுகளாகும். மேலும் இவ்விரண்டு அளவுகளில் ஒன்று (ஆற்றல்) ஸ்கேலர் அளவாகும் மற்றொன்று (திருப்புவிசை) வெக்டர் அளவாகும். இயற்பியல் அளவுகள் ஒரே பரிமாண வாய்ப்பாடு பெற்றிருந்தாலும் அவை ஒரே இயற்பியல் அளவாக இருக்க வேண்டிய அவசியமில்லை.

1. இயற்பியலில் நாம் வெவ்வேறு இடங்களில் பரிமாணம் என்ற சொல்லை பயன்படுத்துகிறோம். எனவே அடிக்கடி நமக்கு பரிமாணம் என்பதைப்பற்றி ஐயம் ஏற்படும். உதாரணமாக ஆற்றலின்பரிமாணம், ஒரு பரிமாண இயக்கம் மற்றும் அணுஒன்றின் பரிமாணம் போன்ற சொற்றொடர்களைப் பயன்படுத்துவோம். இயற்பியல் அளவு ஒன்றின் பரிமாணம் என்பது அதனை விவரிக்கும் அடிப்படை அளவின் அடுக்குறியே பரிமாணமே என்பதை நினைவில் கொள்ளவேண்டும். ஒரு பரிமாண இயக்கம், இருபரிமாண இயக்கம் மற்றும் முப்பரிமாண இயக்கம் போன்றவை அந்த பொருள் இயங்கும் வெளியின் (space) பரிமாணத்தைக் குறிக்கின்றன. அணுவின் பரிமாணம் என்பது அணுவின் அளவைக் குறிக்கின்றது. எனவே வெறுமனே பரிமாணம் என்பது அர்த்தமற்றதாகும். இடத்திற்கு ஏற்ப பரிமாணம் என்பதன் பொருளை புரிந்து கொள்ள வேண்டும்.

2.sinθ, cosθ போன்ற அனைத்து முக்கோணவியல் சார்புகளும் பரிமாணமற்றவைகளாகும் (θ பரிமாணமற்றது), அடுக்குக்குறி சார்புகள் ex மற்றும் மடக்கை சார்புகள் lnx போன்றவைகளும் பரிமாணமற்றவைகளாகும் (x க்கு பரிமாணம் இருக்கக்கூடாது) தொடர்

விரிவாக்கம் (முடிவுறு அல்லது முடிவற்ற) செய்யப்பட்ட சார்பின் விரிவில் xo, x1, x2 , .... என்ற உறுப்புகள் காணப்பட்டால் x என்பது நிச்சயமாக பரிமாணமற்ற அளவாகும்.

பரிமாணமுள்ள அளவுகள், பரிமாணமற்ற அளவுகள், பரிமாணத்தின் ஒருபடித்தான நெறிமுறை

பரிமாணங்களைப் பொறுத்து, இயற்பியல் அளவுகளை நான்கு வகைகளாக வகைப்படுத்த முடியும்.

(1) பரிமாணமுள்ள மாறிகள்

எந்த ஓர் இயற்பியல் அளவு பரிமாணத்தையும் மாறுபட்ட மதிப்புகளையும் பெற்றுள்ளதோ அவை பரிமாணமுள்ள மாறிகள் என அழைக்கப்படுகின்றன.

எ.கா:- பரப்பு, கன அளவு, திசைவேகம் மற்றும் பல.

(2) பரிமாணமற்ற மாறிகள்

எந்த இயற்பியல் அளவுகள் பரிமாணம் அற்று ஆனால் மாறுபட்ட மதிப்புகளைக் கொண்டுள்ளதோ அவை பரிமாணமற்ற மாறிகள் என அழைக்கப்படுகின்றன.

எ.கா:- ஒப்படர்த்தி, திரிபு, ஒளிவிலகல் எண் மற்றும் பல.

(3) பரிமாணமுள்ள மாறிலிகள்

எந்த இயற்பியல் அளவுகள் பரிமாணத்துடன் நிலையான மதிப்பைப் பெற்றுள்ளதோ அவை பரிமாணமுள்ள மாறிலிகள் என அழைக்கப்படுகிறது. எ.கா:- ஈர்ப்பியல் மாறிலி, பிளாங் மாறிலி மற்றும் பல.

(4) பரிமாணமற்ற மாறிலிகள் 

ஒரு மாறிலி பரிமாணமற்று இருப்பின் அவை பரிமாணமற்ற மாறிலிகள் எனப்படுகின்றன. எ.கா:T, e (ஆய்லர் எண்) எண்கள் மற்றும் பல.

பரிமாணங்களின் ஒருபடித்தான நெறிமுறை

பரிமாணங்களின் ஒருப்படித்தான நெறிமுறைப்படி ஒரு சமன்பாட்டில் உள்ள ஒவ்வொரு உறுப்பின் பரிமாணங்களும் சமமாகும். எடுத்துக்காட்டாக, v2 = u2 + 2as என்ற சமன்பாட்டில் v2, u2 மற்றும் 2as ஆகியவற்றின் பரிமாணங்கள் ஒத்ததாகவும் [L2T-2] க்கு சமமாகவும் இருக்கும்.

பரிமாணப்பகுப்பாய்வின் பயன்பாடுகளும் வரம்புகளும் 

இம்முறையானது, 

(i) இயற்பியல் அளவு ஒன்றை ஒரு அலகிடும் முறையிலிருந்து மற்றொரு அலகிடும் முறைக்கு மாற்றப் பயன்படுகிறது. 

(ii) கொடுக்கப்பட்ட சமன்பாடு பரிமாண முறைப்படி சரியானதா என சோதிக்கப் பயன்படுகிறது. 

(iii) வெவ்வேறு இயற்பியல் அளவுகளுக்கிடையே உள்ள தொடர்பினைப் பெற பயன்படுகிறது. 

(i) இயற்பியல் அளவு ஒன்றை ஒரு அலகிடும் முறையில் இருந்து மற்றொரு அலகிடும் முறைக்கு மாற்றுதல் 

இந்த முறையானது ஓர் அளவின் எண் மதிப்பையும் (n) அதன் அலகையும் (u) பெருக்கக் கிடைப்பது ஒரு மாறிலி என்ற தத்துவத்தின் அடிப்படையிலானது.

அதாவது n[u] = மாறிலி

அல்லது n1[u1] = n2[u2] 

ஓர் இயற்பியல் அளவானது நிறையின் 'a' பரிமாணத்தையும், நீளத்தின் ‘b’ பரிமாணத்தினையும், காலத்தின் பரிமாணத்தையும் பெற்றுள்ளதாக கொள்வோம். 

ஓர் அலகிடும் முறையின் அடிப்படை அலகுகள். M1,L1 மற்றும் T1 எனவும் மற்றொரு அலகிடும் முறையின் அடிப்படை அலகுகள் முறையே M2, L2, மற்றும் T2, எனவும் கொண்டால்,

n1 [M1a L1b T1c] = n2 [M2a L2b T2c]

இதிலிருந்து ஒரு இயற்பியல் அளவின் எண் மதிப்பினை ஓர் அலகிடும் முறையில் இருந்து மற்றொரு முறைக்கு மாற்ற முடியும்.

(ii) பரிமாண முறையில் கொடுக்கப்பட்ட இயற்பியல் சமன்பாட்டை சரியா என சோதித்தல் 

v = u + at என்ற இயக்கச் சமன்பாட்டை எடுத்துக்கொள்வோம்.

[LT−1] = [LT−1] + [LT−2] [T]

[LT−1] = [LT−1] + [LT−1]

(ஒரே மாதிரியான பரிமாணங்களை பெற்றுள்ள அளவுகளையே கூட்ட முடியும்) 

இருபுறமும் உள்ள பரிமாணங்கள் சமம் என்பதை நாம் காண்கிறோம். எனவே இந்த சமன்பாடு பரிமாண முறையில் சரியானது.

(iii) வெவ்வேறு இயற்பியல் அளவுகளுக்கிடையே உள்ள தொடர்பினைத் தரும் சமன்பாட்டினைப் பெறுதல் 

Q என்ற இயற்பியல் அளவு Q1, Q2, மற்றும் Q3, ஆகியவற்றைப் பொறுத்தது எனில்

Q α Q1a Q2b Q3c

Q = k Q1a Q2b Q3c

இங்கு k - பரிமாணமற்ற மாறிலி. Q, Q1, Q2 மற்றும் Q3, ஆகியவற்றின் பரிமாண வாய்ப்பாட்டை பிரதியிட்டு, பரிமாணத்தின் ஒரு படித்தான நெறிமுறைப்படி M, L, T அடுக்குகள் இருபுறமும் சமன்படுத்தப்படுகிறது. 

இதன் மூலம் a, b, c - இன் மதிப்புகளைப் பெற்று சமன்பாட்டைப் பெறலாம்.

பரிமாண பகுப்பாய்வின் வரம்புகள் 

1. எண்கள், π, e (ஆய்லர் எண்) போன்ற பரிமாணமற்ற மாறிலிகளின் மதிப்பை இம்முறையின் மூலம் பெற முடியாது. 

2. கொடுக்கப்பட்டுள்ள அளவு வெக்டர் அளவா? அல்லது ஸ்கேலர் அளவா? என்பதை இம்முறை மூலம் தீர்மானிக்க முடியாது. 

3. திரிகோணமிதி, அடுக்குக்குறி மற்றும் மடக்கை சார்புகள் உள்ளடங்கிய சமன்பாடுகளின் தொடர்புகளைக் கண்டறிய இம்முறையில் இயலாது. 

4. மூன்றுக்கு மேற்பட்ட இயற்பியல் அளவுகள் உள்ளடங்கிய சமன்பாடுகளுக்கு இம்முறையைப் பயன்படுத்த இயலாது.

5. இம்முறையில் ஒரு சமன்பாடு பரிமாணமுறையில் சரியானதா, என்றே மெய்ப்பிக்க முடியும் அதன் உண்மையான சமன்பாட்டைக் கண்டறிய முடியாது.

எடுத்துக்காட்டாக, S = ut + 1/3 at2 என்பது பரிமாண முறைப்படி சரி. ஆனால் உண்மையான சமன்பாடு S = ut +1/2 at2 ஆகும்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்

(i) இயற்பியல் அளவு ஒன்றை ஒரு அலகிடும் முறையில் இருந்து மற்றொரு அலகிடும் முறைக்கு மாற்றுதல் 

எடுத்துக்காட்டு 1.12

பரிமாணங்கள் முறையில் 76 cm பாதரச் அழுத்தத்தை Nm-2 என்ற அலகிற்கு மாற்றுக.

தீர்வு 

CGS முறையில் 76 cm பாதரச அழுத்தம் (P1) = 76 × 13.6 × 980 dyne cm-2

SI முறையில் P-ன் மதிப்பு (P2)=?

எடுத்துக்காட்டு: 1.13

SI முறையில் ஈர்ப்பியல் மாறிலியின் மதிப்பு GSI = 6.6 × 10-11Nm2kg-2, எனில் CGS முறையில் அதன் மதிப்பைக் கணக்கிடுக? 

தீர்வு 

SI முறையில் ஈர்ப்பு மாறிலி GSI எனவும் cgs முறையில் Gcgs எனவும் கொள்க.

(ii) பரிமாண முறையில் கொடுக்கப்பட்ட இயற்பியல் சமன்பாட்டை சரியா என சோதித்தல் 

எடுத்துக்காட்டு: 1.14

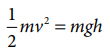என்ற சமன்பாட்டை பரிமாணப் பகுப்பாய்வு முறைப்படி சரியானதா என கண்டறிக.

தீர்வு

இருபுறங்களிலும் பரிமாணங்கள் சமம். எனவே 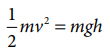என்ற சமன்பாடு பரிமாண முறைப்படி சரி.

(iii) வெவ்வேறு இயற்பியல் அளவுகளுக்கிடையே உள்ள தொடர்பினைத் தரும் சமன்பாட்டினைப் பெறுதல் 

எடுத்துக்காட்டு: 1.15 

தனிஊசலின் அலைவு நேரத்திற்கான கோவையை பரிமாண முறையில் பெறுக. அலைவு நேரமானது. (i) ஊசல் குண்டின் நிறை 'm'(ii) ஊசலின் நீளம் ‘l’' (ii) அவ்விடத்தில் புவியீர்ப்பு முடுக்கம் g ஆகியவற்றைச் சார்ந்தது. (மாறிலி k = 2π) 

தீர்வு

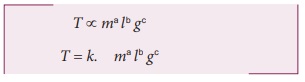
k என்பது பரிமாணமற்ற மாறிலி. மேற்கண்ட சமன்பாட்டில் பரிமாணங்களை பிரதியிட்ட

சமன்பாட்டின் இருபுறமும் உள்ள M, L T-ன் படிகளை சமன் செய்ய

a = 0, b + c = 0, -2c = 1 

சமன்பாடுகளைத் தீர்க்க

a = 0, b = 1/2, மற்றும் c = -1/2 

a,b மற்றும் c மதிப்புகளை சமன்பாடு 1 இல் பிரதியிட T = k. m0  l1/2 g−1/2