பிழைகளின் பரவுதல்

பிழைகளின் பரவுதல்

ஒரு சோதனையில் அதிக அளவுகள் அளக்கப்பட்டு இறுதிக் கணக்கீட்டில் பயன்படுத்தப்படலாம். வெவ்வேறு வகையான கருவிகளைப் பயன்படுத்தி அளவிடலாம். எனவே அளவிடும்போது ஏற்படும் வெவ்வேறு வகையான பிழைகளை மொத்தமாகக் கருத்தில் கொள்ள வேண்டும். 

பிழைகளின் இறுதி முடிவுகள் கீழ்கண்டவற்றைச் சார்ந்துள்ளது. 

i. தனித்தனியான அளவீடுகளில் உள்ள பிழைகள்

ii. கணித செயலிகளின் செயற்பாட்டின் இயல்பைச் சார்ந்து இறுதி முடிவு பெறப்படும். எனவே பிழைகளை ஒன்று சேர்க்கத் தேவையான விதிகளை அறிந்திருக்க வேண்டும். 

வேறுபட்ட கணித செயலிகளின் காரணமாக ஏற்படக்கூடிய பிழைகளின் பெருக்கம் அல்லது பிழைகளின் ஒன்றிணைப்பு ஆகியவற்றின் வெவ்வேறு சாத்தியக் கூறுகளைக் கீழ்க்கண்டவாறு விவாதிக்கலாம்.

(i) இரு அளவுகளின் கூடுதலில் ஏற்படும் பிழைகள் 

ΔA மற்றும் ΔB என்பன முறையே A, B என்ற அளவுகளின் தனிப் பிழைகள் என்க 

A யின் அளவிடப்பட்ட மதிப்பு = A ± ∆A 

B யின் அளவிடப்பட்ட மதிப்பு = B ± ∆B

கூடுதல், Z = A + B 

கூடுதல் Zன் பிழை ΔZ ஆகும்

(ii) இரு அளவுகளின் வேறுபாட்டினால் உருவாகும் பிழைகள்

ΔA மற்றும் ΔB என்பன முறையே A மற்றும் B என்ற அளவுகளின் தனிப் பிழைகள் என்க 

A -ன் அளவிடப்பட்ட மதிப்பு = A ± ΔA

B -ன் அளவிடப்பட்ட மதிப்பு = B ± ΔB

வேறுபாடு, Z = A - B 

வேறுபாடு Zன் பிழை ΔZ ஆகும்

இரு அளவுகளின் வேறுபாட்டினால் ஏற்படும் பிழையின் பெரும மதிப்பானது தனித் தனி அளவுகளின் தனிப் பிழைகளின் கூடுதலுக்குச் சமம்.

(iii) இரு அளவுகளைப் பெருக்குவதால் ஏற்படும் பிழைகள்: 

ΔA மற்றும் ΔB என்பன முறையே A, B என்ற அளவுகளின் தனிப் பிழைகள் என்க 

அவற்றின் பெருக்கல் பலன் Z = AB

Z இன் பிழை ΔZ ஆகும்

Z ± ΔZ = (A ± ΔA) (B ± ΔB)

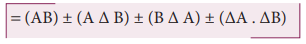
இடது புறத்தை Z ஆலும் வலது புறத்தை AB யிலும் வகுக்க நாம் பெறுவது,

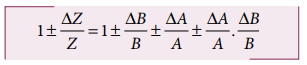
ΔA /A, ΔB / B ஆகியவை மிகக் குறைந்த அளவு எனவே அவற்றின் பெருக்கல் ΔA/A . ΔB/B புறக்கணிக்கப்படுகிறது. Z இன் பெரும் பின்னப் பிழை

இதற்கான மாற்றுமுறை பின் இணைப்பு 2 (A 1.2) இல் கொடுக்கப்பட்டுள்ளது.

(iv) இரு அளவுகளை வகுப்பதால் ஏற்படும் பிழைகள் 

ΔA மற்றும் ΔB என்பன முறையே A, B என்ற அளவுகளின் தனிப் பிழைகள் என்க அவற்றின் பின்னம், Z = A/B

Z இன் பிழை ΔZ ஆகும்

இரு அளவுகளை வகுப்பதால் பெறப்படும் பெரும பின்னப் பிழையானது தனித்தனி அளவுகளின் பின்னப்பிழைகளின் கூடுதலுக்குச் சமம்

(v) அளவின் அடுக்கினால் ஏற்படும் பிழை

A யின் வது அடுக்கு Z என்க Z = An

Zன் பிழை ΔZ எனில்

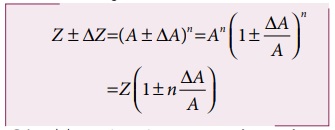
(இங்கு |x|<<1, (1+x)n ≈1+nx, என்ற சமன்பாடு பயன்படுத்தப்படுகிறது). 

இருபுறமும் Z ஆல் வகுக்க

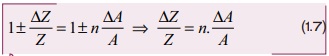
ஒரு அளவின் n ஆவது அடுக்கின் பெரும பின்னப் பிழையானது. அதன் பின்னப்பிழையை n ஆல் பெருக்குதலுக்கு சமம்.

(i) இரு அளவுகளின் கூடுதலில் ஏற்படும் பிழைகள்

எடுத்துக்காட்டு 1.5 

R1 = (100 ± 3) Ω, R2  = (150 ± 2) Ω ஆகிய இரு மின்தடைகள் தொடரிணைப்பில் இணைக்கப்பட்டுள்ளன. அவற்றின் தொகுபயன் மின் தடை என்ன? 

தீர்வு

(ii) இரு அளவுகளின் வேறுபாட்டினால் உருவாகும் பிழைகள்

எடுத்துக்காட்டு 1.6

ஒரு வெப்பநிலைமானி கொண்டு அளவிடப்பட்ட இரு பொருட்களின் வெப்பநிலை t = (20 ± 0.5)°C மற்றும் t = (50 ± 0.5)°C எனில் அவற்றின் வெப்பநிலை வேறுபாட்டையும், பிழையையும் கணக்கிடுக. 

தீர்வு

(iii) இரு அளவுகளைப் பெருக்குவதால் ஏற்படும் பிழைகள்: 

எடுத்துக்காட்டு 1.7

ஒரு செவ்வகத்தின் நீளம் மற்றும் அகலம் முறையே (5.7 ± 0.1) cm மற்றும் (3.4 ± 0.2) cm எனில் செவ்வகத்தின் பரப்பை பிழை எல்லையுடன் கணக்கிடுக. 

தீர்வு 

(iv) இரு அளவுகளை வகுப்பதால் ஏற்படும் பிழைகள் 

எடுத்துக்காட்டு 1.8

ஒரு கம்பிக்கு குறுக்கே உள்ள மின்னழுத்த வேறுபாடு (100 ± 5) V மற்றும் அதன் வழியே பாயும் மின்னோட்டம் (10 ± 0.2) A எனில். அக்கம்பியின் மின்தடையைக் காண்க. 

தீர்வு

(v) அளவின் அடுக்கினால் ஏற்படும் பிழை

எடுத்துக்காட்டு 1.9

ஒரு இயற்பியல் அளவு 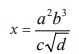என்று கொடுக்கப்பட்டுள்ளது. a, b, c மற்றும் d ஐ அளவிடுதலில் ஏற்படும் விழுக்காட்டுப்பிழைகள் முறையே 4%, 2%, 3% மற்றும் 1% எனில் ன் விழுக்காட்டுப் பிழையைக் காண்க. (NEET 2013) தீர்வு