பயிற்சி 6.1 : முக்கோணவியல்

பயிற்சி 6.1 

1. பின்வரும் முற்றொருமைகளை நிரூபிக்கவும்.

(i) cot θ + tan θ = sec θ cosec θ

(ii) tan4 θ + tan2 θ = sec4 θ − sec2 θ

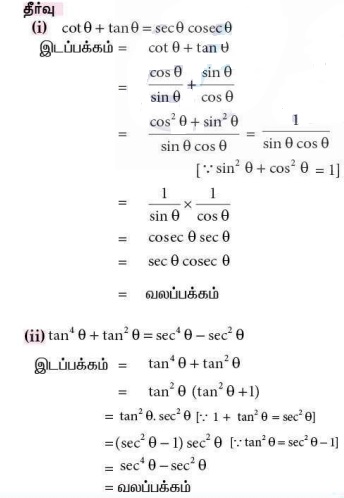
2. பின்வரும் முற்றொருமைகளை நிரூபிக்கவும். 

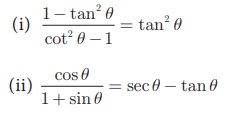
3. பின்வரும் முற்றொருமைகளை நிரூபிக்கவும். 

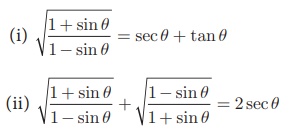
4. பின்வரும் முற்றொருமைகளை நிரூபிக்கவும்.

(i) sec6 θ = tan6 θ + 3 tan2 θ sec2 θ +1

(ii) (sin θ + sec θ)2  + (cos θ + cosec θ)2  = 1 + (sec θ + cosec θ)2

 5. பின்வரும் முற்றொருமைகளை நிரூபிக்கவும்.

(i) sec4 θ (1 − sin4 θ) −2 tan2 θ = 1

(ii)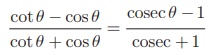 

6. பின்வரும் முற்றொருமைகளை நிரூபிக்கவும்.

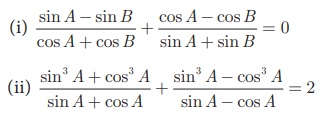
7. (i) sin θ + cos θ = √3, எனில், tan θ + cot θ = 1. என்பதை நிரூபிக்கவும்.

(ii) √3sinθ − cosθ = 0, எனில், tan 3θ = (3 tan θ − tan3θ) / (1 − 3 tan2 θ) - என நிறுவுக.

8. எனக் கொண்டு (m2 + n2) cos2 β = n2 என்பதை நிரூபிக்கவும். 

(ii) cot θ + tan θ = x மற்றும் sec θ − cos θ = y , எனில், (x2y)2/3 – (xy2)2/3 = 1 என்பதை நிரூபிக்கவும். 

9. (i) sin θ + cos θ = p மற்றும் sec θ + cosec θ = q, எனில், q ( p2 − 1) = 2p என்பதை நிரூபிக்கவும்.

(ii) sin θ(1 + sin2 θ) = cos2 θ, எனில், cos6 θ − 4 cos4 θ + 8 cos2 θ = 4 என்பதை நிரூபிக்கவும்.

 10. என்பதை நிரூபிக்கவும்.