முக்கோணவியல் முற்றொருமைகள்

முக்கோணவியல் முற்றொருமைகள் (Trigonometric Identities)

θ -ன் எல்லா மெய்யெண் மதிப்புகளுக்கும் பின்வரும் மூன்று முற்றொருமைகளைப் பெறலாம். 

(i) sin 2 θ + cos2 θ = 1

(ii) 1 + tan2 θ = sec2 θ

(iii) 1 + cot2 θ = cosec2 θ

மேற்கண்ட மூன்று முற்றொருமைகளும் முக்கோணவியலின் அடிப்படை முற்றொருமைகள் என அழைக்கப்படுகின்றன.

இம்முற்றொருமைகளைக் கீழ்க்காணுமாறு நிரூபிக்கலாம். 

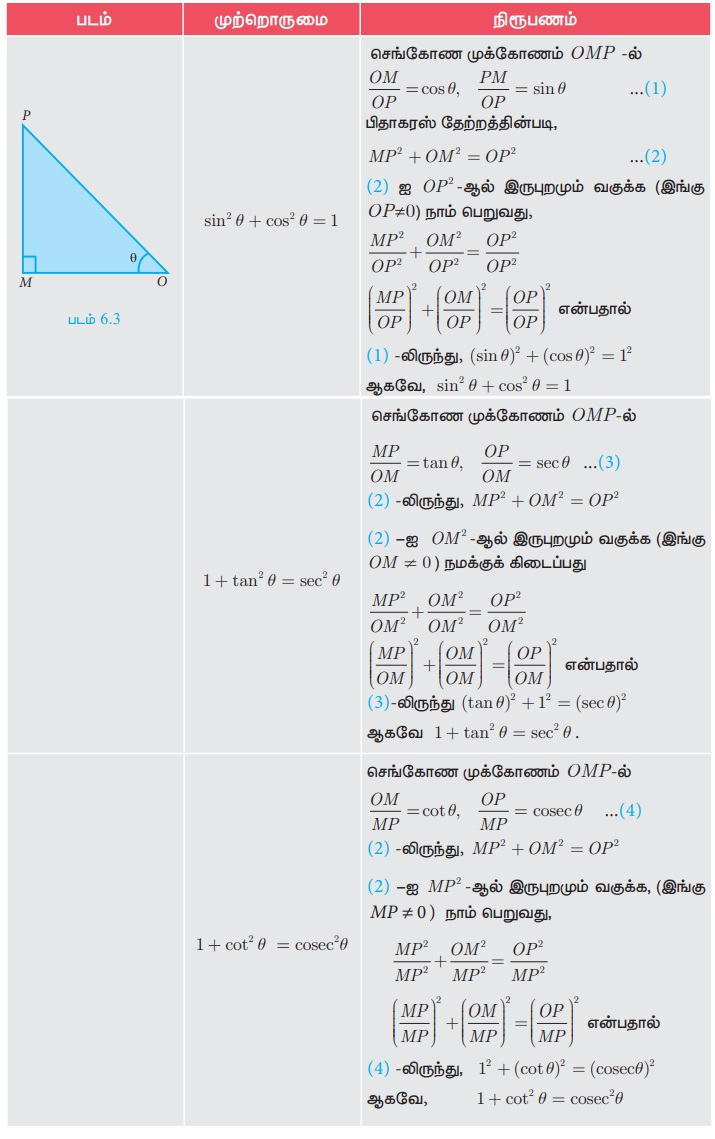
இந்த முக்கோணவியல் முற்றொருமைகளைப் பின்வருமாறு மாற்றி எழுதலாம். 

குறிப்பு  

மேற்கண்ட முக்கோணவியல் முற்றொருமைகள் θ - வின் அனைத்து மதிப்புகளுக்கும் உண்மையாகும். ஆனால், நாம் ஆறு முக்கோணவியல் விகிதக் கோணங்களை 0° < θ < 90° என மட்டும் எடுத்துக்கொள்வோம்.

செயல்பாடு 1

ஒரு வெள்ளைத்தாளில் படம் 6.4 (i) -ல் உள்ளவாறு OX, OY என்ற இரு செங்குத்துக் கோடுகள் O -ல் சந்திக்குமாறு அமைக்கவும். 

OX என்பதை X அச்சாகவும், OY என்பதை Y அச்சாகவும் எடுத்துக்கொள்வோம்.

θ -ன் குறிப்பிட்ட கோணங்களுக்கு sin θ மற்றும் cos θ -ன் மதிப்புகளைச் சரிபார்க்கலாம்.

இங்கு, θ = 30° என்க.

படம் 6.4(ii)-ல் உள்ளவாறு ஏதாவது ஒரு நீளத்திற்கு கோட்டுத் துண்டு OA, ∠AOX = 30° என்றவாறு அமைக்க. B-யில் சந்திக்குமாறு A-யிலிருந்து OX-க்கு ஒரு செங்குத்துக்கோடு வரைக.

இப்பொழுது அளவுகோலைப் பயன்படுத்தி, AB, OB மற்றும் OA -வின் நீளத்தை அளக்கவும்.

விகிதங்கள் AB/OA, OB/OA மற்றும் AB/OB ஆகியவற்றைக் காண்க.

இதிலிருந்து என்ன கிடைக்கிறது? இந்த மதிப்புகளை முக்கோணவியல் அட்டவணை மதிப்புகளுடன் ஒப்பிடலாமா? உங்கள் முடிவு என்னவாக இருக்கும்?

இதேபோல, θ = 45° மற்றும் θ = 60° ஆகிய ' கோணங்களுக்கும் மேற்கண்ட மூன்று மதிப்புகளைக் காண்க. இதன் மூலம் நீங்கள் அறிவது என்ன?

எடுத்துக்காட்டு 6.1

tan 2 θ − sin2 θ = tan 2 θ sin2 θ என்பதை நிரூபிக்கவும்.

தீர்வு

tan 2 θ - sin2 θ = tan2 θ − 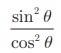. cos2 θ

 = tan 2 θ (1 − cos 2 θ) = tan 2 θ sin2 θ

எடுத்துக்காட்டு 6.2 

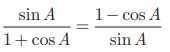என்பதை நிரூபிக்கவும்.

தீர்வு

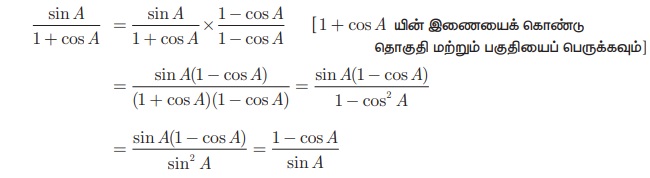
எடுத்துக்காட்டு 6.3 

1 + 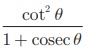 = cosec θ என்பதை நிரூபிக்கவும்.

தீர்வு

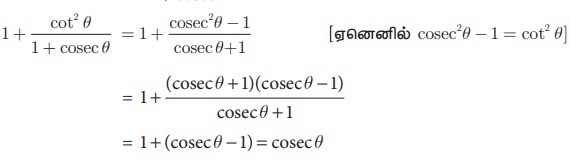
எடுத்துக்காட்டு 6.4 

sec θ − cos θ = tan θ sin θ என்பதை நிரூபிக்கவும்.

தீர்வு

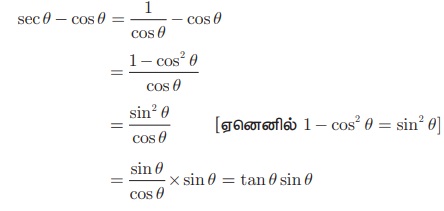
எடுத்துக்காட்டு 6.5

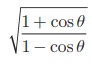 = cosec θ + cot θ என்பதை நிரூபிக்கவும்.

தீர்வு

எடுத்துக்காட்டு 6.6

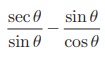 = cot θ என்பதை நிரூபிக்கவும்.

தீர்வு

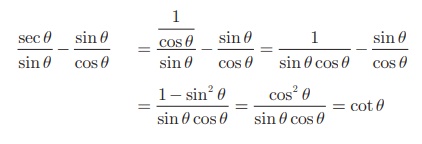
எடுத்துக்காட்டு 6.7 

sin²A cos² B + cos² A sin² B + cos² A cos² B + sin² A sin² B = 1 என்பதை நிரூபிக்கவும். 

தீர்வு 

sin2A cos2 B + cos2 A sin2 B + cos2 A cos2 B + sin2 A sin2 B

 = sin 2 A cos2 B + sin 2 A sin2 B + cos 2 A sin2 B + cos 2 A cos2 B 

 = sin2 A(cos2 B + sin2 B ) + cos2 A(sin2 B + cos 2 B)

 = sin 2 A(1) + cos2 A(1)              (ஏனெனில் sin2 B + cos 2 B = 1)

 = sin 2 A + cos2 A = 1

எடுத்துக்காட்டு 6.8

cos θ + sin θ = √2 cos θ எனில், cos θ − sin θ = √2sin θ என நிரூபிக்க.

தீர்வு 

இப்பொழுது, cos θ + sin θ = √2 cos θ என்பதை இருபுறமும் வர்க்கப்படுத்துக.

(cos θ + sin θ)2 = (√2 cos θ)2

cos 2 θ + sin2 θ + 2 sin θ cos θ = 2 cos2 θ

2 cos2 θ - cos2 θ - sin2 θ = 2 sin θ cos θ

cos 2 θ - sin2 θ = 2 sin θ cos θ

(cos θ + sin θ) (cos θ − sin θ) =2 sin θ cos θ

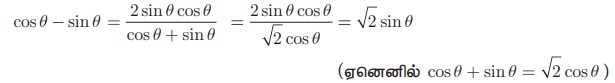
⸫ cos θ − sin θ = √2sin θ.

எடுத்துக்காட்டு 6.9

(cosec θ − sin θ)(sec θ − cos θ)(tan θ + cot θ) =1 என்பதை நிரூபிக்கவும்.

தீர்வு 

(cosec θ − sin θ) (sec θ − cos θ)(tan θ + cot θ)

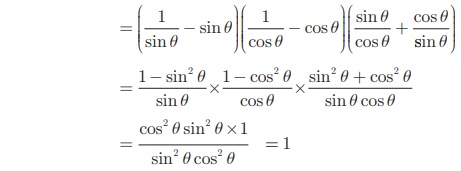
எடுத்துக்காட்டு 6.10

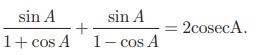என்பதை நிரூபிக்கவும்.

தீர்வு 

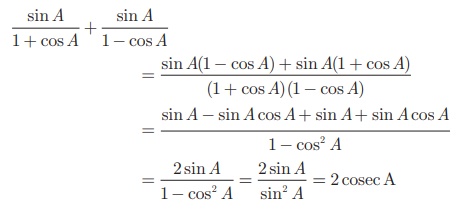
எடுத்துக்காட்டு 6.11

cosec θ +cot θ = P , எனில், cos θ = 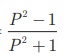 என்பதை நிரூபிக்கவும்.

தீர்வு 

cosec θ +cot θ = P   எனக் கொடுக்கப்பட்டுள்ளது ...(1)

cosec2 θ - cot2 θ =1 (முற்றொருமை)

cosec θ - cot θ = 1 / (cosec θ + cot θ)

எடுத்துக்காட்டு 6.12 

tan2A − tan2 B = 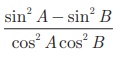  என்பதை நிரூபிக்கவும்.

தீர்வு 

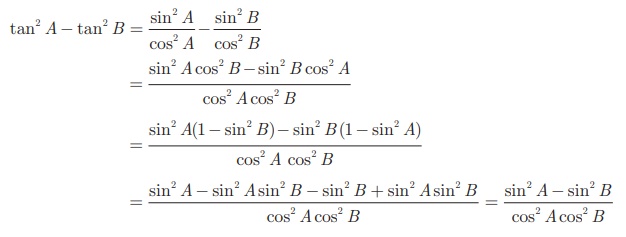
எடுத்துக்காட்டு 6.13 

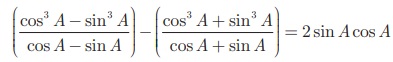என்பதை நிரூபிக்கவும்.

தீர்வு 

எடுத்துக்காட்டு 6.14

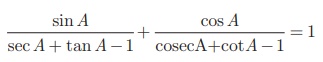என்பதை நிரூபிக்கவும். 

தீர்வு 

எடுத்துக்காட்டு 6.15

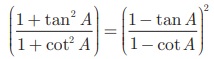எனக் காட்டுக. 

தீர்வு

எடுத்துக்காட்டு 6.16

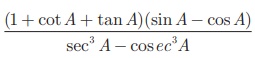 = sin 2 A cos2 A என்பதை நிரூபிக்கவும்.

தீர்வு

எடுத்துக்காட்டு 6.17

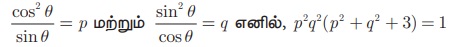என நிரூபிக்க

தீர்வு

முன்னேற்றச் சோதனை

1. முக்கோணவியல் விகிதங்களின் எண்ணிக்கையானது ____.

2. 1 – cos2θ = -----

3. (sec θ + tan θ) (sec θ - tan θ) = ___.

4. (cot θ + cosec θ) (cot θ – cosec θ) = ____. 

5. cos 60° sin 30° + cos 30° sin 60° = ____.

6. tan 60° cos 60° + cot 60° sin 60° = ____. 

7. (tan 45° + cot 45°) + (sec 45° cosec45°) = ____.

8. (i) sec θ = cosec θ எனில், θ = ____.

(ii) cot θ = tan θ எனில், θ = ____.