ஏற்றக்கோணமும் இறக்கக்கோணமும் கொண்ட கணக்குகள்

ஏற்றக்கோணமும் இறக்கக்கோணமும் கொண்ட கணக்குகள் (Problems involving Angle of Elevation and Depression)

பின்வரும் சூழ்நிலையைக் கருத்தில் கொள்வோம். 

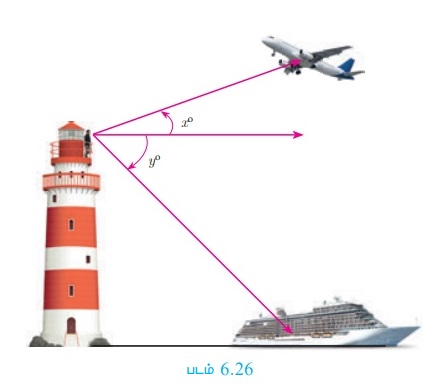
கடற்கரையில் அமைந்துள்ள கலங்கரை விளக்கத்தின் உச்சியின்மீது ஒருவர் நின்றுகொண்டு வானில் பறந்து கொண்டிருக்கின்ற விமானத்தைப் பார்க்கிறார். அதே வேளையில், கடலில் சென்று கொண்டிருக்கின்ற கப்பல் ஒன்றையும் பார்க்கிறார். அவர் விமானத்தை ஏற்றக்கோணத்திலும், கப்பலை இறக்கக்கோணத்திலும் காண்கிறார். இந்த எடுத்துக் காட்டிலிருந்து ஏற்றக்கோணம் மற்றும் இறக்கக் கோணம் ஒரே சூழ்நிலையில் பயன்படுகிறது என்பதை அறிகிறோம்.

படம் 6.26 -ல் x° என்பது ஏற்றக்கோணம் மற்றும் y° என்பது இறக்கக்கோணம் ஆகும்.

இந்தப் பகுதியில் ஏற்றக்கோணமும், இறக்கக்கோணமும் கொடுக்கப்பட்டிருந்தால் அவ்வகைக் கணக்குகளுக்குத் தீர்வு காண முயல்வோம். 

எடுத்துக்காட்டு 6.31 

12 மீ உயரமுள்ள கட்டிடத்தின் உச்சியிலிருந்து மின்சாரக் கோபுர உச்சியின் ஏற்றக்கோணம் 60° மற்றும் அதன் அடியின் இறக்கக் கோணம் 30° எனில், மின்சாரக் கோபுரத்தின் உயரத்தைக் காண்க 

தீர்வு 

படம் 6.27 -ல் AO என்பது கட்டடம். O என்பது கட்டடத்தின் உச்சிப் புள்ளி என்க. மேலும், OA = 12 மீ.

PP' என்பது மின்சாரக் கோபுரம். இதில் P என்பது மின் கோபுரத்தின் உச்சி, P' என்பது மின் கோபுரத்தின் அடி.

P-யின் ஏற்றக்கோணம் ∠MOP = 60° மற்றும் P' -ன் இறக்கக்கோணம் ∠MOP′ = 30° 

மின் கோபுரத்தின் உயரம் PP' = h மீ என்க. 

O வழியாக OM ┴ PP ' வரைக.

MP = PP′ − MP′ = h − OA = h −12

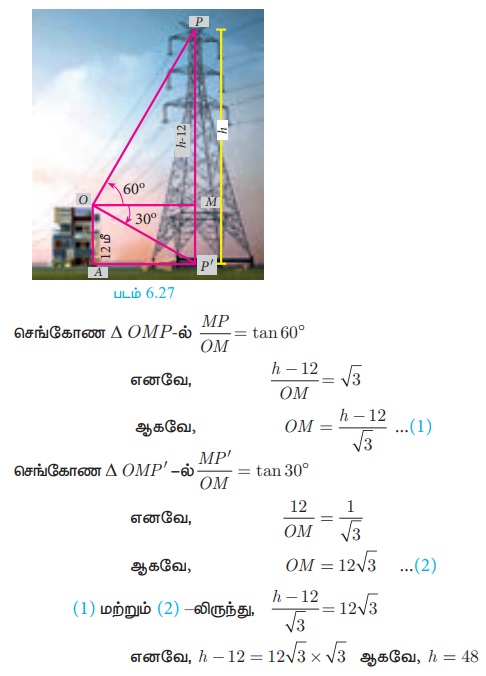
எனவே, மின் கோபுரத்தின் உயரம் = 48 மீ.

எடுத்துக்காட்டு 6.32 

ஒரு கோபுர உச்சியின் மீது 5 மீ உயரமுள்ள கம்பம் பொருத்தி வைக்கப் பட்டுள்ளது. தரையில் உள்ள 'A' என்ற புள்ளியிலிருந்து கம்பத்தின் உச்சியை 60° ஏற்றக்கோணத்திலும், கோபுரத்தின் உச்சியிலிருந்து 'A' என்ற புள்ளியை 45° இறக்கக் கோணத்திலும் பார்த்தால், கோபுரத்தின் உயரத்தைக் காண்க. (√3=1.732)

தீர்வு 

கோபுரத்தின் உயரம் BC என்க. கம்பத்தின் உயரம் CD எனக் கொள்க. 

உற்று நோக்குப் புள்ளி A என்க

மேலும் BC = x மற்றும் AB = y என்க.

படத்தில், 

∠BAD = 60° மற்றும் ∠XCA = 45° = ∠BAC

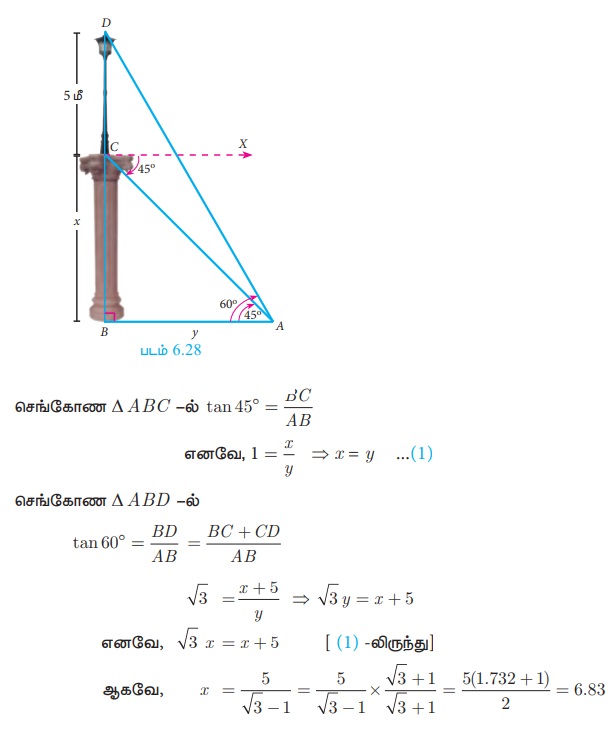
எனவே, கோபுரத்தின் உயரம் = 6.83 மீ. 

எடுத்துக்காட்டு 6.33 

ஒரு தெருவில் உள்ள ஒரு வீட்டின் சன்னலிலிருந்து, (சன்னல் தரைக்கு மேல் h மீ உயரத்தில் உள்ளது) தெருவின் எதிர்ப் பக்கத்தில் உள்ள மற்றொரு வீட்டின் உச்சி, அடி ஆகியவற்றின் ஏற்றக்கோணம், இறக்கக்கோணம் முறையே θ1 மற்றும் θ2 எனில், எதிர்ப்பக்கத்தில் அமைந்த வீட்டின் உயரம் 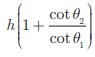என நிரூபிக்க.

தீர்வு 

படத்தில் W என்பது சன்னலிலுள்ள ஒரு புள்ளி என்க. இப்புள்ளியிலிருந்து ஏற்றக்கோணமும், இறக்கக் கோணமும் கணக்கிடப்படுகிறது எனக் கொள்வோம். PQ என்பது எதிர்ப்பக்கத்தில் உள்ள வீடு என்க.

WA என்பது சன்னலிலிருந்து வீட்டிற்கு உள்ள தொலைவாகும்.

சன்னலின் உயரம் = h = AQ (WR = AQ)

PA = xமீ என்க. 

நிரூபிக்கப்பட்டது.

சிந்தனைக் களம் 

உயரம், தொலைவு மற்றும் ஏற்றக்கோணம் காண்பதற்குக் குறைந்தது எத்தனை அளவுகள் தேவை?

முன்னேற்றச் சோதனை

1. உற்றுநோக்குபவரின் கண்ணிலிருந்து பொருளின் ஒரு புள்ளிக்கு வரையப்படும் கோடு ___________ ஆகும். 

2. ஒரு பொருளை உற்று நோக்கும்போது கிடைமட்டக் கோட்டிற்கும் பார்வைக்கோட்டிற்கும் இடைப்பட்ட கோணம் எக்கருவி மூலம் அளவிடப்படுகிறது? 

3. பார்வைக் கோடானது கிடைமட்டக் கோட்டிற்கு மேலே இருக்கும்போது ஏற்படும் கோணம் __________ ஆகும். 

4. செங்குத்தாக உள்ள ஒரு பொருளின் (கோபுரம்) அடியை நோக்கிச் செல்லும்போது அதன் ஏற்றக்கோணம் ______________.

5. பார்வைக்கோடானது கிடைமட்டக் கோட்டிற்குக் கீழே இருக்கும்போது ஏற்படும் கோணம் ____________ ஆகும்.