பலவுள் தெரிவு வினாக்கள்

பயிற்சி 6.5

பலவுள் தெரிவு வினாக்கள்

1. sin2θ + 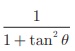  –ன் மதிப்பு

(அ) tan2 θ

(ஆ) 1

(இ) cot2 θ

(ஈ) 0 

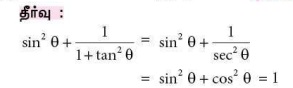
2. tanθ cosec2θ - tan θ - ன் மதிப்பு 

(அ) sec θ

(ஆ) cot2θ

(இ) sin θ

(ஈ) cotθ

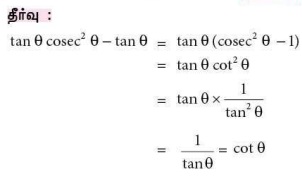
3. (sin a + coseca)2 + (cos a + sec a)2 = k + tan2a + cot2a எனில் k - ன் மதிப்பு 

(அ) 9 

(ஆ) 7

(இ) 5

(ஈ) 3 

4. sin θ + cos θ = a மற்றும் sec θ + cosecθ = b எனில் b (a2 -1) -ன் மதிப்பு 

(அ) 2a 

(ஆ) 3a 

(இ) 0

(ஈ) 2ab

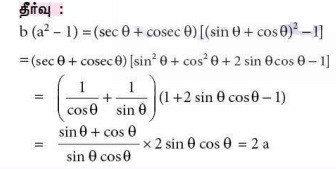
5. 5x = sec θ and 5/x = tan θ எனில் x2 – (1/ x2) -ன் மதிப்பு 

(அ) 25 

(ஆ) 1 / 25 

(இ) 5 

(ஈ) 1

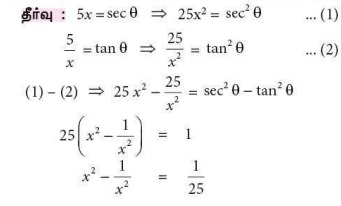
6. sin θ = cos θ, எனில் 2 tan2θ + sin2θ −1 -ன் மதிப்பு

(அ) -3/2

(ஆ) 3/2

(இ) 2/3

(ஈ) -2/3

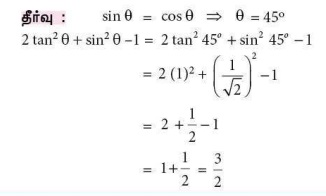
7. x = a tan θ மற்றும் y = b sec θ எனில்

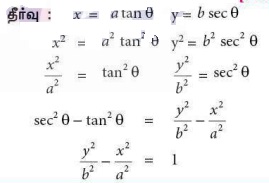
8. (1 + tan θ + sec θ) (1 + cot θ − cosecθ) -ன் மதிப்பு 

(அ) 0 

(ஆ) 1 

(இ) 2

(ஈ) -1 

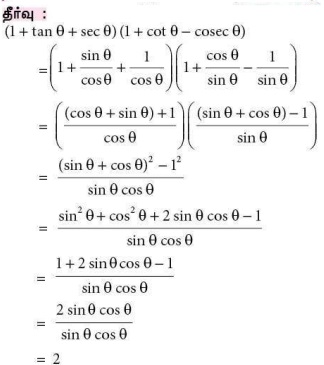
9. a cot θ + b cosecθ = p மற்றும் b cot θ + a cosec θ = q எனில் p² - q² -ன் மதிப்பு

(அ) a2 - b2

(ஆ) b2 - a2

(இ) a2 + b2

(ஈ) b –a

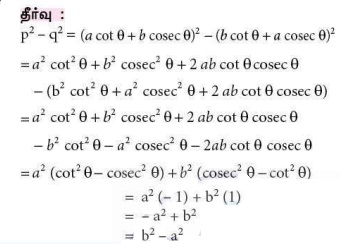
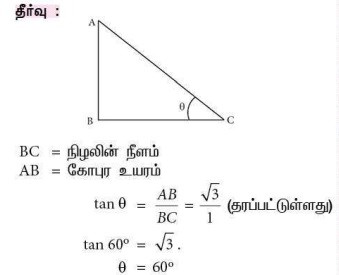
10. ஒரு கோபுரத்தின் உயரத்திற்கும் அதன் நிழலின் நீளத்திற்கும் உள்ள விகிதம் √3 : 1, எனில் சூரியனைக் காணும் ஏற்றக்கோண அளவானது 

(அ) 45° 

(ஆ) 30° 

(இ) 90°

(ஈ) 60° 

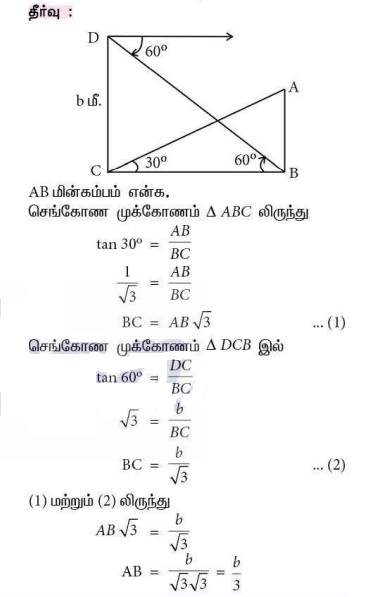
11. ஒரு மின் கம்பமானது அதன் அடியில் சமதளப் பரப்பில் உள்ள ஒரு புள்ளியில் 30° கோணத்தை ஏற்படுத்துகிறது. முதல் புள்ளிக்கு ‘b’ மீ உயரத்தில் உள்ள இரண்டாவது புள்ளியிலிருந்து மின்கம்பத்தின் அடிக்கு இறக்கக்கோணம் 60° எனில் மின் கம்பத்தின் உயரமானது (மீட்டரில்)

(அ) √3b

(ஆ) b/3

(இ) b/2

(ஈ) b/√3

12. ஒரு கோபுரத்தின் உயரம் 60 மீ ஆகும். சூரியனை காணும் ஏற்றக்கோணம் 30° -லிருந்து 45° ஆக உயரும்போது கோபுரத்தின் நிழலானது xமீ குறைகிறது எனில், x-ன் மதிப்பு 

(அ) 41.92 மீ 

(ஆ) 43.92 மீ 

(இ) 43 மீ

(ஈ) 45.6 மீ 

13. பல அடுக்குக் கட்டடத்தின் உச்சியிலிருந்து 20 மீ உயரமுள்ள கட்டடத்தின் உச்சி, அடி ஆகியவற்றின் இறக்கக்கோணங்கள் முறையே 30° மற்றும் 60° எனில் பல அடுக்குக் கட்டடத்தின் உயரம் மற்றும் இரு கட்டடங்களுக்கு இடையேயுள்ள தொலைவானது (மீட்டரில்)

(அ) 20, 10√3

(ஆ) 30, 5√3

(இ) 20, 10

(ஈ) 30, 10√3

14. இரண்டு நபர்களுக்கு இடைப்பட்ட தொலைவு x மீ ஆகும். முதல் நபரின் உயரமானது இரண்டாவது நபரின் உயரத்தைப் போல இரு மடங்காக உள்ளது. அவர்களுக்கு இடைப்பட்ட தொலைவு நேர்கோட்டின் மையப் புள்ளியிலிருந்து இரு நபர்களின் உச்சியின் ஏற்றக் கோணங்கள் நிரப்புக்கோணங்கள் எனில், குட்டையாக உள்ள நபரின் உயரம் (மீட்டரில்) காண்க. 

(அ) √2 x

(ஆ) x / 2√2

(இ) x / √2

(ஈ) 2x

15. ஓர் ஏரியின் மேலே h மீ உயரத்தில் உள்ள ஒரு புள்ளியிலிருந்து மேகத்திற்கு உள்ள ஏற்றக்கோணம் β. மேக பிம்பத்தின் இறக்கக்கோணம் 45° எனில், ஏரியில் இருந்து மேகத்திற்கு உள்ள உயரமானது (மீட்டரில்) 

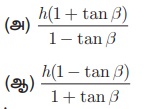
(இ) h tan (45° − β)

(ஈ) இவை ஒன்றும் இல்லை