Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї | Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї | Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї | 10th Mathematics : UNIT 6 : Trigonometry
10Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 6 : Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї
Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї
Я«ЅЯ«»Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї (Heights and Distances)
Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ«ЙЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї, Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я«ЙЯ«Е Я«фЯ»іЯ«░Я»ЂЯ«ЪЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ»ЄЯ«░Я«┐Я«ЪЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЁЯ«│Я«еЯ»ЇЯ«цЯ»Ђ Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ««Я«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ«▓Я«ЙЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я««Я»Ї, Я««Я«▓Я»ѕ, Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЪЯ««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я«░Я««Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї, Я«ЋЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«░Я»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«ЪЯ«▓Я«┐Я«▓Я»Ї Я««Я«┐Я«цЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ«фЯ»ЇЯ«фЯ«▓Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«єЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЋЯ«▓Я««Я»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«еЯ»ЇЯ«ц Я«ЁЯ«▒Я«┐Я«хЯ»Ђ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ Я«ЅЯ«»Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«хЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«ЁЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«Ъ Я«хЯ«ЙЯ«┤Я»ЇЯ«хЯ«┐Я«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«џЯ«┐Я«▓ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЅЯ«»Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«▒Я»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«еЯ«ЙЯ««Я»Ї Я«њЯ«░Я»ЂЯ«џЯ«┐Я«▓ Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«ЋЯ«│Я»ѕ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.
Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ (Line of Sight)
Я«еЯ«ЙЯ««Я»Ї Я«њЯ«░Я»Ђ Я«фЯ»іЯ«░Я»ЂЯ«│Я»ѕ Я«ЅЯ«▒Я»ЇЯ«▒Я»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«еЯ««Я«цЯ»Ђ Я«ЋЯ«БЯ»ЇЯ«БЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ»іЯ«░Я»ЂЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
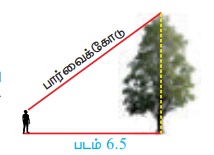
Я«цЯ«┐Я«»Я»ІЯ«ЪЯ«▓Я»ѕЯ«ЪЯ»Ї
Я«цЯ«┐Я«»Я»ІЯ«ЪЯ«▓Я»ѕЯ«ЪЯ»Ї Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«░Я»ЂЯ«хЯ«┐ Я«њЯ«░Я»Ђ Я«фЯ»іЯ«░Я»ЂЯ«│Я»ѕ Я«ЅЯ«▒Я»ЇЯ«▒Я»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ«хЯ«░Я«┐Я«ЕЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї, Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ Я«ЁЯ«│Я«хЯ«┐Я«ЪЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«цЯ«┐Я«»Я»ІЯ«ЪЯ«▓Я»ѕЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«џЯ«ЋЯ»ЇЯ«ЋЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я»ЂЯ«ЪЯ«ЕЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«цЯ«џЯ»Ї Я«џЯ«ЋЯ»ЇЯ«ЋЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«│Я«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я»Ї. Я«хЯ«┐Я«░Я»ЂЯ««Я»ЇЯ«фЯ«┐Я«» Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ Я«ЁЯ«│Я«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ, Я«цЯ»іЯ«▓Я»ѕЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я»ѕ Я«ЁЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«хЯ»ѕЯ«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«│Я«хЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ»ІЯ«▓Я«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я»Ї.

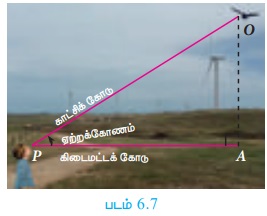
Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (Angle of Elevation)
Я«њЯ«░Я»Ђ Я«фЯ»іЯ«░Я»ЂЯ«│Я»Ї Я«еЯ««Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»Є Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«ЋЯ«┐Я«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї, Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ»іЯ«░Я»ЂЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ, Я«еЯ«ЙЯ««Я»Ї Я«цЯ«▓Я»ѕЯ«»Я»ѕ Я«џЯ«▒Я»ЇЯ«▒Я»Є Я«ЅЯ«»Я«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«еЯ«┐Я«▓Я»ѕЯ«»Я»Є Я«єЯ«ЋЯ»ЂЯ««Я»Ї (Я«фЯ«ЪЯ««Я»Ї 6.7Я«љ Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї).
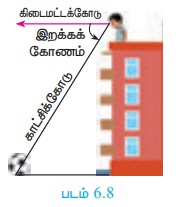
Я«ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ««Я»Ї (Angle of Depression)
Я«њЯ«░Я»Ђ Я«фЯ»іЯ«░Я»ЂЯ«│Я»Ї Я«еЯ««Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ђЯ«┤Я»Є Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ»іЯ«░Я»ЂЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ Я«еЯ«ЙЯ««Я»Ї Я«цЯ«▓Я»ѕЯ«»Я»ѕ Я«џЯ«▒Я»ЇЯ«▒Я»Є Я«цЯ«ЙЯ«┤Я»ЇЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«еЯ«┐Я«▓Я»ѕЯ«»Я»Є Я«єЯ«ЋЯ»ЂЯ««Я»Ї (Я«фЯ«ЪЯ««Я»Ї 6.8Я«љ Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї).
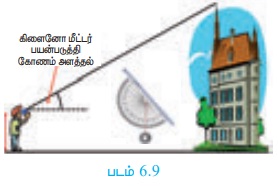
Я«ЋЯ«┐Я«│Я»ѕЯ«ЕЯ»І Я««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»Ї (Clinometer)
Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«┐Я«│Я»ѕЯ«ЕЯ»І Я««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«░Я»ЂЯ«хЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
┬и Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ»іЯ«░Я»ЂЯ«│Я«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«│Я«хЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
h1 > h2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, ╬▒ > ╬▓ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
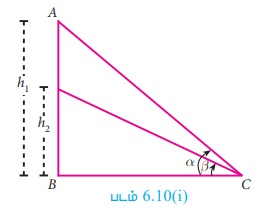
┬и Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЪЯ««Я»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«»Я»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«еЯ«ЋЯ«░Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
d2 < d1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, ╬▓ > ╬▒ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
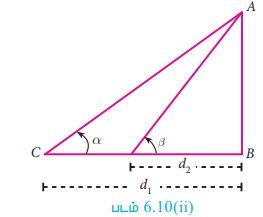
Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ 2
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ»ѓЯ«┤Я»ЇЯ«еЯ«┐Я«▓Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«хЯ«░Я»ѕЯ«»Я«хЯ»ЂЯ««Я»Ї.

Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї (Problems involving Angle of Elevation)
Я«ЄЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї, Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«ЁЯ«▒Я«┐Я«хЯ»ІЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.18
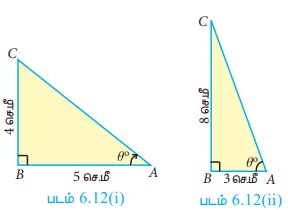
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї РѕаBAC -Я«љ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. (tan 38.7┬░ = 0.8011, tan 69.4┬░ = 2.6604)
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
(i) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ ABC -Я«▓Я»Ї (Я«фЯ«ЪЯ««Я»Ї 6.12 (i) Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї)
tan ╬И = Я«јЯ«цЯ«┐Я«░Я»ЇЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї / Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї = 4/5
tan ╬И = 0.8
РЄњ ╬И = 38.7┬░ (РИф tan 38.7┬░ = 0.8011)
РИФ РѕаBAC = 38.7┬░
(ii) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ ABC -Я«▓Я»Ї (Я«фЯ«ЪЯ««Я»Ї 6.12 (ii) Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї)
tan ╬И = 8/3
tan ╬И = 2.66
РЄњ ╬И = 69.4┬░ (РИф tan 69.4┬░ = 2.6604)
РИФ РѕаBAC = 69.4┬░
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.19
Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я««Я»Ї Я«цЯ«░Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«цЯ«░Я»ѕЯ«»Я«┐Я«▓Я»Ї 48 Я««Я»ђ. Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ІЯ«фЯ»ЂЯ«░ Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї 30┬░ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї PQ Я«јЯ«ЕЯ»ЇЯ«Ћ. PQ = h Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«░Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ R - Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ QR Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ PQR-Я«▓Я»Ї РѕаPRQ = 30┬░
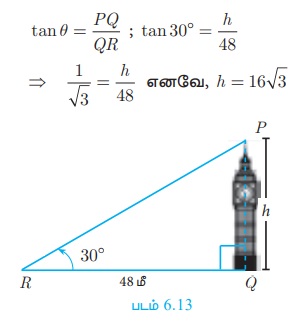
Я«єЯ«ЋЯ«хЯ»Є, Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї 16Рѕџ3 Я««Я»ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.20
Я«цЯ«░Я»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї 75 Я««Я»ђ Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ«▒Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«њЯ«░Я»Ђ Я«еЯ»ѓЯ«▓Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«▓Я«┐Я«ЋЯ««Я«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ«░Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї Я«фЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«еЯ»ѓЯ«▓Я»Ї Я«цЯ«░Я»ѕЯ«»Я»ЂЯ«ЪЯ«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ««Я»Ї 60┬░ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«еЯ»ѓЯ«▓Я«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. (Я«еЯ»ѓЯ«▓Я»ѕ Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ«ЙЯ«Ћ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я«хЯ»ЂЯ««Я»Ї).
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«цЯ«░Я»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї AB = 75 Я««Я»ђ Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«еЯ»ѓЯ«▓Я«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї AC Я«јЯ«ЕЯ»ЇЯ«Ћ.
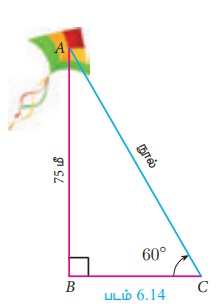
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ ABC-Я«▓Я»Ї, РѕаACB = 60┬░
sin ╬И = AB/AC
sin 60┬░ = 75/AC
Рѕџ3/2 = 75/AC Я«єЯ«ЋЯ«хЯ»Є, AC = 150/Рѕџ3 = 50Рѕџ3
Я«јЯ«ЕЯ«хЯ»Є, Я«еЯ»ѓЯ«▓Я«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 50Рѕџ3 Я««Я»ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.21
Я«ЄЯ«░Я»Ђ Я«ЋЯ«фЯ»ЇЯ«фЯ«▓Я»ЇЯ«ЋЯ«│Я»Ї Я«ЋЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«░Я»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї Я«ЋЯ«ЪЯ«▓Я«┐Я«▓Я»Ї Я«фЯ«»Я«БЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«░Я»Ђ Я«ЋЯ«фЯ»ЇЯ«фЯ«▓Я»ЇЯ«ЋЯ«│Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«░Я»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 30┬░ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 45┬░ Я«єЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«░Я»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї 200 Я««Я»ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ«░Я»Ђ Я«ЋЯ«фЯ»ЇЯ«фЯ«▓Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. (Рѕџ3=1.732)
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«░Я»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ««Я»Ї AB Я«јЯ«ЕЯ»ЇЯ«Ћ. C Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї D Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЄЯ«░Я»Ђ Я«ЋЯ«фЯ»ЇЯ«фЯ«▓Я»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ.
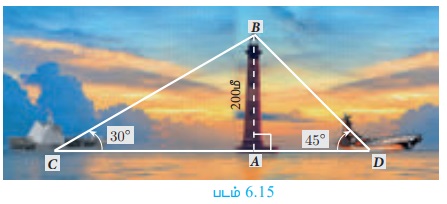
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, AB = 200 Я««Я»ђ.
РѕаACB = 30┬░, РѕаADB = 45┬░
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ BAC-Я«▓Я»Ї
tan 30┬░ = AB/AC
1/Рѕџ3 = 200/AC РЄњ AC = 200Рѕџ3 ...(1)
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ BAD-Я«▓Я»Ї tan 45┬░ = AB/AD
1 = 200/AD РЄњ AD = 200 ...(2)
Я«цЯ«▒Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, CD = AC + AD = 200Рѕџ3 + 200 [(1) , (2) -Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ]
CD = 200(Рѕџ3 + 1) = 200 ├Ќ 2. 732 = 546.4
Я«ЄЯ«░Я»Ђ Я«ЋЯ«фЯ»ЇЯ«фЯ«▓Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ 546.4 Я««Я»ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.22
Я«цЯ«░Я»ѕЯ«»Я«┐Я«ЕЯ»ЇЯ««Я»ђЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 30 Я««Я»ђ Я«ЅЯ«»Я«░Я««Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ЄЯ«▓Я»ЂЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 45┬░ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 60┬░ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. (Рѕџ3=1.732)
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї AC Я«јЯ«ЕЯ»ЇЯ«Ћ.
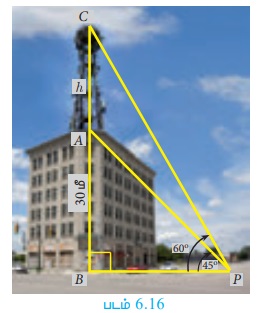
Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї AB Я«јЯ«ЕЯ»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї AC = h Я««Я»ђ, AB = 30 Я««Я»ђ
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ CBP-Я«▓Я»Ї РѕаCPB = 60┬░
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ ABP-Я«▓Я»Ї, РѕаAPB = 45┬░

h = Рѕњ 30(Рѕџ3 - 1) = 30 (1.732 РђЊ 1) = 30(0.732) = 21.96
Я«јЯ«ЕЯ«хЯ»Є, Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї = 21.96 Я««Я»ђ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.23
Я«њЯ«░Я»Ђ Я«ЋЯ«ЙЯ«▓Я»ЇЯ«хЯ«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«ЋЯ«░Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«цЯ»іЯ«▓Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«џЯ«┐Я«ЋЯ»Ї Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЋЯ«ЙЯ«▓Я»ЇЯ«хЯ«ЙЯ«»Я«┐Я«ЕЯ»Ї Я««Я«▒Я»Ђ Я«ЋЯ«░Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«ЋЯ»ІЯ«фЯ»ЂЯ«░ Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї 58┬░ Я«єЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЁЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«хЯ«┐Я«▓Я«ЋЯ«┐ Я«њЯ«░Я»Є Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї 20 Я««Я»ђ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«џЯ»єЯ«ЕЯ»ЇЯ«▒Я«хЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«ЋЯ»ІЯ«фЯ»ЂЯ«░ Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї 30┬░ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї, Я«ЋЯ«ЙЯ«▓Я»ЇЯ«хЯ«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЋЯ«▓Я«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. (tan 58┬░ = 1.6003)
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«цЯ»іЯ«▓Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«џЯ«┐Я«ЋЯ»Ї Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї AB Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«ЋЯ«ЙЯ«▓Я»ЇЯ«хЯ«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЋЯ«▓Я««Я»Ї BC Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, CD = 20 Я««Я»ђ.
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ ABC -Я«▓Я»Ї
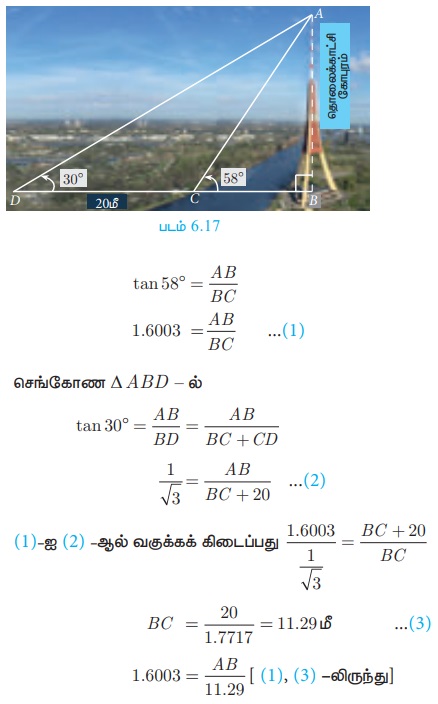
AB = 18.07
Я«јЯ«ЕЯ«хЯ»Є, Я«ЋЯ»ІЯ«фЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї = 18.07 Я««Я»ђ Я«ЋЯ«ЙЯ«▓Я»ЇЯ«хЯ«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЋЯ«▓Я««Я»Ї = 11.29 Я««Я»ђ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.24
Я«њЯ«░Я»Ђ Я«хЯ«┐Я««Я«ЙЯ«ЕЯ««Я»Ї G-Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 24┬░ Я«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«цЯ»Ї Я«цЯ«ЙЯ«ЎЯ»ЇЯ«ЋЯ«┐ 250 Я«ЋЯ«┐.Я««Я»ђ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ H-Я«љ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї H-Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 55┬░ Я«хЯ«┐Я«▓Я«ЋЯ«┐ 180 Я«ЋЯ«┐.Я««Я»ђ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ J-Я«љ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
(i) G-Я«ЕЯ»Ї Я«хЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ H-Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Е?
(ii) G-Я«ЕЯ»Ї Я«ЋЯ«┐Я«┤Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ H-Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Е?
(iii) H-Я«ЕЯ»Ї Я«хЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ J-Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Е?
(iv) H-Я«ЕЯ»Ї Я«ЋЯ«┐Я«┤Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ J-Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Е?
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
(i) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ GOH-Я«▓Я»Ї, cos 24┬░ = OG/GH
0.9135 = OG/250; OG = 228.38 Я«ЋЯ«┐.Я««Я»ђ
G-Я«ЕЯ»Ї Я«хЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ H-Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ = 228.38 Я«ЋЯ«┐.Я««Я»ђ.
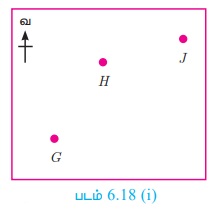
(ii) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ GOH -Я«▓Я»Ї,
sin 24┬░ = OH/GH
0. 4067 = OH/250; OH= 101. 68
G-Я«ЕЯ»Ї Я«ЋЯ«┐Я«┤Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ H-Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ = 101.68 Я«ЋЯ«┐.Я««Я»ђ.

(iii) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ HIJ-Я«▓Я»Ї
sin 11┬░ = IJ/HJ
0. 1908 = IJ/180; IJ = 34. 34 Я«ЋЯ«┐.Я««Я»ђ.
H-Я«ЕЯ»Ї Я«хЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ J-Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ = 34.34 Я«ЋЯ«┐.Я««Я»ђ.
(iv) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ HIJ-Я«▓Я»Ї,
cos 11┬░ = HI/HJ
0. 9816 = HI / 180; HI = 176. 69 Я«ЋЯ«┐.Я««Я»ђ
H-Я«ЕЯ»Ї Я«ЋЯ«┐Я«┤Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ J-Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ = 176.69 Я«ЋЯ«┐.Я««Я»ђ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.25
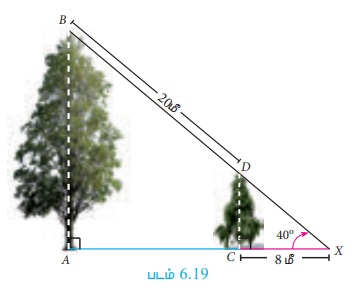
Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«њЯ«░Я»Ђ Я«џЯ««Я«цЯ«│Я«цЯ»Ї Я«цЯ«░Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я«цЯ«░Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ X Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЄЯ«░Я»Ђ Я««Я«░ Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»ЂЯ««Я»Ї 40┬░ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ X -Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ«┐Я«▒Я«┐Я«» Я««Я«░Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ 8 Я««Я»ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ 20 Я««Я»ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
(i) Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ X-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«џЯ«┐Я«▒Я«┐Я«» Я««Я«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ
(ii) Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ (cos 40┬░ = 0.7660) Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«фЯ»єЯ«░Я«┐Я«» Я««Я«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї AB Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«џЯ«┐Я«▒Я«┐Я«» Я««Я«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї CD Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«цЯ«░Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ X Я«јЯ«ЕЯ»ЇЯ«Ћ.
(i) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ XCD-Я«▓Я»Ї
cos 40┬░= CX/XD
XD = 8 / 0.7660 = 10. 44 Я««Я»ђ
Я«јЯ«ЕЯ«хЯ»Є, Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ X - Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«џЯ«┐Я«▒Я«┐Я«» Я««Я«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ
XD = 10.44 Я««Я»ђ
(ii) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б ╬ћ XAB-Я«▓Я»Ї
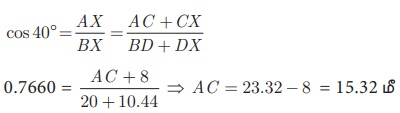
Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ AC = 15.32 Я««Я»ђ.
Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«│Я««Я»Ї
1. Я«ЅЯ«»Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«јЯ«еЯ»ЇЯ«ц Я«хЯ«ЋЯ»ѕЯ«»Я«ЙЯ«Е Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї?
2. Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«┐Я«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«јЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї?
3. Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЈЯ«▒Я»ЇЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї,
(i) Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї
(ii) Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я«┐Я«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї
Я«јЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ«хЯ«┐Я«»Я«▓Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.