Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї РђЊ Я«ЊЯ«░Я»Ї Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ««Я»Ї | Я«фЯ«░Я»ЂЯ«хЯ««Я»Ї 1 Я«ЁЯ«▓Я«ЋЯ»Ђ 2 | 6 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї | 6th Maths : Term 1 Unit 2 : Introduction To Algebra
6 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«фЯ«░Я»ЂЯ«хЯ««Я»Ї 1 Я«ЁЯ«▓Я«ЋЯ»Ђ 2 : Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї РђЊ Я«ЊЯ«░Я»Ї Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ««Я»Ї
Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
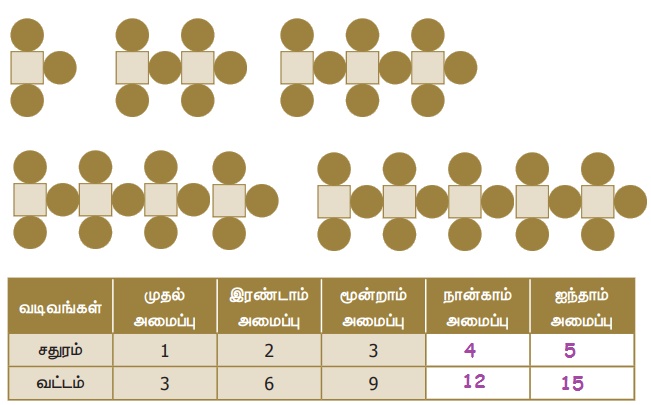
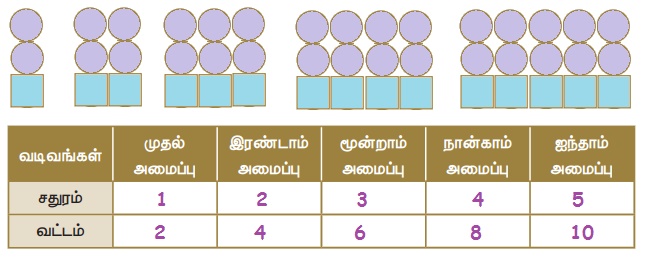
Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«єЯ«░Я«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї Я«јЯ«│Я«┐Я«цЯ«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ»ІЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»ЇЯ«цЯ«ЋЯ»ѕЯ«» Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ«ЙЯ«░Я«Б Я«ЋЯ«ЙЯ«░Я«┐Я«»Я«цЯ»ЇЯ«цЯ»ІЯ«ЪЯ»Ђ Я«іЯ«ЋЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒ Я«цЯ«┐Я«▒Я«ЕЯ»ѕ Я«хЯ«│Я«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ«░Я«┐Я«»Я«ЙЯ«Ћ Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ»Ђ Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«цЯ«┐Я«▒Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒ Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«»Я«▓Я«┐Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ,
1, 2, 3, 4, 5, 6, 7, 8, 9, 10... Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.
Я«ЄЯ«еЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«хЯ«ЕЯ«┐Я«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, 1 Я«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«јЯ«БЯ»Ї, 2 Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї, 3 Я«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«јЯ«БЯ»Ї, 4 Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒Я«┐Я«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЄЯ«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«њЯ«▒Я»ЇЯ«▒Я»ѕ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«░Я»ЂЯ««Я»Ї Я«јЯ«Е Я«ЁЯ«▒Я«┐Я«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї 12, 8, 4,... Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї, Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«БЯ»ѕ Я«ЅЯ«ЕЯ»ЇЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЋЯ»ѓЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я«Й? Я«јЯ«│Я«┐Я««Я»ѕЯ«»Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«њЯ«хЯ»ЇЯ«хЯ»ІЯ«░Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї 4Я«љЯ«ЋЯ»Ї Я«ЋЯ«┤Я«┐Я«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«јЯ«БЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, 4Я«єЯ«хЯ«цЯ»Ђ Я«јЯ«БЯ»Ї '0' Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я«ЙЯ«Е, Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ѕ Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЁЯ«▒Я«┐Я«» Я«ЅЯ«цЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«фЯ«┐Я«░Я«┐Я«хЯ»Є Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЕЯ»ЇЯ«▒Я»ѕЯ«» Я«ЋЯ«ЙЯ«▓Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«хЯ«ЎЯ»ЇЯ«ЋЯ«┐, Я«ЋЯ«ЙЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я»ЂЯ«цЯ«┐ Я«еЯ«┐Я«▒Я»ЂЯ«хЯ«ЕЯ««Я»Ї, Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«▓Я»Ї, Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»Ї, Я«ЁЯ«▒Я«┐Я«хЯ«┐Я«»Я«▓Я»Ї, Я«фЯ»іЯ«▒Я«┐Я«»Я«┐Я«»Я«▓Я»Ї, Я«ЅЯ«▒Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«▓ Я«цЯ»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я««Я»ЂЯ«»Я«▓Я»ЇЯ«Ћ
РЌЈ Я«ЋЯ»ђЯ«┤Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«ЅЯ«▒Я»ЇЯ«▒Я»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«хЯ«┐Я«ЪЯ»ѕЯ«»Я«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
(i) 5, 8, 11, 14, 17, 20, 23, 26
(ii) 15873 ├Ќ 7 = 111111 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 15873 ├Ќ 14 = 222222 Я«јЯ«ЕЯ«┐Я«▓Я»Ї
15873 ├Ќ 21 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 15873 ├Ќ 28 Я«љЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
15873 ├Ќ 21 = 333333
15873 ├Ќ 28 = 444444
РЌЈ Я«ЋЯ»ђЯ«┤Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЅЯ«▒Я»ЇЯ«▒Я»ЂЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ, Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я»ѕ Я«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ»ЂЯ«Ћ.
РЌЈ Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«фЯ»Ї Я«фЯ»ЂЯ«цЯ«┐Я«» Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐, Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«Ћ.
1. Я«јЯ«БЯ»Ї Я«џЯ»єЯ«»Я«▓Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
Я««Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї Я«ЄЯ«»Я«▓Я«┐Я«▓Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЊЯ«░Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ»ѕ 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 1 Я«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я«јЯ«ЕЯ»ЇЯ«Е Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«▒Я»ЇЯ«▒Я»ІЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, 57 ├Ќ 1 = 57 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 43 ├Ќ 0 = 0. Я««Я»ЂЯ«ЕЯ»ЇЯ«фЯ»Ђ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«ц Я«ЄЯ«еЯ»ЇЯ«ц Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЄЯ«еЯ»ЇЯ«ц Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«јЯ«ЕЯ«хЯ»Є "Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЊЯ«░Я»Ї Я«јЯ«БЯ»Ї" ├Ќ 1 = "Я«ЁЯ«цЯ»Є Я«јЯ«БЯ»Ї" Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї, Я«цЯ«ЋЯ«хЯ«▓Я»ЇЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я«јЯ«│Я«┐Я««Я»ѕЯ«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«ц Я«хЯ«┤Я«┐ Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я««Я»ЄЯ«▓Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»ѕ n ├Ќ 1 = n, Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ n Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЊЯ«░Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЪЯ«цЯ»ЂЯ«фЯ»ЂЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ 'n' Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЊЯ«░Я»Ї Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«хЯ«▓Я«цЯ»ЂЯ«фЯ»ЂЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«јЯ«БЯ»Ї Я«ЁЯ«цЯ»Є 'n' Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»ЂЯ«хЯ»Є, Я«еЯ«ЙЯ««Я»Ї Я«џЯ«░Я«┐Я«»Я«ЙЯ«Е Я«ЋЯ»ѓЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ«цЯ«▓Я»ѕ Я«ЅЯ«▒Я»ЂЯ«цЯ«┐ Я«џЯ»єЯ«»Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, Я«еЯ«ЙЯ««Я»Ї 'n' Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я««Я«ЙЯ«▒Я«┐ Я«јЯ«ЕЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я««Я«ЙЯ«▒Я«┐ (Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ Я«єЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«▓ Я«џЯ«┐Я«▒Я«┐Я«» Я«јЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»Ї РђўnРђЎ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ РђўxРђЎ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЊЯ«░Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«џЯ»Ї Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«ц Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. n ├Ќ 1 = n Я«ЄЯ«▓Я»Ї, 1 Я«єЯ«ЕЯ«цЯ»Ђ Я««Я«ЙЯ«▒Я«ЙЯ«ц Я«јЯ«БЯ»ЇЯ««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЄЯ«цЯ»ѕ Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я«јЯ«ЕЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
7 + 9 = 9 + 7
57 + 43 = 43 + 57
123 + 456 = 456 + 123
7098 + 2018 = 2018 + 7098
35784 + 481269841 = 481269841 + 35784
Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ a + b = b + a Я«јЯ«ЕЯ«џЯ»Ї Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я«јЯ«│Я«┐Я««Я»ѕЯ«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ РђўaРђЎ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Рђўb' Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. РђўaРђЎ Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»Є Я«јЯ«БЯ»ЇЯ«БЯ»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»ЂЯ««Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ»ЄЯ«фЯ»ІЯ«▓Я»Ї РђўbРђЎ Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»ЂЯ««Я»Ї Я«њЯ«░Я»Є Я«јЯ«БЯ»ЇЯ«БЯ»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, 'a' Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Рђўb' Я«њЯ«░Я»Є Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«»Я«цЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ.
Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Є, a ├Ќ b = b ├Ќ a Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«ЁЯ«│Я«┐Я«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«»Я«▓Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ: Я«ЋЯ«┤Я«┐Я«цЯ»ЇЯ«цЯ«▓Я«┐Я«▓Я»Ї '7 РђЊ 3' Я«љ '3 РђЊ 7' Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я«ЙЯ«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є 'a РђЊ b' Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 'b РђЊ a' Я«єЯ«ЋЯ«┐Я«»Я«Е Я«џЯ««Я««Я«▓Я»ЇЯ«▓.