எண்ணுதலில் அடிப்படைக் கொள்கைகள்

எண்ணுதலில் அடிப்படைக் கொள்கைகள்

எண்ணுதலில் சில அடிப்படை உத்திகள் உள்ளன. பொருட்களை வரிசைப்படுத்துதல் அல்லது தெரிவு செய்தல் போன்ற அந்த உத்திகள் பல்வேறு வழிகளின் மூலமாக எண்களைத் தீர்மானிக்க உதவுகிறது. இதன் அடிப்படையில் அமைந்த சில அடிப்படை எண்ணுதல் கொள்கைகள் கீழே கொடுக்கப்பட்டுள்ளன. 

1. எண்ணுதலில் கூட்டல் கொள்கை

ஒன்றையொன்று சார்ந்திராத இரண்டு செயல்பாடுகள் முறையே m வழிகளில் அல்லது n வழிகளில் செயல்பட முடியும் எனில், பிறகு அந்த இரண்டு செயல்பாடுகளும் (m + n) வழிகளில் செயல்பட முடியும்.

பின்வரும் சூழ்நிலை எண்ணுவதில் கூட்டல் கொள்கையினைப் பற்றிப் நாம் மேலும் நன்கு புரிந்துகொள்ளலாம்.

சூழ்நிலை:

எட்டாம் வகுப்பில் 16 மாணவர்கள் மற்றும் 9 மாணவிகள் பயில்கின்றனர். அவர்களில் ஒரு மாணவரையோ ஒரு மாணவியையோ வகுப்புத் தலைவராகத் தேர்ந்தெடுக்க ஆசிரியர் விரும்புகிறார் எனில், ஆசிரியர் எத்தனை வழிகளில் வகுப்புத் தலைவரைத் தேர்ந்தெடுக்க முடியும் என்பதைப் பார்ப்போம். 

ஆசிரியர் கீழ்க்கண்ட வழிகளில் ஏதேனும் ஒரு வழியில் வகுப்புத் தலைவரைத் தேர்ந்தெடுக்க முடியும். 

(i) முதல் வாய்ப்பில், 16 மாணவர்களிலிருந்து 1 மாணவரைத் தேர்ந்தெடுக்க 16 வழிகள் உள்ளன. 

(ii) இரண்டாவது வாய்ப்பில், 9 மாணவிகளிலிருந்து 1 மாணவியைத் தேர்ந்தெடுக்க 9 வழிகள் உள்ளன.

ஆகவே, வகுப்பிலுள்ள 25 மாணவர்களில் (16 மாணவர்கள் + 9 மாணவிகள்) 1 மாணவரை அல்லது 1 மாணவியை வகுப்புத் தலைவராகத் தேர்ந்தெடுக்க ஆசிரியருக்கு 25 வெவ்வேறு விதமான வழிகள் உள்ளன.

இதிலிருந்து நாம் அறிந்து கொள்வது, A எனும் ஒரு செயல் m வழிகளிலும், B எனும் மற்றொரு செயல் n வழிகளிலும் செயல்படுகிறது, மேலும் இந்த இரண்டு செயல்களும் ஒரே சமயத்தில் செயல்பட முடியாது எனில் செயல் A அல்லது செயல் B ஆனது (m + n ) வழிகளில் செயல்படும் என்பதாகும்.

பின்வரும் எடுத்துக்காட்டு மூலம் இதனை மேலும் நன்கு புரிந்துகொள்ளலாம்.

எடுத்துக்காட்டு 7.1

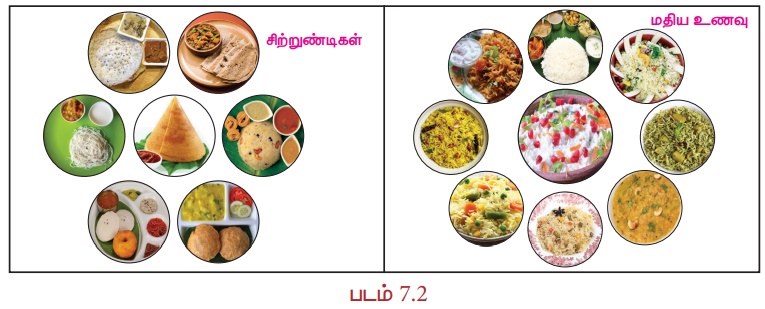
நீங்கள் ஒரு உணவு விடுதியில் சாப்பிடுவதற்கு செல்வதாகக் கொள்வோம். அந்த உணவு விடுதியில் கீழே படம் 7.2இல் கொடுக்கப்பட்டுள்ளது போன்று பல்வேறு விதமான உணவு வகைகள் உள்ளன. உங்களுக்குத் தேவையான ஒரு சிற்றுண்டி உணவையோ அல்லது ஒரு மதிய உணவையோ சாப்பிடுவதற்கு எடுத்துக்கொள்ள எத்தனை விதமான வழிகள் உள்ளது?

தீர்வு :

கொடுக்கப்பட்டுள்ள படம் 7.2 இன் மூலம் நாம் அறிவது, 

(i) 1 சிற்றுண்டியைத் தேர்ந்தெடுக்க 7 வழிகளும் 

(ii) 1 மதிய உணவு வகையினைத் தேர்ந்தெடுக்க 9 வழிகளும் உள்ளது என்பதாகும். 

ஆகவே, உணவகத்தில் 1 சிற்றுண்டி உணவையோ அல்லது 1 மதிய உணவையோ சாப்பிட தேர்ந்தெடுப்பதற்கு 16 (7 சிற்றுண்டி வகைகள் + 9 மதிய உணவு வகைகள்) வெவ்வேறு விதமான வழிகள் உள்ளன 

2. எண்ணுதலில் பெருக்கல் கொள்கை

ஒன்றையொன்று சார்ந்து அமையும் இரண்டு செயல்பாடுகள் முறையே m வழிகளில் மற்றும் n வழிகளில் செயல்பட முடியும் எனில், பிறகு அந்த இரண்டு செயல்பாடுகளும் இணைந்து (m × n ) வழிகளில் செயல்பட முடியும்.

பின்வரும் சூழ்நிலை எண்ணுவதில் பெருக்கல் கொள்கையினைப் பற்றிப் நாம் மேலும் நன்கு புரிந்துகொள்ளலாம். 

சூழ்நிலை: 

கீழே கொடுக்கப்பட்டுள்ள படம் 7.3இல் உள்ளவாறு, ஒரு நகரில் A, B மற்றும் C என்ற மூன்று இடங்கள் உள்ளன. A இலிருந்து B இக்கு al, a2 மற்றும் a3 ஆகிய மூன்று பாதைகளும், B இலிருந்து C இக்கு b1 மற்றும் b2 என இரண்டு பாதைகளும் உள்ளன எனில், ஒருவர் A இலிருந்து C இக்கு B வழியாக எத்தனை வழிகளில் சென்றடைய இயலும் என்பதைக் காணலாம். 

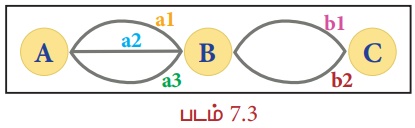
(i) முதலில் A இலிருந்து B இக்கு al, a2 மற்றும் a3 என 3 வெவ்வேறு வழிகளில் சென்றடைய முடியும்.

(ii) இரண்டாவதாக B இலிருந்து C இக்கு b1 மற்றும் b2 என 2 வெவ்வேறு வழிகளில் சென்றடைய முடியும்.

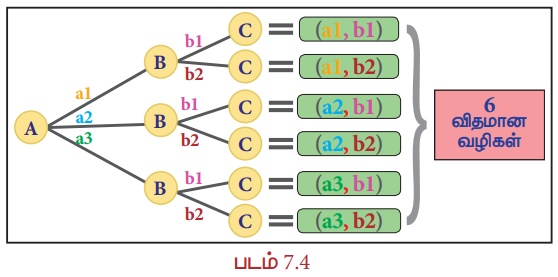
எனவே, படம் 7.4 இல் விளக்கிக் காட்டப்பட்டுள்ளதுப் போல் மொத்தம் 6( 3 × 2) வெவ்வேறு விதமான வழிகளில் செல்ல முடியும்.

இதிலிருந்து நாம் அறிந்து கொள்வது, A எனும் ஒரு செயல் m வழிகளிலும், B எனும் மற்றொரு செயல் n வழிகளிலும் செயல்படுகிறது, மேலும் இந்த இரண்டு செயல்களும் ஒன்றையொன்று சார்ந்துள்ளது எனில், செயல் A மற்றும் செயல் B ஆனது(m × n) வழிகளில் செயல்படும் என்பதாகும். பின்வரும் எடுத்துக்காட்டுகள் மூலம் இதனை மேலும் நன்கு புரிந்துகொள்ளலாம்.

எடுத்துக்காட்டு 7.2

பிரவீன் தனது பிறந்த நாளுக்காக படம் 7.5 இல் காட்டியுள்ளபடி 3 மேல் சட்டைகள், 2 முழுக்கால் சட்டைகள் மற்றும் 3 ஜோடி காலணிகள் வாங்கினான். அவன் தன்னுடைய பிறந்த நாளன்று எத்தனை விதமான வழிகளில் தான் வாங்கிய புதிய உடைமைகளை அணிந்துக் கொள்வதற்கு வாய்ப்புகள் உள்ளது?

தீர்வு:

பிரவீனிடத்தில் 3 மேல் சட்டைகள் 2 முழுக்கால் சட்டைகள் மற்றும் 3 ஜோடி  காலணிகள் உள்ளன பிரவீன் பிறந்த நாளன்று, இப்படியும் ஆடை அணியலாம். அல்லது கீழேபடம் 7.6இல் காட்டியுள்ளதுப் போலவும் ஆடை அணியலாம் 

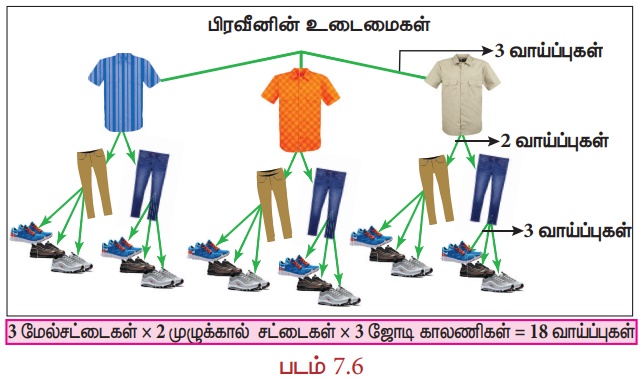
ஆக, பிரவீனுக்கு 18 (3 × 2 × 3) வெவ்வேறு விதங்களில் பிறந்தநாள் உடைமைகளை அணிந்துக் கொள்வதற்கான வாய்ப்புகள் உள்ளது.

எடுத்துக்காட்டு 7.3

எட்டாம் வகுப்பில் உள்ள ஒரு கணித மன்றத்தில் M, A, T மற்றும் H என்ற 4 உறுப்பினர்கள் உள்ளனர் எனில், கீழ்வரும் வினாக்களுக்கு விடையளிக்கவும்.

(i) கணித மன்றத் தலைவரைத் தேர்ந்தெடுப்பதற்கான வாய்ப்புகள் யாவை? 

(ii) கணித மன்றத் தலைவர் மற்றும் உபதலைவரைத் தேர்ந்தெடுப்பதற்கான வாய்ப்புகள் யாவை?

தீர்வு: 

(i) கணித மன்றத் தலைவரைத் தேர்ந்தெடுப்பதற்கான வாய்ப்புகள்

எட்டாம் வகுப்பில் உள்ள ஒரு கணித மன்றத்தில் M, A, T மற்றும் H என்ற 4 உறுப்பினர்கள் உள்ளனர் என்பதால் அவர்களில் ஒருவரை குழுத்தலைவராகத் தேர்ந்தெடுப்பதற்கு 4 (4 × 1) வாய்ப்புகள் உள்ளது.

(ii) கணித மன்றத் தலைவர் மற்றும் உபதலைவரைத் தேர்ந்தெடுப்பதற்கான வாய்ப்புகள் 

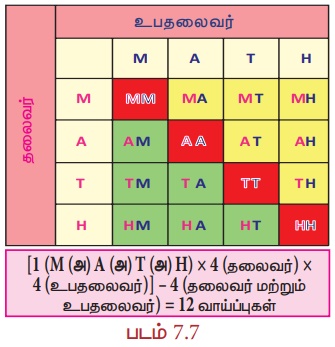
குழுத்தலைவர் மற்றும் உபதலைவரைத் தேர்ந்தெடுப்பதற்கான வாய்ப்புகளை நாம் படம் 7.7−இல் குறித்துள்ளவாறு அட்டவணைப்படுத்த வேண்டும். இந்த அட்டவணையில் சிவப்பு வண்ணத்தில் வண்ணமிடப்பட்டுள்ள கட்டங்களின்படி ஒருவரேத் தலைவர் மற்றும் உபதலைவர் என இரு பதவிகளையும் வகிக்க இயலாது. எனவே, சிவப்பு வண்ணமிடப்பட்டுள்ள கட்டங்களைத் தவிர்த்துக் கணக்கிட்டால், பச்சை வண்ணமிட்ட கட்டங்களின்படியோ அல்லது மஞ்சள் வண்ணமிட்ட கட்டங்களின்படியோ குழுத்தலைவர் மற்றும் உபதலைவரைத் தேர்ந்தெடுப்பதற்கு 12 ((4 × 4) − 4) 4 வெவ்வேறு விதமான வாய்ப்புகள் உள்ளன.

செயல்பாடு

1. 3 மற்றும் 5 என்ற எண்களைப் பயன்படுத்தி அமையக்கூடிய ஈரிலக்க எண்களை எழுதுக. (இலக்கங்களை மறுமுறையும் பயன்படுத்தலாம்).

செயல்பாடு இரண்டு பகுதிகளைக் கொண்டது.

(i) ஒன்றாம் இலக்கத்தைத் தெரிவுச் செய்தல் 

(ii) பத்தாம் இலக்கத்தைத் தெரிவுச் செய்தல்

கொடுக்கப்பட்டுள்ள அட்டவணையினை நிரப்புக.

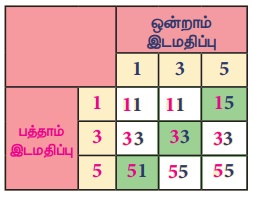
2. 1, 3 மற்றும் 5 என்ற எண்களைப் பயன்படுத்தி அமைக்கக் கூடிய மூவிலக்க எண்களைக் கண்டுபிடிக்கக் கீழே கொடுக்கப்பட்டுள்ள மரவுரு வரைப்படத்தைப் பூர்த்திச் செய்க (இலக்கங்களை மறுமுறைப் பயன்படுத்தக் கூடாது).

உங்களுக்குத் தெரியுமா?

6 உருக்கள் கொண்ட ஒரு கடவுச்சொல்லில் (password) முதல் இரு உருக்கள் ஒவ்வொன்றும் 26 ஆங்கில எழுத்துக்களில் ஏதேனும் ஒரு எழுத்தாகவும், மூன்றாவது உரு @, # , $ , % , & , _ , + , ~ , * அல்லது − என்ற 10 சிறப்பு உருக்களில் ஏதேனும் ஒன்றாகவும் மற்றும் அடுத்து வரும் 3 உருக்கள் ஒவ்வொன்றும் 0 முதல் 9 வரையிலான எண்களாகவும் அமைந்துள்ளது எனில் அத் தனித்துவமான ஒரு கடவுச்சொல்லை உருவாக்க மொத்தம் 26 × 26 × 10 × 10 × 10 × 10 = 67,60,000 விதமான வெவ்வேறு வாய்ப்புகள் உள்ளன.

எடுத்துக்காட்டு 7.4

சரியா, தவறா என விடையளிக்கும் 3 வினாக்கள்  அடங்கிய சிறுத்தேர்வில் ஒரு மாணவர் மொத்தம் எத்தனை வழிகளில் விடையளிக்க முடியும்?

தீர்வு: 

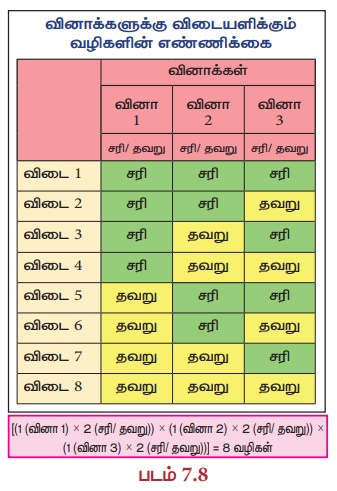
(i) படம் 7.8 இல் காட்டியுள்ளது போல் மாணவர்கள் முதல் வினாவிற்கு சரி என விடையளிக்கிறார்கள் என்று எடுத்துக் கொண்டால், இரண்டாவது மற்றும் மூன்றாவது வினாக்களுக்கு (சரி, சரி ) , ( சரி, தவறு), (தவறு , சரி ) மற்றும் (தவறு , தவறு ) போன்ற 4 விதங்களில் விடையளிக்க வாய்ப்புகள் உள்ளது.

(ii)  அதே போல்  மாணவர்கள் முதல் வினாவிற்கு தவறு என விடையளிக்கிறார்கள் என்று எடுத்துக் கொண்டால், இரண்டாவது மற்றும் மூன்றாவது வினாக்களுக்கு (சரி, சரி ) , ( சரி, தவறு), (தவறு , சரி ) மற்றும் (தவறு , தவறு ) போன்ற 4 விதங்களில் விடையளிக்க வாய்ப்புகள் உள்ளது.

ஆக, ஒவ்வொறு வினாவிற்கும் சரி அல்லது தவறு என்ற இரு வாய்ப்புகள் உள்ளதால் 3 சரியா, தவறா வினாக்களுக்கு மாணவர்கள் 8 (2 × 2 × 2 ) வெவ்வேறு விதமான வழிகளில் விடையளிக்க முடியும்.

எடுத்துக்காட்டு 7.5

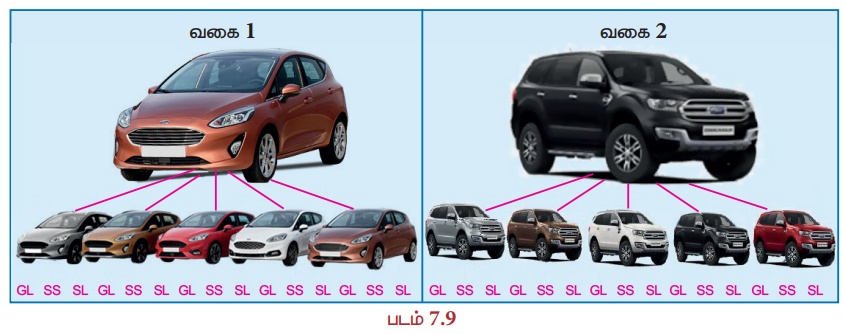
மதன் ஒரு மகிழுந்து (car) வாங்க விரும்புகிறார். அவருக்குக் கீழ்க்கண்டத் தெரிவுகள் (choice) உள்ளன. படம் 7.9−இல் கொடுக்கப்பட்டுள்ளது போன்று இரண்டு வகையான மகிழுந்துகள் இருப்பில் உள்ளது.

• ஒவ்வொறு வகையிலும் 5 வண்ணங்கள் கொண்ட மகிழுந்துகள் இருப்பில் உள்ளது.

• ஒவ்வொறு வகையிலும் 

(i) GL ( நிலையான  இரகம் )

(ii) SS ( விளையாட்டு  இரகம் )

(iii) SL ( சொகுசு  இரகம் ) என 3 விதமான இரகத்தில் மகிழுந்துகள் இருப்பில் உள்ளது.

(i) கொடுக்கப்பட்டுள்ள வாய்ப்புகளிலிருந்து ஏதேனும் ஒரு மகிழுந்தினை மதன் வாங்குவதற்கு எத்தனை விதமான வழிகள் உள்ளது? 

(ii) இரண்டாவது வகை மகிழுந்தில் வெள்ளை வண்ண மகிழுந்து இல்லையென்ற நிலையில், பிறவாய்ப்புகளிலிருந்து ஏதேனும் ஒரு மகிழுந்தினை மதன் வாங்குவதற்கு எத்தனை விதமான வழிகள் உள்ளது?

தீர்வு: 

(i) கொடுக்கப்பட்டுள்ள வாய்ப்புகளிலிருந்து ஏதேனும் ஒரு மகிழுந்தினை மதன் வாங்குவதற்கான வழிகள்

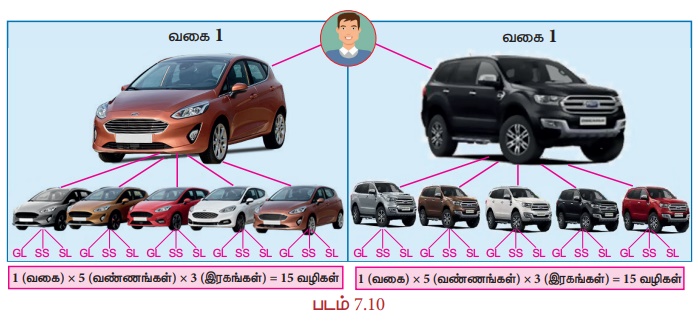
இங்கு 2 வகையான மகிழுந்துகளும், ஒவ்வொரு வகையில் 5 வண்ணங்களும், ஒவ்வொரு வகையில் 3 இரகங்களும் உள்ளது. எனவே, ஒரு மகிழுந்து வாங்குவதற்கு மொத்தமாக மதனுக்கு 30 [2 (1 × 5 × 3)] வெவ்வேறு விதமான வழிகள் உள்ளன. 

(ii) இரண்டாவது வகை மகிழுந்தில் வெள்ளை வண்ண மகிழுந்து இல்லையென்ற நிலையில்.

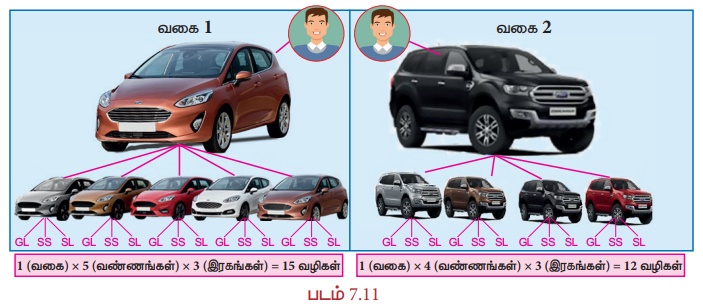
(i) முதல் வகையில், 5 வண்ணங்களும், 3 இரகங்களும் வாங்குவதற்கு வாய்ப்புகள் உள்ளபடியால் மொத்தமாக 15 (1 × 5 × 3) வெவ்வேறு விதமான வழிகளும்,

(ii) இரண்டாவது வகையில் 4 வண்ணங்களும், 3 இரகங்களும் வாங்குவதற்கு வாய்ப்புகள் உள்ளபடியால் மொத்தமாக 12 (1 × 4 × 3) வெவ்வேறு விதமான வழிகளும் உள்ளன.

ஆக, இங்கு ஒரு மகிழுந்து வாங்குவதற்கு மொத்தமாக மதனுக்கு 27 (15 + 12) வெவ்வேறு விதமான வழிகள் உள்ளன.

மேற்கண்ட எடுத்துக்காட்டு எண்ணுதலில் கூட்டல் மற்றும் பெருக்கல் விதிகளை விளக்குவதாக உள்ளது.