கணச் செயல்பாடுகள் (Set Operations)

கணச் செயல்பாடுகள் (Set Operations)

எண்களில் துவங்கி, வெகு விரைவாகவே எண்கணிதச் செயல்பாடுகளையும் கற்றுத் தேர்ந்தோம். இயற்கணிதத்தில் கோவைகளைக் கற்றவுடன் அவற்றைக் கூட்டவும், பெருக்கவும், (x²+2), (x−3) என எழுதவும், கற்றுத் தேர்ந்தோம். தற்போது கணங்களைப் பற்றி அறிந்தவுடன், இயல்பாகவே நம் மனதில் சில கேள்விகள் எழும். கணங்களை வைத்து என்ன செய்யலாம்? அவற்றை எச்செயல்பாடுகளில் பயன்படுத்தலாம்? எனப் பலவாறு சிந்தனைகள் எழலாம்.

இரண்டு அல்லது அதற்கு மேற்பட்ட கணங்களைக் குறிப்பிட்ட வரையறை அடிப்படையில் ஒரே கணமாக்குக. பின்னர் கணச் செயல்பாடுகளை மேற்கொள்க. வென்படத்தைப் பயன்படுத்தி கணங்களுக்கும் அவற்றின் மீது மேற்கொள்ளப்படும் செயல்பாடுகளுக்கும் உள்ள தொடர்பை காட்சிப்படுத்தலாம்.

ஜான் வென் ஓர் ஆங்கிலேயக் கணிதவியலாளர் ஆவார். இவர் கணங்களுக்கு இடையேயான உறவுகளைப் படங்களின் மூலம் விளக்கும் வென்படங்களை உருவாக்கினார். வென்படங்களானது கணக் கோட்பாடு, நிகழ்தகவு, புள்ளியியல், தர்க்கம் மற்றும் கணிப்பொறி அறிவியல் போன்ற துறைகளில் பயன்படுத்தப்படுகிறது.

1. நிரப்புக் கணம் (Complement of a Set)

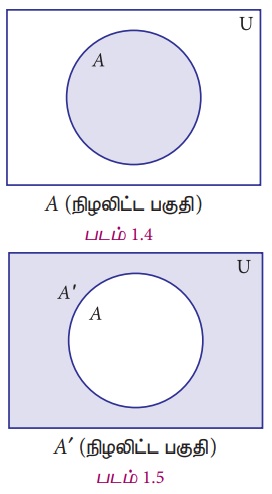
A என்ற கணத்தின் நிரப்புக் கணம் என்பது, கணம் A இன் உறுப்புகளைத் தவிர்த்து, அனைத்துக் கணத்தின் பிற எல்லா உறுப்புகளையும் கொண்ட கணம் ஆகும்.

நிரப்புக் கணத்தை A' அல்லது A^c எனக் குறிக்கலாம். A' = {x : x ∈ ∪, x ∉ A}

நிரப்புக் கணத்தின் வென்படம்

எடுத்துக்காட்டாக,

U = {வகுப்பில் உள்ள அனைத்து மாணவர்கள்} மற்றும் A = {வகுப்பில் உள்ள மட்டைப் பந்து விளையாடும் மாணவர்கள்} எனில் A' = {வகுப்பில் உள்ள மட்டைப் பந்து விளையாடாத மாணவர்கள்}|

எடுத்துக்காட்டு 1.10

U = {c, d, e, f, g, h, i, j} மற்றும் A = { c,d, g, j} எனில், A' காண்க.

தீர்வு

U = {c, d, e, f, g, h, i, j}, A = {c, d, g, j}

A' ={e, f, h, i}

குறிப்பு:

• (A')' = A

• ∪' = ∅

• ∅' = ∪

2. கணங்களின் சேர்ப்பு (Union of Two Sets)

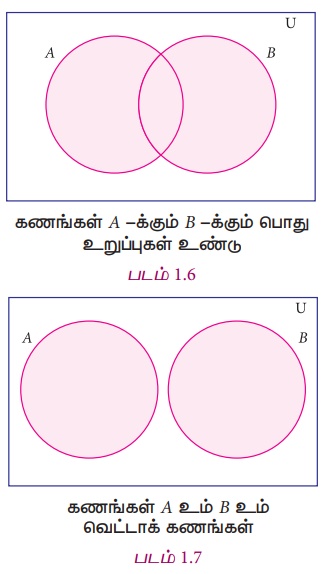
இரு கணங்கள் A மற்றும் B இன் சேர்ப்புக் கணம் என்பது, கணம் A அல்லது கணம் B அல்லது இரண்டிலும் உள்ள உறுப்புகளைக் கொண்ட கணம் ஆகும். இது A∪B எனக் குறிக்கப்படுகிறது. இதை A சேர்ப்பு B எனப் படிக்க வேண்டும்.

A∪B = {x : x ∈ A அல்ல து x ∈ B}

இரு கணங்களின் சேர்ப்பு − வென்படத்தில் குறித்தல்

எடுத்துக்காட்டாக,

P = {ஆசியா, ஆப்பிரிக்கா, அண்டார்டிகா, ஆஸ்திரேலியா} மற்றும்

Q = {ஐரோப்பா, வட அமெரிக்கா, தென் அமெரிக்கா} எனில் கணங்கள் P மற்றும் Q ஆகியவற்றின் சேர்ப்பு P∪Q = {ஆசியா, ஆப்பிரிக்கா, அண்டார்டிகா, ஆஸ்திரேலியா, ஐரோப்பா, வட அமெரிக்கா, தென் அமெரிக்கா} ஆகும்.

குறிப்பு:

 • A∪A = A

• A∪∅ = A

• A∪U = U இங்கு A என்பது அனைத்துக் கணம் U இன் உட்கணம்

• A⊆A∪B மற்றும் B⊆A∪B

• A∪B = B∪A (இரு கணங்களின் சேர்ப்பு பரிமாற்றத்தக்கது)

எடுத்துக்காட்டு 1.11

P={m, n} மற்றும் Q= {m, i, j} எனில், P மற்றும் Q என்ற கணங்களை வென் படத்தில் குறித்து, அதன் மூலம் P∪Q காண்க.

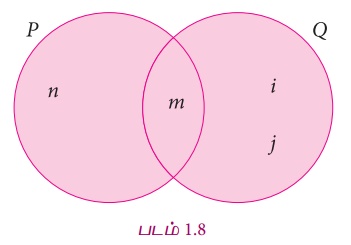
தீர்வு

P={m, n} மற்றும் Q= {m, i, j}

வென்படத்தில் இருந்து,

P∪Q={n, m, i,j}.

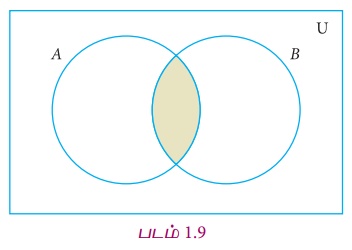
3. கணங்களில் வெட்டு (Intersection of Two Sets)

இரு கணங்கள் A மற்றும் B இன் வெட்டு என்பது அவ்விரு கணங்களின் பொது உறுப்புகளைக் கொண்ட கணமாகும். இதை A∩B எனக் குறிக்கிறோம். இதை A வெட்டு B எனப் படிக்கிறோம்.

A∩B={x: x ∈ A மற்றும் x ∈ B}

இரு கணங்களின் வெட்டு – வென்படத்தில் குறித்தல்

எடுத்துக்காட்டாக,

A = {1, 2, 6}; B = {2, 3, 4} எனில், A ∩ B = {2}. ஏனெனில், 2 ஆனது கணம் A மற்றும் B இன் பொது உறுப்பு.

குறிப்பு

• A∩A = A

• A∩∅ = ∅

• A∩U = A இங்கு A என்பது அனைத்துக்கணம் ∪−ன் உட்கணம்

• A∩B ⊆ A மற்றும் A∩B ⊆ B

• A∩B = B∩A (இரு கணங்களின் வெட்டுக்கணம் பரிமாற்று விதிக்கு உட்பட்டது)

எனவே, உண்மையில் n(A∪B) = n(A) + n(B) − n(A∩B).

இப்போது n(A∩B)= n(A) + n(B) − n(A∪B) எனச் சொல்வது எளிது. ஆகையால், n(A) மற்றும் n(B) கொடுக்கப்பட்டிருந்தால் வெட்டு மற்றும் சேர்ப்பு ஆகிய இரண்டிலொன்று தெரிந்தால் மற்றொன்றைத் தீர்மானிப்பது எளிது.

எடுத்துக்காட்டு 1.12

A = {x : x ஓர் இரட்டை இயல் எண் மற்றும் 1<x ≤ 12},

B = { x : x ஆனது 3 இன் மடங்கு, x ∈ ℕ மற்றும் x≤12} A∩B காண்க.

தீர்வு

A = {2, 4, 6, 8, 10, 12} மற்றும் B = {3, 6, 9, 12}

A∩B = {6, 12}

எடுத்துக்காட்டு 1.13

A = {2, 3} மற்றும் C = { } எனில், A∩C காண்க .

தீர்வு

இங்கு A மற்றும் C என்ற இரு கணங்களுக்கும் இடையே பொது உறுப்புகள் இல்லாததால் A∩C = { }

குறிப்பு

• B⊂A, எனில் A, B இன் சேர்ப்பு மற்றும் வெட்டு இவற்றை வென்படத்தில் காட்டுக.

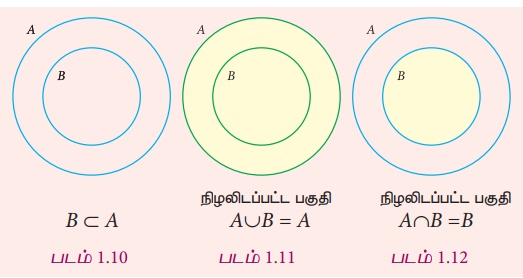
• A, B என்ற இரு கணங்களுக்கு A∪B = A∩B எனில் A = B

• n(A) = p மற்றும் n(B) = q என்க.

(அ) குறைந்தபட்சம் n(A∪B) = அதிகபட்சம் {p, q}

(ஆ) அதிகபட்சம் n(A∪B) = p + q

(இ) குறைந்தபட்சம் n(A∩B) = 0

(ஈ) அதிகபட்சம் n(A∩B) = குறைந்தபட்சம் {p, q}

4. கணங்களின் வித்தியாசம் (Difference of Two Sets)

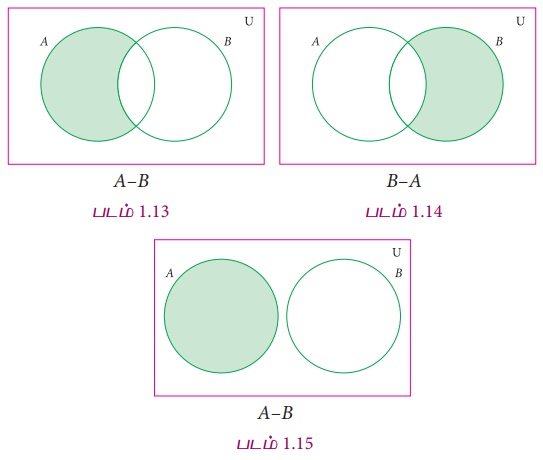
A, B என்பன இரு கணங்கள் என்க. கணம் A மற்றும் கணம் B இன் வித்தியாசம் என்பது கணம் A இல் உள்ள, ஆனால் கணம் B இல் இல்லா உறுப்புகளைக் கொண்ட கணமாகும். இதை A − B அல்லது A \ B என எழுதலாம். A − B என்பதை A வித்தியாசம் B எனப் படிக்க வேண்டும்.

  A−B = { x : x ∈ A மற்றும் x ∉ B}

  B−A = {y: y ∈ B மற்றும் y ∉ A}.

கண வித்தியாசங்களுக்கான வென்படங்கள்

எடுத்துக்காட்டு 1.14

A={−3,−2, 1, 4} மற்றும் B= {0, 1, 2, 4} எனில்,

(i) A−B

(ii) B−A ஐக் காண்க .

தீர்வு

A−B ={−3, −2, 1, 4} – {0, 1, 2, 4} = { −3, −2}

B−A = {0, 1, 2, 4} − {−3, −2, 1, 4} = { 0, 2}

குறிப்பு:

• A' = U − A

• A − B = A∩B'

• A − A = ∅

• A − ∅ = A

• A − B = B − A    <==> A=B

• A ∩ B = ∅ எனில்

A − B = A மற்றும் B−A=B

5. கணங்களின் சமச்சீர் வித்தியாசம் (Symmetric Difference of Sets)

A மற்றும் B என்ற கணங்களின் சமச்சீர் வித்தியாசம் என்பது (A−B) மற்றும் (B−A) இவற்றின் சேர்ப்பாகும். இது AΔB எனக் குறிப்பிடப்படுகிறது.

AΔB = (A−B) ∪ (B−A)

AΔB = { x : x ∈ A−B அல்லது x ∈ B−A}

எடுத்துக்காட்டு 1.15

A = {6, 7, 8, 9} மற்றும் B={8, 10, 12} எனில், AΔB காண்க .

தீர்வு

A−B = {6, 7, 9}

B−A = {10, 12}

AΔB = (A−B) ∪ (B−A) = {6, 7, 9} ∪{10,12}

AΔB = {6, 7, 9, 10, 12}.

சிந்தனைக் களம்: (A−B) ∩ (B−A) என்பது என்ன?

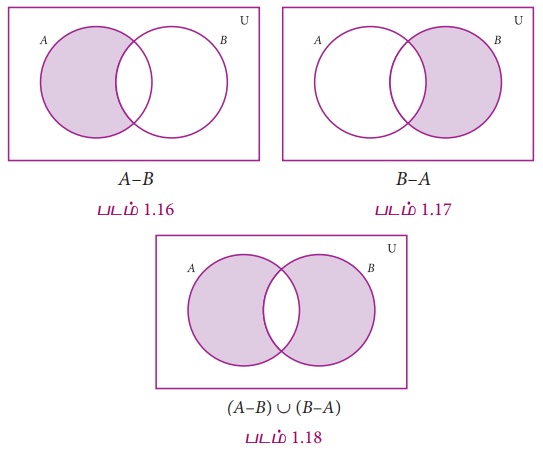
எடுத்துக்காட்டு 1.16

AΔB ஐ வென்படம் மூலம் வரைக.

தீர்வு

AΔB= (A−B) ∪ (B−A)

குறிப்பு:

• AΔA=∅

• AΔB = BΔA

• AΔB={x : x ∈ A∪B மற்றும் x ∉ A∩B}

• AΔB= (A∪B) − (A∩B)

எடுத்துக்காட்டு 1.17

அருகில் உள்ள படத்தில் இருந்து பின்வருவனவற்றைக் காண்க

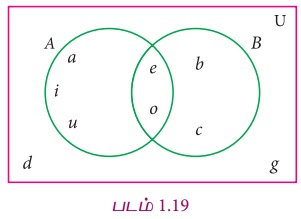
(i) A (ii) B (iii) A−B (iv) B−A (v) A' (vi) B' (vii)U

தீர்வு

(i) A = {a, e, i, o, u}

(ii) B = {b, c, e, o}

(iii) A−B= {a, i, u}

(iv) B−A = {b, c}

(v) A' = {b, c, d, g}

(vi) B' = {a, d, g, i, u}

(vii) U = {a, b, c,d,e, g, i, o, u}

எடுத்துக்காட்டு 1.18

வென்படம் வரைந்து, பின்வரும் கணச் செயல்களை வென்படத்தில் குறிக்கவும்.

(i) A' (ii) (A−B)' (iii) (A∪B)'

தீர்வு

(i) A'

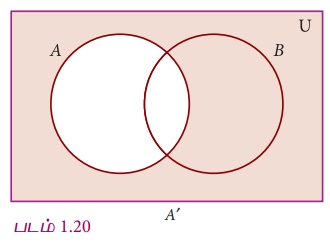
(ii) (A−B)'

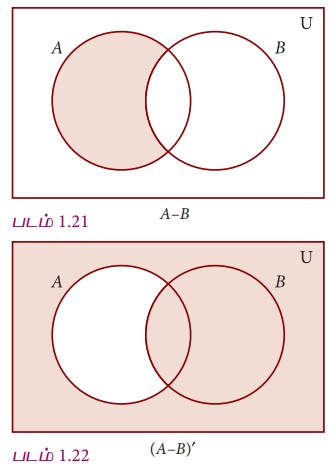
(iii) (A∪B)'