இயற்கணிதம் | இரண்டாம் பருவம் அலகு 3 | 7ஆம் வகுப்பு கணக்கு - பாடச்சுருக்கம் | 7th Maths : Term 2 Unit 3 : Algebra
7ஆம் வகுப்பு கணக்கு : இரண்டாம் பருவம் அலகு 3 : இயற்கணிதம்
பாடச்சுருக்கம்
உங்களுக்குத் தெரியுமா?
கணிதமேதை சீனிவாச இராமானுஜன் குறித்து நன்கறிவோம். அவரது குழந்தைப் பருவத்தில், அடுக்குகளைப் பயன்படுத்தி, பல அழகிய சமன்பாடுகளை உருவாக்கியிருக்கிறார். அவரது புகழ்பேசும் 'நோட்டுப் புத்தகங்கள்' இலிருந்து (Notebooks) ஓர் அற்புதமான அடுக்கு வடிவச் சமன்பாடு பின்வருமாறு:

22 × 66 × 11 × 11 = 33 × 33 × 44
ஒவ்வொரு காரணியிலும் அடிமானமும் அடுக்கும் ஒரே எண்ணாக இருப்பதைக் காண்க. மேலும், அடிமானத்தின் (அல்லது அடுக்குகளின்) கூடுதல் இருபுறமும் சமமாக உள்ளது. (அதாவது, 2+6+1+1=3+3+4=10). இதனை, அடுக்கு விதிகளைப் பயன்படுத்தி எளிதாக நிறுவலாம்.
இடப்பக்கம் = 22×66 ×11 ×11 = 22×66×1= 22 × (2×3)6
= 22 × 26 × 36 [ஏனெனில், (a×b)m = am × bm]
= 22+6 × 33+3 [ஏனெனில், am ×an = am+n]
= 28 × 33×33
= (22×4 × 33 ×33 [ஏனெனில், am×n = (am)n]
= 44 × 33 × 33 = 33 × 33 × 44
= வலப்பக்கம்.
இதேபோல், பின்வரும் அவரது பிற சமன்பாடுகளையும் நிறுவ முயற்சிக்கலாம்:
88 × 99 × 11 = 33 × 33 × 1212 (அடிமானத்தின் கூடுதல் 18)
44 × 2020 × 3030 × 11 = 66 × 2424 × 2525 (அடிமானத்தின் கூடுதல் 55)
பாடச்சுருக்கம்
• 'a' என்பது ஏதேனும் ஒரு முழுக்கள் எனில், a×a×a×...×a (n முறைகள்) = an ஆகும்.
இங்கு, a என்பது அடிமானம்; n என்பது அடுக்கு ஆகும்.
• 
• 'a' என்னும் எண், அதே எண்ணுடன் பெருக்கப்படும்போது, அந்தப் பெருக்கற்பலன் 'வர்க்கம்' எனப்படும். அது a2 எனக் குறிக்கப்படும். இதேபோல், அந்த வர்க்க எண் a2-ஐ, 'a' உடன் பெருக்கும்போது, அந்தப் பெருக்கற்பலன் 'கனம்' என்று அழைக்கப்படும். அது a3 எனக் குறிக்கப்படும்.
'a' மற்றும் ‘b' என்பன ஏதேனும் இரு பூச்சியமற்ற எண்கள் எனவும், ‘m' மற்றும் 'n' என்பன இயல் எண்கள் எனவும் கருதினால்,
(i) am × an = am+n (பெருக்கல் விதி)
(ii) am ÷ an = am-n, m>n (வகுத்தல் விதி)
(iii) (am)n = am×n (அடுக்கின் அடுக்கு விதி)
(iv) (a×b)m =am × bm
(v) (a/b)m=am/bm
• 0, 1, 5 மற்றும் 6 ஆகிய எண்களை ஒன்றாம் இலக்கமாகக் கொண்ட அடிமானத்தின் அடுக்கு எண்களின் விரிவின் ஒன்றாம் இலக்கம் அதே எண்களாக இருக்கும். எந்த ஒரு மிகை அடுக்கு உள்ள எண்ணுக்கும் இது பொருந்தும்.
• அடிமானம் 4இல் முடியும் அடுக்கு எண்களின் விரிவின் ஒன்றாம் இலக்கம், அதன் அடுக்கு ஒற்றை எண் ஆக இருக்கும்போது 4 ஆகவும், இரட்டை எண் ஆக இருக்கும்போது 6 ஆகவும் இருக்கும். இதேபோல், அடிமானம் 9 இல் முடியும் எண்களுக்கு, ஒற்றை எண் அடுக்குகளுக்கு ஒன்றாம் இலக்க எண் 9 ஆகவும், இரட்டை எண் அடுக்குகளுக்கு 1 ஆகவும் உள்ளது.
• ஓர் இயற்கணிதக் கோவையின் உறுப்புகளில் மாறிகளின் அதிகபட்ச அடுக்குகளை, அக்கோவையின் ‘படி' எனப்படும். ஒன்றுக்கு மேற்பட்ட மாறிகளைக் கொண்டிருந்தால், ஒவ்வோர் உறுப்பிலும் உள்ள மாறிகளின் அடுக்குகளைக் கூட்டி, அவற்றுள் அதிகபட்சக் கூடுதல், அக்கோவையின் படியாகக் கருதப்படும்.
இணையச் செயல்பாடு
செயல்பாட்டின் இறுதியில் கிடைக்கப் பெறுவது
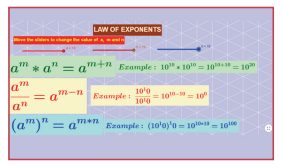
படி-1:
கீழ்க்காணும் உரலி/விரைவுக் குறியீட்டைப் பயன்படுத்தி ஜியோ ஜீப்ரா இணையப் பக்கத்தில் 'இயற்கணிதம்' என்னும் பணித்தாளிற்குச் செல்லவும். "அடுக்குகளின் விதி" என்ற பெயரில் பணித்தாள் உள்ளது.
படி-2 :
a, m மற்றும் n என்ற நழுவலை நகர்த்தி, முடிவுகளை உற்றுநோக்குக மற்றும் விதிகளைப் பயிற்சி செய்க.
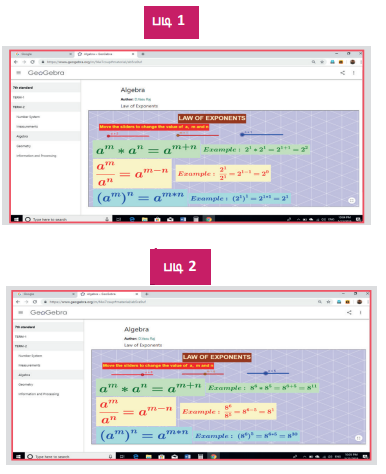
செயல்பாட்டிற்கான உரலி
இயற்கணிதம் : https://www.geogebra.org/m/f4w7csup#material/ab5ras9uf
அல்லது விரைவுக் குறியீட்டை ஸ்கேன் செய்க.