தனிநிலை சமவாய்ப்பு மாறிகள் (Discrete random variables)

1. தனிநிலை சமவாய்ப்பு மாறிகள் (Discrete random variables)

 இப்பாடப்பகுதியில் நாம் பின்வருவனவற்றைப் பற்றி விவாதிக்கலாம். 

(i) தனிநிலை சமவாய்ப்பு மாறி

 (ii) நிகழ்தகவு நிறைச் சார்பு.

(iii) குவிவு பரவல் சார்பு. 

(iv) நிகழ்தகவு நிறைச் சார்பிலிருந்து குவிவு பரவல் சார்பு பெறுதல்.

(v) குவிவு பரவல் சார்பிலிருந்து நிகழ்தகவு நிறைச் சார்பு பெறுதல்.

சமவாய்ப்பு மாறியின் வீச்சு கணமானது எண்களின் தனிநிலை கணம் எனில் சமவாய்ப்பு மாறியின் நேர்மாறு பிம்பம் முடிவுறு அல்லது எண்ணிடத்தக்க முடிவுறு கணமாக அமையும். அத்தகைய சமவாய்ப்பு மாறிகள் தனிநிலை சமவாய்ப்பு மாறிகள் என அழைக்கப்படுகின்றன. தனிநிலை கூறுவெளியில் வரையறுக்கப்படும் ஒரு சமவாய்ப்பு மாறி தனிநிலையாக இருக்கும்.

வரையறை 11.2 (தனிநிலை சமவாய்ப்பு மாறி)

கூறுவெளி S-லிருந்து மெய்யெண்கள் ℝ -க்கு வரையறுக்கப்படும் X எனும் ஒரு சமவாய்ப்பு மாறி, X -இன் வீச்சு எண்ணிடதக்கதாக இருந்தால் தனிநிலை சமவாய்ப்பு மாறியாகும். அதாவது, முடிவுறு அல்லது எண்ணிடதக்க முடிவுறா எண் மதிப்புகளை மட்டுமே கொண்டிருக்கும். இங்கு S கணத்தில் உள்ள ஒவ்வொரு மதிப்பின் நிகழ்தகவும் மிகையெண் நிகழ்தகவுக் கொண்டதாகவும், நிகழ்தகவுகளின் மொத்த கூடுதல் ஒன்றாகவும் இருக்கும். 

குறிப்புரை

 தொடர் கூறுவெளியில் கூட தனிநிலை சமவாய்ப்பு மாறியை வரையறுக்க இயலும். சான்றாக,

 (i) தொடர் கூறுவெளி S = [0,1] -இல், அனைத்து w ∈ S -க்கு , X(w) = 10 என வரையறுக்கப்படும் சமவாய்ப்பு மாறி என்பது ஒரு தனிநிலை சமவாய்ப்பு மாறியாகும். 

(ii) தொடர் கூறுவெளி S =[0,20]-க்கு, வரையறுக்கப்படும் சமவாய்ப்பு மாறி

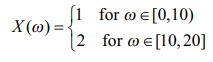
என்பது ஒரு தனிநிலை சமவாய்ப்பு மாறியாகும்.