அறிமுறை பரவல்கள் : சில சிறப்பு தனி நிலை பரவல்கள் (Theoretical Distributions: Some Special Discrete Distributions)

அறிமுறை பரவல்கள் : சில சிறப்பு தனி நிலை பரவல்கள் (Theoretical Distributions: Some Special Discrete Distributions)

 சராசரி மற்றும் பரவற்படியுடன் பலவேறு பொதுவான நிகழ்தகவு பரவல்களை முந்தையப் பகுதியில் கற்றோம். சில சிறப்பு வாய்ந்த தனிதிலை நிகழ்தகவு பரவல்களைக் காண்போம்.

இப்பகுதியில் பின்வரும் தனிநிலை பரவல்களைக் காண்போம்.

 (i) ஒரு புள்ளி பரவல்

(ii) இருபுள்ளி பரவல் 

(iii) பெர்னோலி பரவல்

(iv) ஈருறுப்பு பரவல்.

1. ஒரு புள்ளி பரவல் (The One point distribution)

f(x) = P(X = x0) = 1 என வரையறுக்கப்படும் நிகழ்தகவு நிறை சார்பு f (x) -ன்படி ஒரு புள்ளி x0 இருக்குமானால், சமவாய்ப்பு மாறி X -க்கு, ஒரு புள்ளி பரவற்படி அமையும்.

அதாவது ஒரு புள்ளியில் நிகழ்தகவு நிறை குவிந்துள்ளது.

குவிவு பரவல் சார்பு

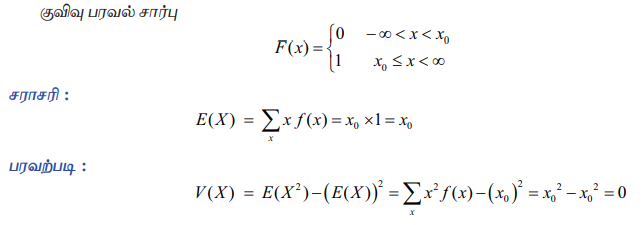
எனவே சராசரி மற்றும் பரவற்படி முறையே x0 மற்றும் 0 ஆகும்.

2. இரு புள்ளி பரவல் (The Two point distribution)

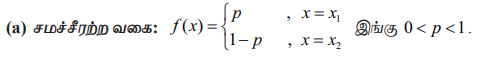
என அமையுமாறு இரு மதிப்புகள் x1 மற்றும் x2 இருக்குமானால் சமவாய்ப்பு மாறி X - க்கு இரு புள்ளி பரவல் உண்டு. 

குவிவு பரவல் சார்பு

3. பெர்னோலி பரவல் (The Bernoulli distribution)

வெற்றிக்கான நிகழ்தகவு p ஆக இருக்கும் சார்பற்ற சோதனைகளை முதலில் ஆராய்ந்தது சுவிஸ் கணிதவியலாளர் ஜேக்ஸ் பெர்னோலி (Jacques Bernoulli) (1654-1705) ஆவார். அவர் காலமாகி எட்டு ஆண்டுகளுக்குப் பிறகு 1713 இல் அவரது மருமகன் நிக்கோலஸால் வெளியிடப்பட்ட அவரது நூலான ஊகித்தல் கலையில், பெர்னோலி இதுபோன்ற சோதனைகளின் எண்ணிக்கை பெரிதாக இருந்தால், வெற்றிகளின் விகிதம் p க்கு நெருக்கமாக நிகழ்தகவு 1-க்கு அருகில் இருக்கும் எனச் சுட்டிக் காட்டினார்.

நிகழ்தகவு கருத்தியலில் சுவிஸ் கணிதவியலாளர் ஜேக்ஸ் பெர்னோலியின் பெயரால் விளங்கும் பெர்னோலி பரவல் ஒரு சமவாய்ப்பு மாறியின் தனிநிலை நிகழ்தகவு பரவலாகும். ஒன்றையொன்று விலக்கும் மற்றும் யாவுமளாவிய வகைகளில் அதாவது வெற்றி அல்லது தோல்வி ( எடுத்துக்காட்டாக: தலைகள் அல்லது பூக்கள், குறைபாடுள்ளவை அல்லது குறைபாடற்ற நல்ல பொருள்கள், பிறப்பு அல்லது இறப்பு அல்லது பல்வேறு சாத்திய ஜோடிகள்) என வகைப்படுத்தப்படும் ஒரு சமவாய்ப்பு சோதனை பெர்னோலி சோதனையாகும். சோதனைக்கு சோதனை மாறாது இருக்கும் வெற்றியின் நிகழ்தகவு அமையுமாறு பலமுறை சார்பற்ற வகையில் மேற்கொள்ளும் பெர்னோலி சோதனை மூலம் பெர்னோலி சோதனைத் தொடர் நேரிடுகிறது. 

வரையறை 11.10 (பெர்னோலி பரவல்)

X (வெற்றி) = 1 மற்றும் X (தோல்வி) = 0 என வரையறுக்கப்படும் ஒரு பெர்னோலி சோதனையுடன் இணைந்த சமவாய்ப்பு மாறி X -க்கு , 

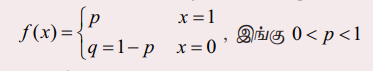
X என்பது பெர்னோலி சமவாய்ப்பு மாறி எனவும் மற்றும் f (x) என்பது பெர்னோலிபரவல் எனவும் முறையே அழைக்கப்படுகிறது

அல்லது சமானமாக

வெற்றி p ஆகிய நிகழ்தகவு உடைய பெர்னோலி பரவலை பின்பற்றும் ஒரு சமவாய்ப்பு மாறி, பண்பளவையாக அழைக்கப்பெறும p மற்றும் X ~ Ber(p) எனக் குறிப்பிடப்பட்டால், X - இன் நிகழ்தகவு நிறை சார்பு

f(x) = px( (1 – p)1-x   x = 0, 1 ஆகும்.

பெர்னோலி பரவலின் குவிவு பரவல்

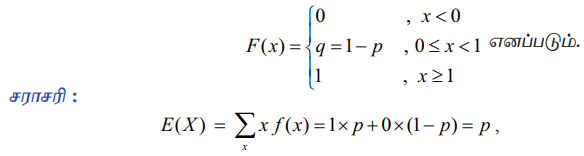
0 மற்றும் 1 மதிப்புகளை மட்டுமே X கொள்வதால் , அதன் எதிர்பார்ப்பு மதிப்பு p என்பதைப்'பார்த்ததில்லை எனக் கூறலாம். 

பரவற்படி :

V ( X ) = E ( X2 ) – (E ( X ))2 = ∑ x2 f (x ) p2

  = ( 12p + 02q) – p2 = p(1 – p ) = pq

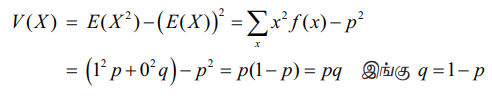
இங்கு q =1 - p

பண்பளவை p, சராசரி μ மற்றும் பரவற்படி σ 2 ஆகியவை உடைய பெர்னோலி பரவலைப் பின்பற்றும் X ஒரு பெர்னோலி சமவாய்ப்பு மாறி எனில்

 μ = p மற்றும் σ2 = pq 

p = q = 1/2 எனும்போது, பெர்னோலி பரவல்

ஆகும். சராசரி மற்றும் பரவற்படி முறையே ½ மற்றும் ¼  ஆகும்.

4. ஈருறுப்பு பரவல் (The Binomial Distribution)

தலைகள் அல்லது பூக்கள், வெற்றி அல்லது தோல்வி, குறைபாடு உடைய பொருள் அல்லது நல்ல பொருள் அல்லது இத்தகைய சாத்தியமான சோடிகள் இருக்கும் இரண்டு சாத்தியக் கூறுகளை மட்டுமே கொண்டிருக்கும் தொடர்ந்து நிகழ்த்தப்படும் சில சோதனைகளில் ஈருறுப்பு பரவல் முக்கியமாக பயன்படுத்தப்படுகிறது. அத்தகைய ஒவ்வொரு கூறுகளின் நிகழ்தகவினையும் பெருக்கல் விதியினைப் பயன்படுத்தி சில சமயங்களில் கிளை வரைபடத்துடன் கணிக்கப்படுகிறது.

ஒரு நாணயம் ஒரு முறை சுண்டப்படுகிறது என்க. தலைகளின் எண்ணிக்கையை X குறிக்கிறது என்க. இனி X ~ Ber(p), ஏனெனில் p அல்லது 1 – p எனும் நிகழ்தகவுடன் தலை (X =1) அல்லது பூ (X=0) இரண்டில் ஒன்று மட்டுமே கிடைக்கிறது. 

ஒரு நாணயம் n தடவை சுண்டப்படுகிறது என்க. தலைகளின் எண்ணிக்கையை X குறிக்கிறது என்க. இனி 0,1,2,...,n ஆகிய மதிப்புகளை X கொள்கிறது. தலைகளின் எண்ணிக்கை x -க்கான நிகழ்தகவு

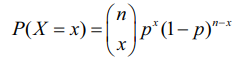
X = x, என்பது n சுண்டல்களில் x தலைகளின் சேர்ப்பிப்பிற்கு ஒத்ததாக, அதாவது(nx) வழிகளில் தலைகளும் மற்றும் மீதமுள்ள வழிகளில் n- x பூக்களும் என அமைகிறது. எனவே ஒவ்வொரு விளைவின் நிகழ்தகவு p x (1 − p)n−xஆகும். n மதிப்பு 30-க்கும் குறைவாக இருக்கும்போது ஈருறுப்பு தேற்றம் பயன்படுத்துவது பொருத்தமானதாகும்.

வரையறை 11.11 (ஈருறுப்பு சமவாய்ப்பு மாறி) 

n - தொடர்ச்சியான முயற்சிகளில் உள்ள வெற்றிகளின் எண்ணிக்கையை X குறித்தால், (i) n -தொடர்ச்சியான முயற்சிகள் சார்பற்றவையாகவும் மற்றும் n-எண்ணிடத்தக்கவையாகவும்

(ii) 'வெற்றி' அல்லது 'தோல்வி' எனப் பெயரிடப்பட்ட இரு சாத்தியமான விளைவுகளைமட்டுமே ஒவ்வொரு முயற்சியும் கொண்டிருக்கவும் 

(iii) ஒவ்வொரு முயற்சியிலும் p எனக் குறிக்கப்படும் வெற்றியின் நிகழ்தகவு மாறாதுஇருக்கவும், அமைந்தால் ஒரு தனிநிலை சமவாய்ப்பு மாறி X ஈருறுப்பு சமவாய்ப்பு மாறி என அழைக்கப்படும்.

வரையறை 11.12 (ஈருறுப்பு பரவல்)

ஈருறுப்பு சமவாய்ப்பு மாறி X என்பது n-சார்பற்ற முயற்சிகளில் வெற்றிகளின் எண்ணிக்கையைக் குறிக்கிறது என்க. வெற்றிக்கான நிகழ்தகவு p எனக் கொண்டால், தோல்விக்கான நிகழ்தகவு q =1 – p ஆகும். ஈருறுப்பு பரவலை X ~ B(n, p) எனக் குறிப்பர்.

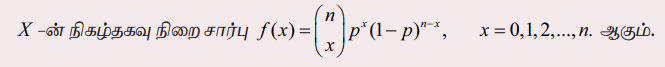
ஈருறுப்பு விரிவாக்கத்திலிருந்து பரவலின் பெயர் பெறப்பட்டது. a மற்றும் b, மாறிலிகளுக்கு, ஈருறுப்பு விரிவாக்கம்,

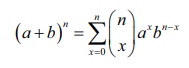ஆகும்.

ஒரு தனி முயற்சியில் வெற்றிக்கான நிகழ்தகவு p என்க. இனி, a = p மற்றும் b =1 – p என்பதைப் ஈருறுப்பு விரிவாக்கத்தில் பயன்படுத்தும்போது ஈருறுப்பு சமவாய்ப்பு மாறிகளின் நிகழ்தகவுகளின் கூடுதல் 1 எனக் காணலாம். சோதனையில் ஒவ்வொரு முயற்சியும் இரு விளைவுகள், {வெற்றி, தோல்வி} என வகைபடுத்துவதால், பரவல் "ஈர்"-உறுப்பு என அழைக்கப்படுகிறது.

p மற்றும் n எனும் பண்பளவைகளைக் கொண்ட ஈருறுப்புப் பரவலினைப் பின்பற்றும் ஓர் ஈருறுப்பு சமவாய்ப்பு மாறி X என்க. சராசரி μ மற்றும் பரவற்படி σ2 முறையே

μ = np and σ2 = np(1- p)

எதிர்பார்க்கப்படும் மதிப்பு பொதுவாக சமவாய்ப்பு மாறி கொள்ளும் மதிப்பாக இருக்காது. பன்முறை சார்பற்று செய்யப்படும் ஒரு சோதனையில் ஒரு சமவாய்ப்பு மாறியின் எதிர்பார்ப்பைப் புரிந்து கொள்ள இந்த எதிர்பார்க்கப்படும் மதிப்பு உதவும். p = 0.5 எனும்போது அல்லது n பெரியதாக இருக்கும் போது ஈருறுப்பு பரவலின் அமைப்பு சமச்சீராக அமையும்.

சராசரி மற்றும் பரவற்படி முறையே n/2 மற்றும் n/4ஆகும். 

எடுத்துக்காட்டு 11.19

பின்வருவனவற்றிற்கு ஈருறுப்பு பரவல் காணவும். 

(i) ஐந்து சீரான நாணயங்கள் ஒருமுறை சுண்டப்படுகின்றன மற்றும் தலைகளின் எண்ணிக்கையை X குறிக்கிறது என்க. 

(ii) ஒருசீரான பகடை 10 முறை உருட்டப்படுகிறது மற்றும் எண் 4 தோன்றுவதின் எண்ணிக்கையை X  குறிக்கிறது என்க. 

தீர்வு

 (i) ஐந்து சீரான நாணயங்கள் ஒருமுறை சுண்டப்படுகின்றன. நாணயங்கள் சீரானவை என்பதால்ஓர் ஒற்றை நாணயத்திலிருந்து ஒரு தலை கிடைப்பதற்கான நிகழ்தகவு p = (1/2)  மற்றும் q = 1 – p = (1/2)

ஐந்து நாணயங்களிலிருந்து தலைகள் கிடைப்பதற்கான எண்ணிக்கையை X குறிக்கிறது என்க. 0,1,2,3,4 மற்றும் 5 ஆகிய மதிப்புகளைக் கொள்ளும் ஈருறுப்பு சமவாய்ப்பு மாறி X என்க. n = 5 மற்றும் p = (1/2 ) ஆகும். அதாவது X ~ B( 5 1/2 ) ஆகும்.

எனவே ஈருறுப்பு பரவல்

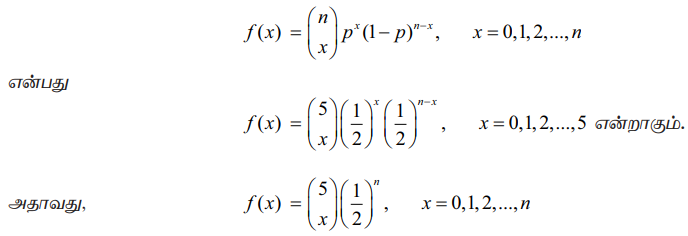
(ii) ஒரு சீரான பகடை 10 முறை உருட்டப்படுகிறது மற்றும் எண் 4 தோன்றுவதின் எண்ணிக்கையைX குறிக்கிறது என்க. 0, 1, 2, 3,... 10 எனும் மதிப்புகளைக் கொள்ளும் ஈருறுப்பு சமவாய்ப்புமாறி X என்க. n = 10 மற்றும் p = (1/6)  ஆகும். அதாவது X ~ B(10, 1/6) ஆகும்.

பகடையில் நான்கு கிடைப்பதற்கான நிகழ்தகவு p = 1/6 மற்றும் q =1 - p = 5/6 ஆகும்.

எனவே ஈருறுப்பு பரவல்

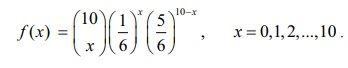
எடுத்துக்காட்டு 11.20

பத்து வினாக்கள் கொண்ட ஒரு பல்வாய்ப்புத் தேர்வில், ஒவ்வொரு வினாவிற்கும் நான்கு கவனச் சிதறல் விடைகளில் ஒன்று சரியான விடையாகும். ஊகத்தின் அடிப்படையில் ஒரு மாணவர் விடையளிக்கிறார் என்க. சரியான விடைகளின் எண்ணிக்கையை X குறிக்கிறது எனில், (i) ஈருறுப்பு பரவல் (ii) மாணவர் ஏழு சரியான விடைகள் அளிப்பதற்கான நிகழ்தகவு (iii) குறைந்தபட்சம் ஒரு விடை சரியானதாக இருக்க நிகழ்தகவு ஆகியவற்றைக் காண்க. 

தீர்வு

(i) வெற்றிகளின் எண்ணிக்கையை X குறிப்பதால், X கொள்ளும் மதிப்புகள் 0, 1, 2,..., 10 ஆகும். வெற்றிக்கான நிகழ்தகவு p = 1/4 மற்றும் தோல்விக்கு q =1 – p = 3/4 , மற்றும் n = 10 ஆகும். எனவே X ஈருறுப்பு பரவலை அனுசரிக்கிறது.

எடுத்துக்காட்டு 11.21

ஓர் ஈருறுப்பு மாறி X யின் சராசரி மற்றும் பரவற்படி முறையே 2 மற்றும் 1.5 ஆகும். காண்க

(i) P(X = 0) 

(ii) P(X = 1) 

(iii) P(X  ≥ 1) ஆகியவற்றைக் காண்க. 

தீர்வு

நிகழ்தகவு கண்டறிய n மற்றும் p ஆகிய பண்பளவைகளின் மதிப்புகளைக் கண்டறிய வேண்டும்.தரப்பட்ட தகவல்களிலிருந்து,

சராசரி = np = 2 மற்றும் பரவற்படி = npq =1.5 

இதிலிருந்து பெறுவது npq/np =1.5/2 = 3/4

q = 3/4 மற்றும் p = 1 - q = 1 – (3/4) = (1/4)

np = 2, என்பதன் மூலம் n = 2/p = 8. 

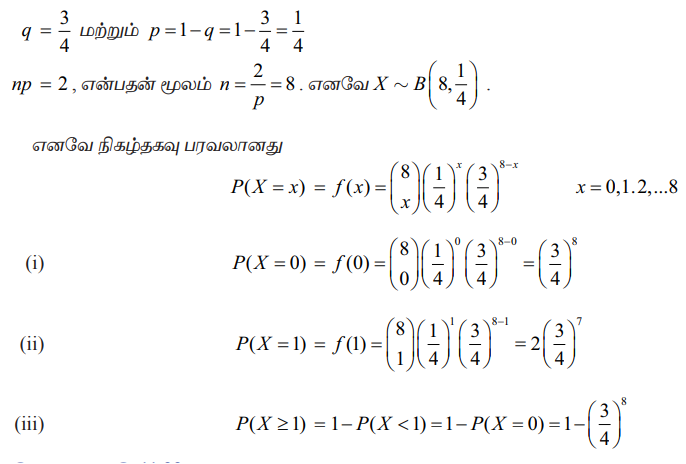
எடுத்துக்காட்டு 11.22

ABC குழுமம் தயாரிக்கும் பொருட்களில் சராசரியாக, 20% பொருட்கள் குறைபாடுள்ளவை எனக் கண்டறியப்பட்டது. சமவாய்ப்பு முறையில் இதிலிருந்து 6 பொருட்கள் தேர்ந்தெடுக்கப்படுகிறது. மேலும் குறைபாடுள்ள பொருட்களின் எண்ணிக்கையை X குறித்தால் (i) இரு பொருட்கள் குறைபாடுள்ளவை (ii) அதிகபட்சம் ஒரு பொருள் குறைபாடுள்ளது (iii) குறைந்தபட்சம் இரு பொருட்கள் குறைபாடுள்ளவை. ஆகியவற்றிற்கான நிகழ்தகவு காண்க. 

தீர்வு

கொடுக்கப்பட்டது n = 6.

 குறைபாடுள்ள ஒரு பொருளைத் தேர்ந்தெடுப்பதற்கான நிகழ்தகவு 20/100 அதாவது p = (1/5)

q = 1 – p = 4/5 குறைபாடுள்ள பொருட்களின் எண்ணிக்கையை X குறிப்பதால், X கொள்ளும் மதிப்புகள் 0, 1, 2,..., 6 ஆகும்.

எனவே X ஈருறுப்பு பரவலைப் பின்பற்றுகிறது. அதனைX~B(6,(1/5)) எனக் குறிப்பிடலாம்.