பாடச்சுருக்கம்

பாடச்சுருக்கம்

• ஒரு சமவாய்ப்பு மாறி X என்பது S எனும் கூறுவெளியிலிருந்து ℝ எனும் மெய்யெண் கணத்தின் மீது பின்வருமாறு வரையறுக்கப்படும் சார்பாகும். 

ℝ -இல் உள்ள இடைவெளி அல்லது உட்கணம் அல்லது கூறுபுள்ளிகளின் நேர்மாறு பிம்பங்கள்

S -இல், ஒரு நிகழ்வாக அமைகிறது. ஒவ்வொரு நிகழ்வும் நிகழ்தகவு மதிப்பைக் கொண்டிருக்கும். 

• கூறுவெளி S-லிருந்து மெய்யெண்கள் ℝ-க்கு வரையறுக்கப்படும் X எனும் ஒரு சமவாய்ப்பு மாறி, X -இன் வீச்சு எண்ணிடதக்கதாக இருந்தால் தனிநிலை சமவாய்ப்பு மாறியாகும். அதாவது, முடிவுறு அல்லது எண்ணிடதக்க முடிவுறா எண் மதிப்புகளை மட்டுமே கொண்டிருக்கும். இங்கு S கணத்தில் உள்ள ஒவ்வொரு மதிப்பின் நிகழ்தகவும் மிகையெண் நிகழ்தகவுக் கொண்டதாகவும், நிகழ்தகவுகளின் மொத்த கூடுதல் ஒன்றாகவும் இருக்கும். 

•  x1, x2, x3,... xn..., என்ற தனி மதிப்புகளைக் கொண்ட X என்பது ஒரு தனிநிலை சமவாய்ப்பு மாறியெனில், சார்பு f (.) அல்லது p(.) எனக் குறிப்பிடப்படுகிறது. மேலும் f(xk) = P(X = xk), k = 1,2,3,...n,... என்பது நிகழ்தகவு நிறைச் சார்பாக வரையறுக்கப்படுகிறது.

• x1 < x2 < x3 < … எனும்படி x1, x2, x3 …….. மதிப்புகளுக்கு F(x)-ஐ நிகழ்தகவு நிறைச் சார்பாகக் கொண்டிருக்கும் தனிநிலை சமவாய்ப்பு மாறி X -இன் குவிவு பரவல் சார்பு F(x)-இன் நிகழ்தகவு நிறைச் சார்பு F (x) = P(X ≤ x) = ∑xi≤x f (xi ), x ∈ ℝ ஆகும்.

• S என்பது ஒரு கூறுவெளி என்க. X: S → ℝ எனும் ஒரு சமவாய்ப்பு மாறி ℝ -ன் ஒரு கணமான I-ல் ஏதேனும் மதிப்பைப் பெறும என்க. I -இல் உள்ள அனைத்து x-க்கும் P(X = x) = 0 என்பது X -இன் ஒரு தொடர்ச்சியான சமவாய்ப்பு மாறியாகும். 

• தொடர்ச்சியான சமவாய்ப்பு மாறியில் x ∈  [a,b] எனுமாறு உள்ள சாத்தியமான ஒவ்வொரு நிகழ்வு x -ற்கும் P(a ≤ x ≤ b) = b∫a f (x) dx எனும் பண்பு உள்ளது எனில், f (x) எனும் ஒரு குறையற்ற மெய்யெண் மதிப்புடைய சார்பானது, நிகழ்தகவு அடர்த்தி சார்பாகும். 

• f(x) எனும் நிகழ்தகவு அடர்த்தியுடைய ஒரு தொடர்ச்சியான சமவாய்ப்பு மாறி X-ன் பரவல்சார்பு அல்லது குவிவு பரவல் சார்பு F(x) என்பது

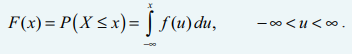
• ஒரு சமவாய்ப்பு மாறி X -இன் நிகழ்தகவு பரவல் சார்பு f (x) என்க. E(X) அல்லது – எனக்குறிப்பிடப்படும்

என்பது எதிர்பார்ப்பின் மதிப்பு அல்லது சராசரி அல்லது X -இன் கணித எதிர்பார்ப்பு என வரையறுக்கப்படுகிறது.

• V(X) or σ2 (or σx2) எனக் குறிப்பிடப்படும் சமவாய்ப்பு மாறி X-ன் பரவற்படி

V(X) = E(X – E(X))2 = E(X – μ)2 ஆகும். 

கணித எதிர்பார்ப்பு மற்றும் பரவற்படியின் பண்புகள்

(i) E(ax + b) = aE(X) + b , இங்கு a மற்றும் b ஆகியன மாறிலிகள்.

கிளைத்தேற்றம் 1 : E(ax) = aE(X) (b = 0 எனும்போது)

 கிளைத்தேற்றம் 2 : E(b) = b (a = 0 எனும்போது)

(ii) Var(X) = E(X2) – (E(X))2

 (iii) Var(aX + b) = a2Var(X) இங்குa மற்றும் b ஆகியவை மாறிலிகள்.

கிளைத்தேற்றம் 3 : V(aX ) = a2V(X)  (b = 0 எனும்போது)

கிளைத்தேற்றம் 4 : V(b) = 0 (a = 0 எனும்போது)

 • X (வெற்றி) = 1 மற்றும் X (தோல்வி) = 0 என வரையறுக்கப்படும் ஒரு பெர்னோலி சோதனையுடன் இணைந்த சமவாய்ப்பு மாறி X -க்கு

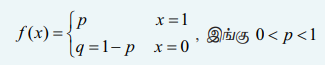
X என்பது பெர்னோலி சமவாய்ப்பு மாறி எனவும் மற்றும் f (x) என்பது பெர்னோலி பரவல் எனவும் முறையே அழைக்கப்படுகிறது

• X என்பது பெர்னோலி சமவாய்ப்பு மாறி எனவும் மற்றும் f (x) என்பது பெர்னோலி பரவல் எனவும்முறையே அழைக்கப்படுகிறது.

• பண்பளவை p உடைய பெர்னோலி பரவலைப் பின்பற்றும் X ஒரு பெர்னோலி சமவாய்ப்பு மாறி எனில், சராசரி μ மற்றும் பரவற்படி σ 2 ஆகியவை

 μ = p மற்றும்  σ2 = pq ஆகும். 

• n-தொடர்ச்சியான முயற்சிகளில் உள்ள வெற்றிகளின் எண்ணிக்கையை X குறித்தால்,

(i) n -தொடர்ச்சியான முயற்சிகள் சார்பற்றவையாகவும் மற்றும் n-எண்ணிடத்தக்கவையாகவும் 

(ii) 'வெற்றி' அல்லது 'தோல்வி' எனப் பெயரிடப்பட்ட இரு சாத்தியமான விளைவுகளைமட்டுமே ஒவ்வொரு முயற்சியும் கொண்டிருக்கவும் 

(iii) ஒவ்வொரு முயற்சியிலும் p எனக் குறிக்கப்படும் வெற்றியின் நிகழ்தகவு மாறாதுஇருக்கவும், அமைந்தால் ஒரு தனிநிலை சமவாய்ப்பு மாறி  X  ஈருறுப்பு சமவாய்ப்பு மாறி என அழைக்கப்படும்.

• ஈருறுப்பு சமவாய்ப்பு மாறி X என்பது n-சார்பற்ற முயற்சிகளில் வெற்றிகளின் எண்ணிக்கையைக் குறிக்கிறது என்க. வெற்றிக்கான நிகழ்தகவு p எனக் கொண்டால், தோல்விக்கான நிகழ்தகவு

q =1 – p ஆகும். ஈருறுப்பு பரவலை X ~ B(n, p) எனக் குறிப்பர்.

X -ன் நிகழ்தகவு நிறை சார்பு  f (x) =  px (1 − p)n− x , x = 0,1, 2,..., n. ஆகும்.

• p மற்றும் n எனும் பண்பளவைகளைக் கொண்ட ஓர் ஈருறுப்பு பரவலின் ஈருறுப்புசமவாய்ப்பு மாறி X என்க. சராசரி μ  மற்றும் பரவற்படி σ2  முறையே

μ = np மற்றும் σ2 = np(1 - p) ஆகும்.