நிகழ்தகவு பரவல்கள் | கணிதவியல் - குவிவு பரவல் சார்பிலிருந்து நிகழ்தகவு நிறை சார்பு (Probability Mass Function from Cumulative Distribution Function) | 12th Maths : UNIT 11 : Probability Distributions
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 11 : நிகழ்தகவு பரவல்கள்
குவிவு பரவல் சார்பிலிருந்து நிகழ்தகவு நிறை சார்பு (Probability Mass Function from Cumulative Distribution Function)
5. குவிவு பரவல் சார்பிலிருந்து நிகழ்தகவு நிறை சார்பு (Probability Mass Function from Cumulative Distribution Function)
ஒரு தனிநிலை சமவாய்ப்பு மாறி X-க்கு, குவிவு பரவல் சார்பு F ஒவ்வொரு xi -யிலும் துள்ளல் இருக்கும். மேலும் அடுத்தடுத்த xi -களில் மாறாமலும் இருக்கும். xi -இல் இருக்கும் துள்ளலின் உயரம் f (xi); இதே முறையில் F -லிருந்து xi -இன் நிகழ்தகவை மீட்டெடுக்கலாம்.
x1 < x2 ,< x3…… என்றவாறு இருக்கும் x1, x2 , x3…… மதிப்புகளைக் கொண்டிருக்கும் தனிநிலை சமவாய்ப்பு மாறி X என்க. மற்றும் F(xi) என்பது பரவல் சார்பாகும். எனவே நிகழ்தகவு நிறை சார்பு f (xi) ஆனது, -
f (xi) = F(xi)- F(xi-1), i =1,2,3,... ஆகும்.
குறிப்பு
x = a-ல் F(x) சார்பின் துள்ளல் |F ( a + ) − F ( a − )| ஆகும். F குறைவுறாமலும் மற்றும் வலப்பக்கமாக தொடர்ச்சியாகவும் இருப்பதால், குவிவு பரவல் சார்பு F-ன் துள்ளல் P(X = x) = F(x) - F(x− ) ஆகும்.
இங்கு துள்ளல் (தொடர்ச்சியில்லாமல் இருப்பதால்) நிகழ்தகவாக நிகழ்கிறது. அதாவது ஒரு குவிவு பரவல் சார்பின் தொடர்ச்சியற்றவைகளின் கணம் எண்ணத்தக்கது!
எடுத்துக்காட்டு 11.9
கீழே கொடுக்கப்பட்டுள்ள குவிவு பரவல் சார்பு F(x) -இன் தனிநிலை சமவாய்ப்பு மாறி X -யின் நிகழ்தகவு நிறைசார்பினைக் காண்க.
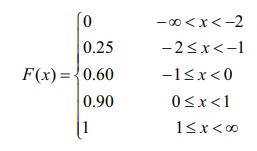
மேலும் (i) P(X < 0) மற்றும் (ii) P(X ≥ -1) காண்க
தீர்வு
'X என்பது ஒரு தனிநிலை சமவாய்ப்பு மாறி என்பதால், கொடுக்கப்பட்ட தகவல்களிலிருந்து, X பின்வரும் மதிப்புகளான -2,-1, 0 மற்றும் 1 ஆகியவற்றைப் பெறும.
வரையறைப்படி தனிநிலை சமவாய்ப்பு மாறி X-க்கு, f (x) = P(X = x)
எனவே F(x) -இன் x = -2-ல் இடப்பக்க எல்லை F(-2-) ஆகும்.
f(-2) = P(X = -2) = F(-2) - F(-2 ) = 0.25 - 0 = 0.25.
இதே போன்று ஏனைய துள்ளல் புள்ளிகளுக்கும்,
f(-1) = P(X = -1) = F(-1) - F(-2) = 0.60 - 0.25 = 0.35.
f(0) = P(X = 0) = F(0) - F(-1) = 0.90 - 0.60 = 0.30,
f (1) = P(X = 1) = F(1) - F(0) =1 - 0.90 = 0.10 எனப் பெறப்படுகிறது.
எனவே நிகழ்தகவு நிறை சார்பானது
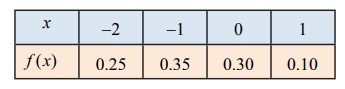
ஆகும்.
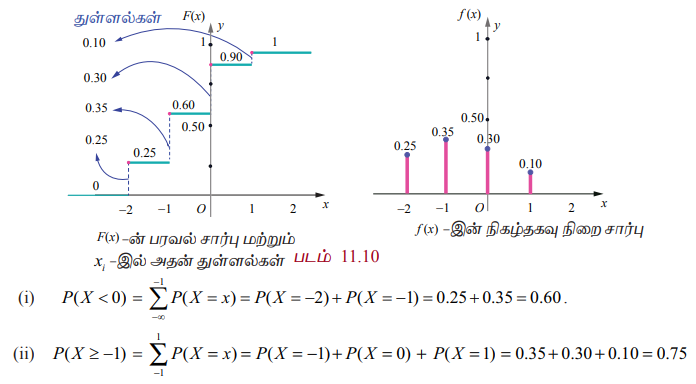
F(x) எனும் பரவல் சார்பிற்கு x = -2, -1, 0, மற்றும் 1-ல் துள்ளல்கள் உள்ளன. அந்த துள்ளல்கள் முறையே, 0.25, 0.35, 0.30, மற்றும் 0.1 என கீழ்க்காணும் படத்தில் காண்பிக்கப்பட்டுள்ளது.
இந்த துள்ளல்களே நிகழ்தகவு நிறைச் சார்பினைத் தீர்மானிக்கின்றன.
எடுத்துக்காட்டு 11.10
ஒரு தனிநிலை சார்பு X -ன் நிகழ்தகவு நிறை சார்பானது

எனில், (i) P(2 < X < 6) (ii) P(2 ≤ X < 5) (iii) P(X ≤ 4) (iv) P(3 < X) என்பவற்றைக் காண்க.
தீர்வு
கொடுக்கப்பட்ட சார்பு நிகழ்தகவு நிறை சார்பு என்பதால் மொத்த நிகழ்தகவு ஒன்றாகும். அதாவது ∑x f (x) = 1 ஆகும்.
கொடுக்கப்பட்ட தகவல்களிலிருந்து k + 2k + 6k + 5k + 6k + 10k = 1
30k = 1
⇒ k =1/30
எனவே நிகழ்தகவு நிறை சார்பானது,
