வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் - திசையிலிப் பெருக்கல் மற்றும் வெக்டர் பெருக்கல் (Scalar Product and Vector Product) | 12th Maths : UNIT 6 : Applications of Vector Algebra
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்
திசையிலிப் பெருக்கல் மற்றும் வெக்டர் பெருக்கல் (Scalar Product and Vector Product)
திசையிலிப் பெருக்கல் மற்றும் வெக்டர் பெருக்கல் (Scalar Product and Vector Product)
முன் வகுப்பில் கற்ற திசையிலிப் பெருக்கல் மற்றும் வெக்டர் பெருக்கல் ஆகியவற்றை நினைவுகூர்வோம்.
வரையறை 6.1
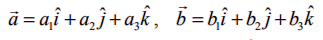 என்ற இரு வெக்டர்களின் திசையிலிப் பெருக்கல் (அல்லது புள்ளிப் பெருக்கல்)
என்ற இரு வெக்டர்களின் திசையிலிப் பெருக்கல் (அல்லது புள்ளிப் பெருக்கல்) 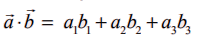 என வரையறுக்கப்படுகிறது.
என வரையறுக்கப்படுகிறது.
மேலும், 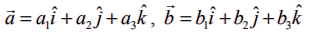 என்ற இரு வெக்டர்களின் வெக்டர் பெருக்கல் அல்லது குறுக்குப் பெருக்கல்
என்ற இரு வெக்டர்களின் வெக்டர் பெருக்கல் அல்லது குறுக்குப் பெருக்கல் 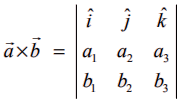 என வரையறுக்கப்படுகிறது.
என வரையறுக்கப்படுகிறது.
குறிப்பு
![]() ஒரு திசையிலியாகும், மற்றும்
ஒரு திசையிலியாகும், மற்றும் ![]() ஒரு வெக்டராகும்.
ஒரு வெக்டராகும்.
1. வடிவக்கணித விளக்கம் (Geometrical interpretation)
![]() என்பது ஏதேனுமொரு வெக்டர் மற்றும்
என்பது ஏதேனுமொரு வெக்டர் மற்றும் ![]() ஒரு அலகு வெக்டர் எனில்
ஒரு அலகு வெக்டர் எனில் ![]() −ன் மீதான
−ன் மீதான ![]() ன் வீழல்
ன் வீழல் ![]() ஆகும்.
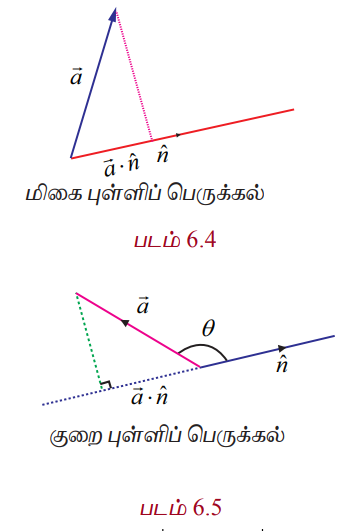
ஆகும். ![]() மற்றும்
மற்றும் ![]() ஆகியவற்றுக்கு இடைப்பட்ட கோணம் குறுங்கோணம் (படம் 6.4). எனில்,
ஆகியவற்றுக்கு இடைப்பட்ட கோணம் குறுங்கோணம் (படம் 6.4). எனில், ![]() –ன் மதிப்பு மிகை மதிப்பாகும்.
–ன் மதிப்பு மிகை மதிப்பாகும். ![]() மற்றும்
மற்றும் ![]() ஆகியவற்றுக்கு இடைப்பட்ட கோணம் விரிகோணம் எனில்,
ஆகியவற்றுக்கு இடைப்பட்ட கோணம் விரிகோணம் எனில், ![]() -ன் மதிப்பு குறை மதிப்பாகும். (படம் 6.5).
-ன் மதிப்பு குறை மதிப்பாகும். (படம் 6.5).
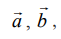 என்பன ஏதேனுமிரு பூச்சியமற்ற வெக்டர்கள் எனில்,
என்பன ஏதேனுமிரு பூச்சியமற்ற வெக்டர்கள் எனில், 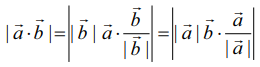 என எழுதலாம். எனவே,
என எழுதலாம். எனவே, 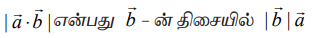 –ன் வீழலைக் காணும் போது கிடைக்கும் கோட்டுத்துண்டின் நீளம் அல்லது
–ன் வீழலைக் காணும் போது கிடைக்கும் கோட்டுத்துண்டின் நீளம் அல்லது 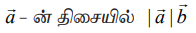 –ன் வீழலைக் காணும் போது கிடைக்கும் கோட்டுத்துண்டின் நீளம் ஆகும். மேலும்,
–ன் வீழலைக் காணும் போது கிடைக்கும் கோட்டுத்துண்டின் நீளம் ஆகும். மேலும், 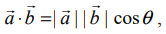 இங்கு θ என்பது
இங்கு θ என்பது 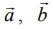 எனும் வெக்டர்களுக்கு இடைப்பட்ட கோணம் ஆகும்.
எனும் வெக்டர்களுக்கு இடைப்பட்ட கோணம் ஆகும்.
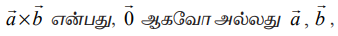 என்ற வெக்டர்களுக்கு இணையாக உள்ள தளத்திற்குச் செங்குத்தாகவும்,
என்ற வெக்டர்களுக்கு இணையாக உள்ள தளத்திற்குச் செங்குத்தாகவும், 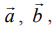 என்ற வெக்டர்களை ஒரு புள்ளியில் சந்திக்கும் அடுத்தடுத்த பக்கங்களாகக் கொண்ட இணைகரத்தின் பரப்பளவினை எண்ணளவாகவும் கொண்ட வெக்டராகும்.
என்ற வெக்டர்களை ஒரு புள்ளியில் சந்திக்கும் அடுத்தடுத்த பக்கங்களாகக் கொண்ட இணைகரத்தின் பரப்பளவினை எண்ணளவாகவும் கொண்ட வெக்டராகும். 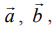 எனும் பூச்சியமற்ற வெக்டர்களுக்கு இடைப்பட்ட கோணம் θ எனில்,
எனும் பூச்சியமற்ற வெக்டர்களுக்கு இடைப்பட்ட கோணம் θ எனில், ![]() −ன் எண்ணளவினை P
−ன் எண்ணளவினை P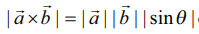 எனும் சூத்திரத்தைப் பயன்படுத்திக் காணலாம்.
எனும் சூத்திரத்தைப் பயன்படுத்திக் காணலாம்.
ஒரே தொடக்கப்புள்ளியைப் பெற்றுள்ள இரண்டு வெக்டர்கள் ஒரே தொடக்கப்புள்ளி வெக்டர்கள் அல்லது ஒரு முனையில் சந்திக்கும் வெக்டர்கள் எனப்படும்.
குறிப்புரை
(1) 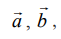 எனும் இரண்டு பூச்சியமற்ற வெக்டர்களுக்கு இடைப்பட்ட கோணம்
எனும் இரண்டு பூச்சியமற்ற வெக்டர்களுக்கு இடைப்பட்ட கோணம் 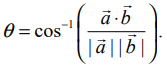
(2) 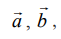 எனும் இரண்டு வெக்டர்களுக்கு இடைப்பட்ட கோணம் 0 அல்லது π எனில், அவ்வெக்டர்கள் இணையானவை.
எனும் இரண்டு வெக்டர்களுக்கு இடைப்பட்ட கோணம் 0 அல்லது π எனில், அவ்வெக்டர்கள் இணையானவை.
(3) 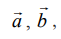 எனும் இரண்டு வெக்டர்களுக்கு இடைப்பட்ட கோணம் π/2 அல்லது 3π/2 எனில், அவ்வெக்டர்கள் செங்குத்தானவை.
எனும் இரண்டு வெக்டர்களுக்கு இடைப்பட்ட கோணம் π/2 அல்லது 3π/2 எனில், அவ்வெக்டர்கள் செங்குத்தானவை.
பண்பு
(1) 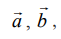 என்பன ஏதேனுமிரு வெக்டர்கள் என்க. பின்னர்,
என்பன ஏதேனுமிரு வெக்டர்கள் என்க. பின்னர்,
• 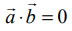 என இருந்தால், இருந்தால் மட்டுமே
என இருந்தால், இருந்தால் மட்டுமே 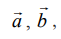 என்பவை ஒன்றுக்கொன்று செங்குத்தானவை ஆகும்.
என்பவை ஒன்றுக்கொன்று செங்குத்தானவை ஆகும்.
• 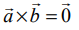 என இருந்தால், இருந்தால் மட்டுமே
என இருந்தால், இருந்தால் மட்டுமே 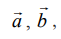 என்பவை ஒன்றுக்கொன்று இணையானவை ஆகும்.
என்பவை ஒன்றுக்கொன்று இணையானவை ஆகும்.
(2) 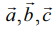 என்பன ஏதேனும் மூன்று வெக்டர்கள் மற்றும் α ஒரு திசையிலி எனில்,
என்பன ஏதேனும் மூன்று வெக்டர்கள் மற்றும் α ஒரு திசையிலி எனில்,
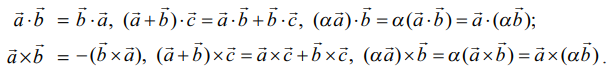
2. முக்கோணவியலில் புள்ளி மற்றும் குறுக்குப் பெருக்கல்களின் பயன்பாடு (Application of dot and cross products in plane Trigonometry)
எடுத்துக்காட்டு 6.1 (கொசைன் சூத்திரம்) (Cosine formulae)
வழக்கமான குறியீடுகளுடன், முக்கோணம் ABC−ல், வெக்டர்களைப் பயன்படுத்தி பின்வருவனவற்றை நிறுவுக.
(i) a2 = b2 + c2 − 2bc cos A
(ii) b2 = c2 + a2 − 2ca cos B
(iii) c2 = a2 + b2 − 2ab cos C
தீர்வு
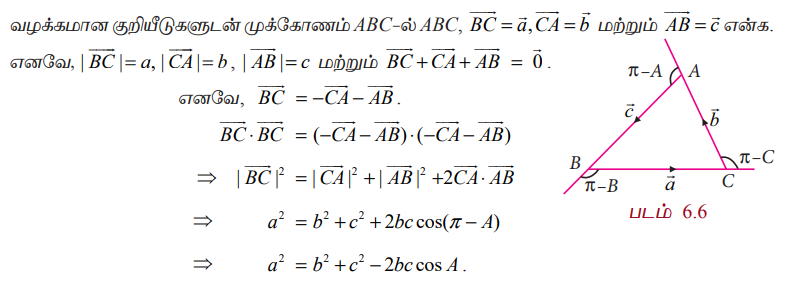
⇒ a2 = b2 + c2 + 2bc cos(π−A).
⇒ a2 = b2 + c2 − 2bc cosA.
முடிவுகள் (ii) மற்றும் (iii) ஆகியவற்றை இதே போல் நிறுவலாம்.
எடுத்துக்காட்டு 6.2
வழக்கமான குறியீடுகளுடன், முக்கோணம் ABC−ல், வெக்டர்களைப் பயன்படுத்தி பின்வருவனவற்றை நிறுவுக.
(i) a = bcosC + ccos B
(ii) b = ccos A + acosC
(iii) c = acos B + bcos A
தீர்வு

⇒ a2 = abcos C + accos B
எனவே a = bcosC + ccosB . முடிவுகள் (ii) மற்றும் (iii) ஆகியவற்றை இதேபோல் நிறுவலாம்.
எடுத்துக்காட்டு 6.3
வெக்டர் முறையில், cos(α+β) = cosα cosβ − sinα sinβ என நிறுவுக.
தீர்வு
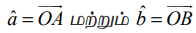 என்ற அலகு வெக்டர்கள் x−அச்சின் மிகை திசையுடன் முறையே α, β என்ற கோணங்களை ஏற்படுத்துகிறது என்க. இங்கு A, B என்பன படம் 6.8−ல் காட்டப்பட்டுள்ளன. AL மற்றும் BM என்பவற்றை x−அச்சுக்கு செங்குத்தாக வரைக.
என்ற அலகு வெக்டர்கள் x−அச்சின் மிகை திசையுடன் முறையே α, β என்ற கோணங்களை ஏற்படுத்துகிறது என்க. இங்கு A, B என்பன படம் 6.8−ல் காட்டப்பட்டுள்ளன. AL மற்றும் BM என்பவற்றை x−அச்சுக்கு செங்குத்தாக வரைக.
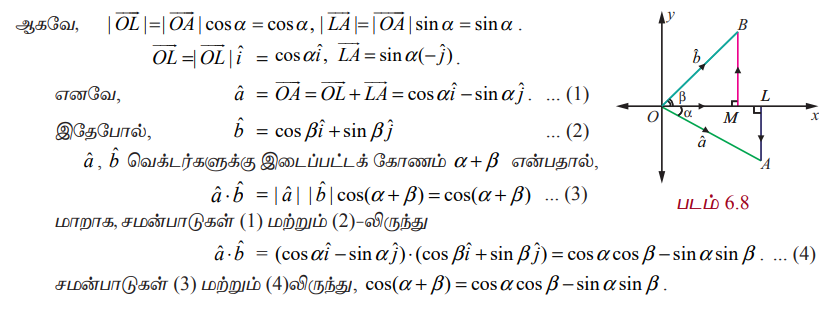
சமன்பாடுகள் (3) மற்றும் (4) லிருந்து, cos(α+β) = cos α cos β − sinα sin β.
எடுத்துக்காட்டு 6.4
வழக்கமான குறியீடுகளுடன், முக்கோணம் ABC−ல் வெக்டர்களைப் பயன்படுத்தி 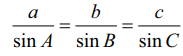 என நிறுவுக.
என நிறுவுக.
தீர்வு

எடுத்துக்காட்டு 6.5
வெக்டர்முறையில் sin(α−β) = sinα cosβ − cosα sinβ என நிறுவுக.
தீர்வு
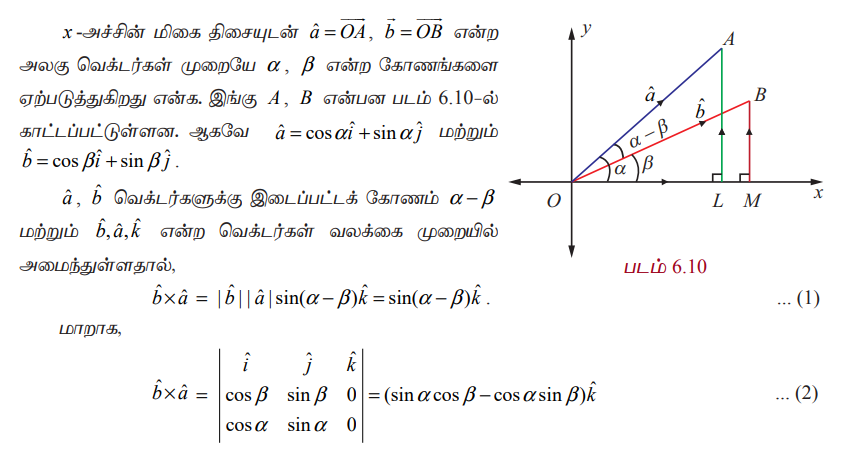
ஆகவே, சமன்பாடுகள் (1) மற்றும் (2)−லிருந்து
sin(α−β) = sinα cosβ − cosα sinβ
3. வடிவக் கணிதத்தில் புள்ளி மற்றும் குறுக்குப் பெருக்கல்களின் பயன்பாடு (Application of dot and cross products in Geometry)
எடுத்துக்காட்டு 6.6 (அபோலோனியஸ் தேற்றம்) (Apollonius's theorem)
முக்கோணம் ABC−ல், BC என்ற பக்கத்தின் நடுப்புள்ளி D எனில், 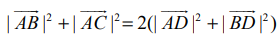 என வெக்டர் முறையில் நிரூபிக்க.
என வெக்டர் முறையில் நிரூபிக்க.
தீர்வு

எடுத்துக்காட்டு 6.7
ஒரு முக்கோணத்தின் உச்சிகளிலிருந்து அவற்றிற்கு எதிரேயுள்ள பக்கங்களுக்கு வரையப்படும் செங்குத்துக் கோடுகள் ஒரு புள்ளியில் சந்திக்கும் என நிறுவுக.
தீர்வு

எடுத்துக்காட்டு 6.8
முக்கோணம் ABC −ல், BC, CA மற்றும் AB என்ற பக்கங்களின் மையப்புள்ளிகள் முறையே D,E,F எனில், ∆DEF –ன்பரப்பு = 1/4 (∆ABC−ன் பரப்பு) என வெக்டர் முறையில் நிறுவுக.
தீர்வு
முக்கோணம் ABC−ல் ஆதிப்புள்ளி A என்க. எனவே, D, E, F என்ற புள்ளிகளின் நிலைவெக்டர்கள் முறையே 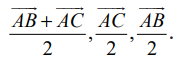 ஆகும்.
ஆகும். 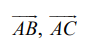 என்ற வெக்டர்களை அடுத்தடுத்த பக்கங்களாகக் கொண்ட இணைகரத்தின் பரப்பு
என்ற வெக்டர்களை அடுத்தடுத்த பக்கங்களாகக் கொண்ட இணைகரத்தின் பரப்பு 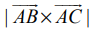 என்பதால், முக்கோணம் ∆ABC –ன் பரப்பு 1/2
என்பதால், முக்கோணம் ∆ABC –ன் பரப்பு 1/2 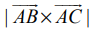 ஆகும். இதேபோன்று, ∆DEF –ஐக் கருதுக.
ஆகும். இதேபோன்று, ∆DEF –ஐக் கருதுக.
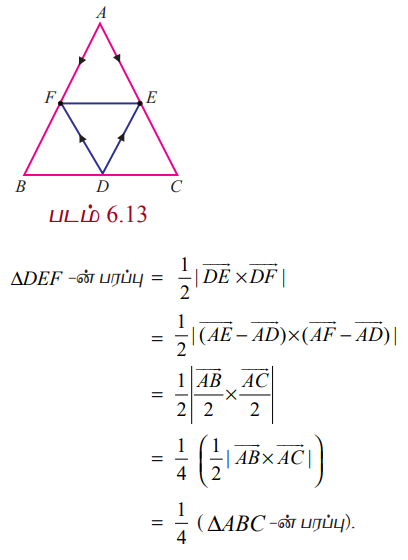
4. இயற்பியலில் புள்ளி மற்றும் குறுக்குப் பெருக்கல்களின் பயன்பாடு (Application of dot and cross product in Physics)
வரையறை 6.2
விசை ![]() −ன் செயல்பாட்டினால் ஒரு துகளானது ஒரு புள்ளியிலிருந்து மற்றொரு புள்ளிக்கு நகரும்போது அதன் இடப்பெயர்ச்சி வெக்டர்
−ன் செயல்பாட்டினால் ஒரு துகளானது ஒரு புள்ளியிலிருந்து மற்றொரு புள்ளிக்கு நகரும்போது அதன் இடப்பெயர்ச்சி வெக்டர் ![]() எனில், அவ்விசை செய்த வேலை
எனில், அவ்விசை செய்த வேலை 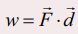 ஆகும்.
ஆகும்.
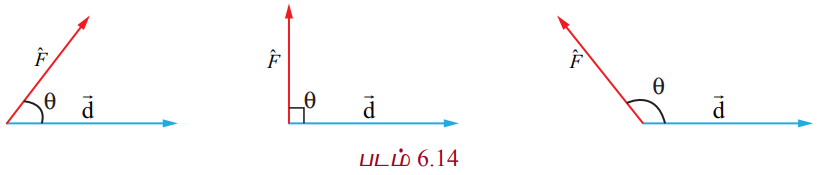
ஒரு விசை ஏற்படுத்தும் கோணம் குறுங்கோணம், செங்கோணம் மற்றும் விரிகோணம் எனில், அவ்விசை செய்யும் வேலை முறையே மிகை, பூச்சியம், மற்றும் குறை ஆகும்.
எடுத்துக்காட்டு 6.9
ஒரு துகள் (4,−3,−2) என்ற புள்ளியிலிருந்து (6,1,−3) என்ற புள்ளிக்கு 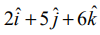 மற்றும்
மற்றும் 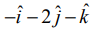 என்ற மாறாத விசைகளின் செயல்பாட்டினால் நகர்த்தப்பட்டால், அவ்விசைகள் செய்த மொத்த வேலையைக் காண்க.
என்ற மாறாத விசைகளின் செயல்பாட்டினால் நகர்த்தப்பட்டால், அவ்விசைகள் செய்த மொத்த வேலையைக் காண்க.
தீர்வு
கொடுக்கப்பட்ட விசைகளின் விளைவு விசை 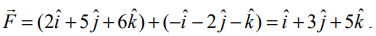 A, B என்பவை குறிக்கும் புள்ளிகள் முறையே (4,−3,−2), (6,1,−3) என்க. துகளின் இடப்பெயர்ச்சி வெக்டர்
A, B என்பவை குறிக்கும் புள்ளிகள் முறையே (4,−3,−2), (6,1,−3) என்க. துகளின் இடப்பெயர்ச்சி வெக்டர் 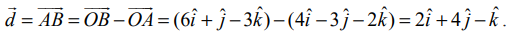 , எனவே, விசைகள் செய்த மொத்த வேலை
, எனவே, விசைகள் செய்த மொத்த வேலை 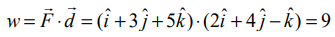 அலகுகள்.
அலகுகள்.
எடுத்துக்காட்டு 6.10
ஒரு துகள் (1,3,−1) என்ற புள்ளியிலிருந்து (4,−1,λ) என்ற புள்ளிக்கு 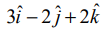 மற்றும்
மற்றும் 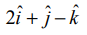 என்ற விசைகளின் செயல்பாட்டினால் நகர்த்தப்படுகிறது. அவ்விசைகள் செய்த வேலை 16 அலகுகள் எனில், λ−ன் மதிப்பைக் காண்க.
என்ற விசைகளின் செயல்பாட்டினால் நகர்த்தப்படுகிறது. அவ்விசைகள் செய்த வேலை 16 அலகுகள் எனில், λ−ன் மதிப்பைக் காண்க.
தீர்வு
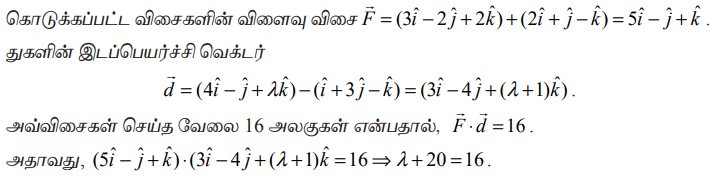
எனவே, λ = −4 எனப் பெறுகிறோம்
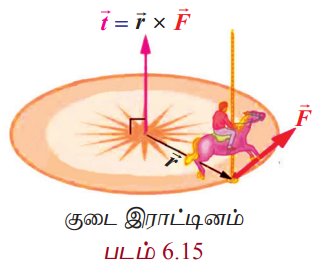
வரையறை 6.3
![]() என்ற விசையை,
என்ற விசையை, ![]() –ஐ நிலைவெக்டராகக் கொண்ட புள்ளியில் உள்ள துகளின் மீது செயல்படுத்துவதால், அத்துகளின் மீதான முறுக்குத்திறன் அல்லது திருப்புத்திறன்
–ஐ நிலைவெக்டராகக் கொண்ட புள்ளியில் உள்ள துகளின் மீது செயல்படுத்துவதால், அத்துகளின் மீதான முறுக்குத்திறன் அல்லது திருப்புத்திறன் 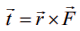 ஆகும். திருப்புவிசை என்பது சுழல் விசை எனவும் அழைக்கப்படும்.
ஆகும். திருப்புவிசை என்பது சுழல் விசை எனவும் அழைக்கப்படும்.
எடுத்துக்காட்டு 6.11
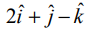 என்னும் விசை ஆதிப்புள்ளி வழியாகச் செயல்படுகிறது எனில், (2,0,−1) என்ற புள்ளியைப் பொறுத்து அவ்விசையின் திருப்புவிசையின் எண்ணளவு மற்றும் திசைக்கொசைன்களைக் காண்க.
என்னும் விசை ஆதிப்புள்ளி வழியாகச் செயல்படுகிறது எனில், (2,0,−1) என்ற புள்ளியைப் பொறுத்து அவ்விசையின் திருப்புவிசையின் எண்ணளவு மற்றும் திசைக்கொசைன்களைக் காண்க.
தீர்வு
