கொடுக்கப்பட்ட ஒரே கோட்டிலமையாத மூன்று புள்ளிகள் வழியாகச் செல்லும் தளத்தின் சமன்பாடு (Equation of a plane passing through three given non−collinear points)

4. கொடுக்கப்பட்ட ஒரே கோட்டிலமையாத மூன்று புள்ளிகள் வழியாகச் செல்லும் தளத்தின் சமன்பாடு (Equation of a plane passing through three given non−collinear points)

(a) துணையலகு வெக்டர் சமன்பாடு (Parametric form of vector equation)

தேற்றம் 6.17

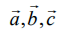என்பன ஒரே கோட்டிலமையாத மூன்று புள்ளிகளின் நிலை வெக்டர்கள் எனில், கொடுக்கப்பட்ட இம்மூன்று புள்ளிகள் வழியாகச் செல்லும் தளத்தின் துணையலகு வெக்டர் சமன்பாடு

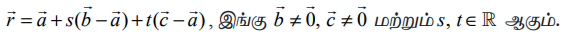
நிரூபணம்

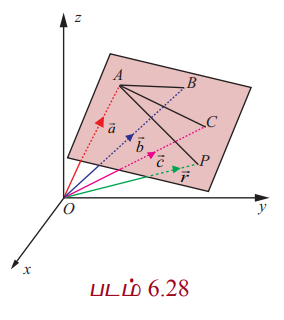
ஒரே கோட்டிலமையாத முறையே 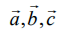என்ற வெக்டர்களை நிலை வெக்டர்களாகக் கொண்ட A,B,C என்ற புள்ளிகள் வழியாக தேவையான தளம் செல்கிறது என்க. ஆகவே, இவற்றில் குறைந்தது இரு வெக்டர்கள் பூச்சியமற்ற வெக்டர்களாக இருக்கும். நாம் 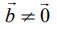மற்றும் 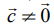எனக் கொள்வோம். தளத்தின் மீதுள்ள ஏதேனும் ஒரு புள்ளி P –ன் நிலைவெக்டர் என்க. 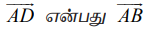−க்கு இணையாக இருக்குமாறும் மற்றும்  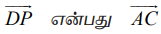−க்கு இணையாக இருக்குமாறும் AB −ஐ நீட்டித்து அதன் மேல் D என்ற புள்ளியை எடுத்துக் கொள்க. எனவே,

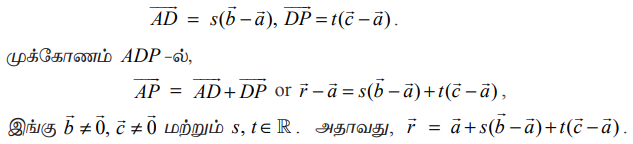
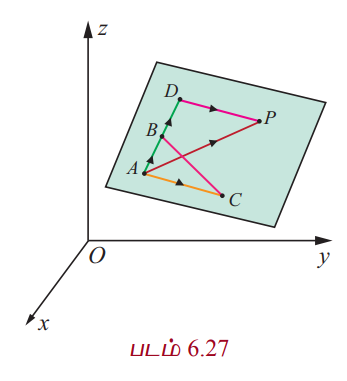
இது கொடுக்கப்பட்ட ஒரே கோட்டிலமையாத மூன்று புள்ளிகள் வழியாகச் செல்லும் தளத்தின் துணையலகு வெக்டர் சமன்பாடாகும்.

(b) துணையலகு அல்லாத வெக்டர் சமன்பாடு (Non−parametric form of vector equation) 

ஒரே கோட்டிலமையாத முறையே 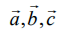என்ற வெக்டர்களை நிலைவெக்டர்களாகக் கொண்ட A, B, C என்ற புள்ளிகள் வழியாகத் தேவையான தளம் செல்கிறது என்க. ஆகவே இவற்றில் குறைந்தது இரு வெக்டர்களாவது பூச்சியமற்றதாக இருக்கும். நாம்  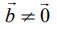மற்றும் 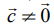எனக் கொள்வோம்.

இது ஒரே கோட்டிலமையாத மூன்று புள்ளிகள் வழிச் செல்லும் தளத்தின் துணையலகு அல்லாத வெக்டர்ச மன்பாடாகும்.

(c) கார்டீசியன் சமன்பாடு (Cartesian form of equation)

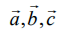என்ற நிலைவெக்டர்களைக் கொண்ட ஒரே கோட்டிலமையாத மூன்று புள்ளிகள் A,B,C என்பவற்றின் அச்சுத்தூரங்கள் முறையே (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) மற்றும் என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட P என்ற புள்ளியின் அச்சுத்தூரங்கள் (x,y,z) எனில்,

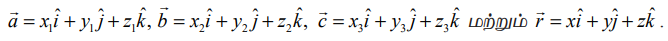
இவ்வெக்டர்களைப் பயன்படுத்தி, ஒரே கோட்டிலமையாத கொடுக்கப்பட்ட மூன்று புள்ளிகள் வழிச் செல்லும் தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாட்டினை பின்வருமாறு எழுதலாம்.

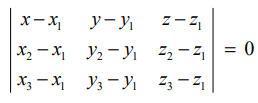
இதுவே ஒரே கோட்டிலமையாத மூன்று புள்ளிகள் வழிச் செல்லும் தளத்தின் கார்டீசியன் சமன்பாடாகும்.