ஒரு தளத்தின் பல்வேறு வகைச் சமன்பாடுகள் (Different forms of Equation of a plane)

ஒரு தளத்தின் பல்வேறு வகைச் சமன்பாடுகள் (Different forms of Equation of a plane)

தளம் என்பதன் கருத்தாக்கத்தை நாம் ஏற்கனவே கற்றறிந்துள்ளோம்.

வரையறை 6.8

ஒரு தளத்திற்குச் செங்குத்தாக உள்ள வெக்டர் அத்தளத்தின் செங்குத்து அல்லது செங்கோடு என்கிறோம்.

குறிப்பு

ஒரு தளத்தின் செங்கோடானது, அத்தளத்தில் உள்ள ஒவ்வொரு நேர்க்கோட்டிற்கும் செங்குத்தாகும்.

பின்வருவனவற்றில் ஏதேனும் ஒன்று கொடுக்கப்பட்டால், ஒரு தளத்தை தனித்ததாக தீர்மானிக்கலாம் :

• தளத்திற்குச் செங்குத்தான ஓரலகு வெக்டர் மற்றும் ஆதிப்புள்ளியில் இருந்து அத்தளத்திற்கு உள்ள தூரம்.

• தளத்தின் மீதான ஒரு புள்ளி மற்றும் தளத்தின் ஒரு செங்கோடு.

• ஒரே கோட்டிலமையாத மூன்று புள்ளிகள்.

• தளத்தின் மீதுள்ள ஒரு புள்ளி மற்றும் தளத்திற்கு இணையாக உள்ள இரண்டு இணை அல்லாத கோடுகள் அல்லது வெக்டர்கள்.

• தளத்தின் மீதுள்ள இரு தனித்த புள்ளிகள் மற்றும் தளத்திற்கு இணையாக உள்ள ஆனால் இவ்விரு புள்ளிகளைச் சேர்க்கும் கோட்டிற்கு இணையாக இல்லாத ஒரு நேர்க்கோடு அல்லது ஒரு பூச்சியமற்ற வெக்டர்.

தளங்களின் வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளை மேற்கண்ட நிலைகளைப் பயன்படுத்திக் காண்போம்.

1. தளத்தின் ஒரு செங்கோடு மற்றும் ஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் கொடுக்கப்பட்டால் தளத்தின் சமன்பாடு (Equation of a plane when a normal to the plane and the distance of the plane from the origin are given)

(a) செங்கோட்டு வடிவ வெக்டர் சமன்பாடு (Vector equation of a plane in normal form)

தேற்றம் 6.15

ஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் p மற்றும் தளத்திற்குச் செங்குத்தான ஓரலகு வெக்டர் எனில், தளத்தின் சமன்பாடு 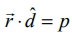ஆகும். 

நிரூபணம்

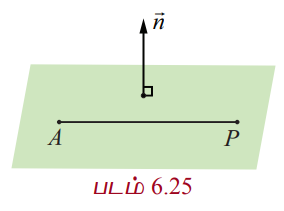
ஆதிப்புள்ளியிலிருந்து p தொலைவில் உள்ள தளத்தினை கருதுக. ஆதிப்புள்ளி  O−விலிருந்து தளத்திற்கு வரையப்படும் செங்கோட்டின் அடி A என்க.

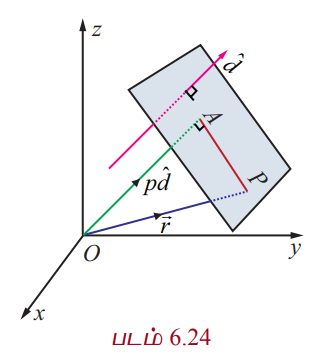
−ன் திசையில் உள்ள ஓரலகு செங்குத்து வெக்டர் என்க. பின்னர், 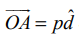ஆகும்.

என்பது தளத்தில் உள்ள ஏதேனும் ஒரு புள்ளி P−ன் நிலைவெக்டர் எனில், 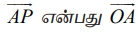வுக்குச் செங்குத்தாகும். 

எனவே,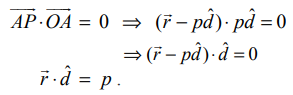

இச்சமன்பாடு, தளத்தின் செங்கோட்டு வடிவ வெக்டர் சமன்பாடு எனப்படும்.

(b) செங்கோட்டு வடிவ கார்டீசியன் சமன்பாடு (Cartesian equation of a plane in normal form) 

–ன் திசைக்கொசைன்கள் 1,m,n என்க. எனவே, 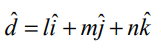ஆகும்.

இதனைச் சமன்பாடு (1)−ல் பிரதியிட,

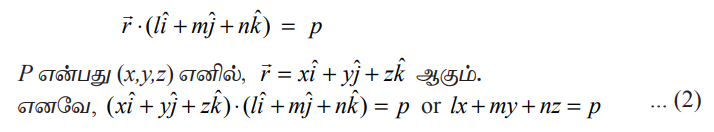
சமன்பாடு (2) ஆனது தளத்தின் செங்கோட்டு வடிவ கார்டீசியன் சமன்பாடு எனப்படும்.

குறிப்புரை

(i) ஆதிப் புள்ளி வழியாக தளம் செல்லுமெனில், p = 0 ஆகும். எனவே, தளத்தின் சமன்பாடு lx + my + nz = 0.

(ii)  என்பது தளத்திற்கு செங்குத்தான வெக்டர் எனில், 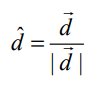என்பது தளத்திற்குச் செங்குத்தான ஓரலகு வெக்டராகும். எனவே, தளத்தின் சமன்பாடு 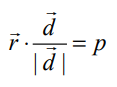அல்லது 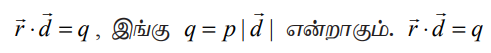என்ற சமன்பாடு தளத்தின் திட்ட வடிவ வெக்டர் சமன்பாடு எனப்படும்.

குறிப்பு

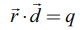என்ற திட்ட வடிவச் சமன்பாட்டில், என்பது ஓரலகு செங்குத்து வெக்டராகவோ, q என்பது செங்குத்துத் தொலைவாகவோ இருக்கத் தேவையில்லை.

2. ஒரு வெக்டருக்கு செங்குத்தாக கொடுக்கப்பட்ட ஒரு புள்ளி வழியாகச் செல்லும் தளத்தின் சமன்பாடு (Equation of a plane perpendicular to a vector and passing through a given point)

(a) வெக்டர் சமன்பாடு (Vector form of equation)

என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளி A வழியாகச் செல்வதும் க்கு செங்குத்தானதுமான தளத்தைக் கருதுக.

தளத்தின் மீதுள்ள ஏதேனும் ஒரு புள்ளி P−ன் நிலை வெக்டர் என்க.

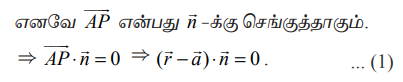
இச்சமன்பாடு என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளி வழியாகச் செல்வதும் −க்கு செங்குத்தானதுமான தளத்தின் வெக்டர் சமன்பாடாகும்.

குறிப்பு

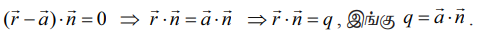
(b) கார்டீசியன் சமன்பாடு (Cartesian form of equation)

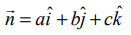a,b,c என்பன -ன் திசை விகிதங்கள் எனில், ஆகும். A−ன் அச்சுத்தூரங்கள் (x1 ,y1, z1) என்க. எனவே, சமன்பாடு (1)லிருந்து,

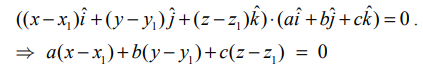
இது (x1 ,y1, z1) என்ற புள்ளி வழியாகச் செல்வதும் a,b,c என்பவற்றை திசை விகிதங்களாகக் கொண்ட வெக்டருக்கு செங்குத்தானதுமான தளத்தின் கார்டீசியன் சமன்பாடாகும். 

3. தளத்தின் வெட்டுத்துண்டு வடிவச் சமன்பாடு (Intercept form of the equation of a plane)

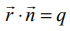என்ற தளம் OA = a, OB = b, OC = c என்ற வெட்டுத் துண்டுகளை ஏற்படுத்துமாறு ஆய அச்சுக்களை A, B, C என்ற புள்ளிகளில் சந்திக்கிறது என்க. எனவே, A−ன் நிலை வெக்டர் ஆகும்.

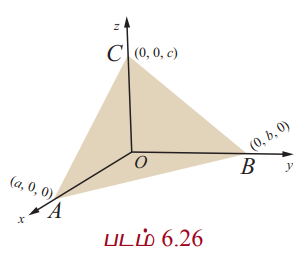
A என்ற இப்புள்ளி கொடுக்கப்பட்ட தளத்தின் மீது உள்ளதால், 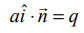ஆகும். இதிலிருந்து 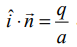ஆகும்.

இது a,b,c என்ற வெட்டுத் துண்டுகளை முறையே x,y,z அச்சுக்களில் ஏற்படுத்தும் தளத்தின் வெட்டுத் துண்டு வடிவச்ச மன்பாடாகும்.

தேற்றம் 6.16

x, y, z−ல் உள்ள ax + by+ cz + d = 0 என்ற நேரியச் சமன்பாடு ஒரு தளத்தைக் குறிக்கும்.

நிரூபணம்

 ax + by + cz + d = 0 என்ற சமன்பாட்டை வெக்டர் சமன்பாடாக 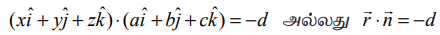  என எழுதலாம்.

இச்சமன்பாடு ஒரு தளத்தின் திட்ட வடிவ வெக்டர் சமன்பாடாகும். எனவே, கொடுக்கப்பட்ட சமன்பாடு ax+by+cz+d=0 என்பது ஒரு தளத்தைக் குறிக்கிறது. இங்கு 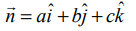என்ற வெக்டர் தளத்திற்குச் செங்குத்தான வெக்டராகும்.

குறிப்பு

ஒரு தளத்தின் பொது வடிவச் சமன்பாடு ax + by + cz + d = 0 –ல் உள்ள a,b,c என்பன தளத்தின் செங்குத்தின் அல்லது செங்கோட்டின் திசை விகிதங்கள் ஆகும்.

எடுத்துக்காட்டு 6.38

ஆதியில் இருந்து 12 அலகுகள் தூரத்தில் இருப்பதும் 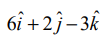என்ற வெக்டருக்குச் செங்குத்தானதாகவும் உள்ள தளத்தின் வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.

தீர்வு

என்பது தளத்தில் உள்ள ஏதேனுமொரு புள்ளி (x,y,z) –ன் நிலைவெக்டர் எனில், தளத்தின் செங்கோட்டு வடிவ வெக்டர் சமன்பாடு 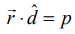-ஐப் பயன்படுத்தி நாம் பெறுவது,

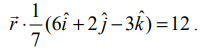
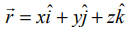என இச்சமன்பாட்டில் பிரதியிடக் கிடைப்பது  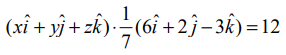 புள்ளிப் பெருக்கலைப் பயன்படுத்திச் சுருக்கினால் கிடைக்கும் 6x+2y−3z=84 என்ற சமன்பாடு தேவையான தளத்தின் கார்டீசியன் சமன்பாடாகும்.

எடுத்துக்காட்டு 6.39

ஒரு தளத்தின் கார்டீசியன் சமன்பாடு 3x−4y+3z=−8 எனில், தளத்தின் வெக்டர் சமன்பாட்டை திட்ட வடிவில் காண்க.

தீர்வு

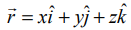என்பது தளத்தில் உள்ள ஏதேனுமொரு புள்ளி (x,y,z)  நிலை வெக்டர் என்க. கொடுக்கப்பட்ட சமன்பாட்டை 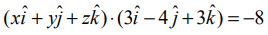அல்லது 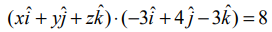என எழுதலாம். அதாவது, 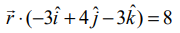இது கொடுக்கப்பட்ட தளத்தின் திட்ட வடிவ வெக்டர் சமன்பாடாகும்.

எடுத்துக்காட்டு 6.40

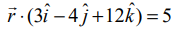என்ற தளத்தின் செங்குத்தின் திசைக்கொசைன்கள் மற்றும் ஆதியிலிருந்து தளத்திற்கு வரையப்படும் செங்குத்தின் நீளம் ஆகியவற்றைக் காண்க.

தீர்வு

எடுத்துக்காட்டு 6.41

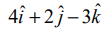என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளி வழிச் செல்வதும் 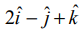என்ற வெக்டருக்குச் செங்குத்தானதுமான தளத்தின் வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.

தீர்வு

கொடுக்கப்பட்ட புள்ளியின் நிலை வெக்டர் 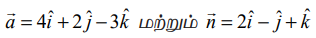என்க. கொடுக்கப்பட்ட புள்ளி வழியாகச் செல்வதும், தளத்திற்குச் செங்குத்தான வெக்டரைக் கொண்டதுமான தளத்தின் வெக்டர் சமன்பாடு

எனவே, தேவையான தளத்தின் வெக்டர் சமன்பாடு காண இச்சமன்பாட்டில் 

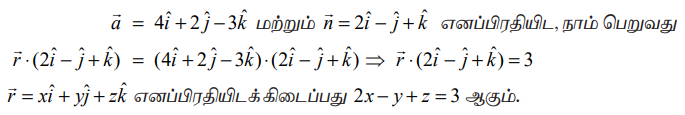
இதுவே தேவையான தளத்தின் கார்டீசியன் சமன்பாடாகும்.

எடுத்துக்காட்டு 6.42

ஒரு நகரும் தளம் ஆய அச்சுக்களில் ஏற்படுத்தும் வெட்டுத்துண்டுகளின் தலை கீழிகளின் கூடுதல் ஒரு மாறிலியாக இருக்குமாறு நகர்கிறது எனில், அத்தளமானது ஒரு நிலைத்த புள்ளி வழியாகச் செல்கிறது எனக் காட்டுக.

தீர்வு

x,y,z அச்சுக்களில் முறையே a,b,c என்ற வெட்டுத் துண்டுகளை ஏற்படுத்தும் தளத்தின் சமன்பாடு 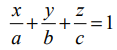ஆகும். ஆய அச்சுக்களில் ஏற்படுத்தும் வெட்டுத்துண்டுகளின் தலை கீழிகளின் கூடுதல் ஒருமாறிலி என்பதால் 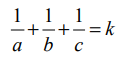ஆகும். இங்கு, k ஒரு மாறிலி. இதனை 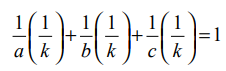என எழுதலாம்.

இச்சமன்பாடு, என்ற நிலைத்தப் புள்ளி வழியாகச் செல்கிறது எனக்காட்டுகிறது.