12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்

தளத்தின் வெட்டுத்துண்டு வடிவச் சமன்பாடு (Intercept form of the equation of a plane)

இது a,b,c என்ற வெட்டுத் துண்டுகளை முறையே x,y,z அச்சுக்களில் ஏற்படுத்தும் தளத்தின் வெட்டுத் துண்டு வடிவச்ச மன்பாடாகும்.

3. தளத்தின் வெட்டுத்துண்டு வடிவச் சமன்பாடு (Intercept form of the equation of a plane)

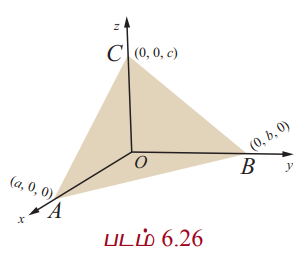
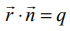என்ற தளம் OA = a, OB = b, OC = c என்ற வெட்டுத் துண்டுகளை ஏற்படுத்துமாறு ஆய அச்சுக்களை A, B, C என்ற புள்ளிகளில் சந்திக்கிறது என்க. எனவே, A−ன் நிலை வெக்டர் ஆகும்.

A என்ற இப்புள்ளி கொடுக்கப்பட்ட தளத்தின் மீது உள்ளதால், 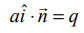ஆகும். இதிலிருந்து 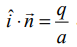ஆகும்.

தேற்றம் 6.16

x, y, z−ல் உள்ள ax + by+ cz + d = 0 என்ற நேரியச் சமன்பாடு ஒரு தளத்தைக் குறிக்கும்.

நிரூபணம்

ax + by + cz + d = 0 என்ற சமன்பாட்டை வெக்டர் சமன்பாடாக 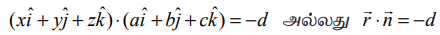என எழுதலாம்.

இச்சமன்பாடு ஒரு தளத்தின் திட்ட வடிவ வெக்டர் சமன்பாடாகும். எனவே, கொடுக்கப்பட்ட சமன்பாடு ax+by+cz+d=0 என்பது ஒரு தளத்தைக் குறிக்கிறது. இங்கு 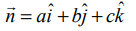என்ற வெக்டர் தளத்திற்குச் செங்குத்தான வெக்டராகும்.

குறிப்பு

ஒரு தளத்தின் பொது வடிவச் சமன்பாடு ax + by + cz + d = 0 –ல் உள்ள a,b,c என்பன தளத்தின் செங்குத்தின் அல்லது செங்கோட்டின் திசை விகிதங்கள் ஆகும்.

எடுத்துக்காட்டு 6.38

ஆதியில் இருந்து 12 அலகுகள் தூரத்தில் இருப்பதும் 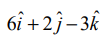என்ற வெக்டருக்குச் செங்குத்தானதாகவும் உள்ள தளத்தின் வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.

தீர்வு

என்பது தளத்தில் உள்ள ஏதேனுமொரு புள்ளி (x,y,z) –ன் நிலைவெக்டர் எனில், தளத்தின் செங்கோட்டு வடிவ வெக்டர் சமன்பாடு 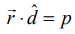-ஐப் பயன்படுத்தி நாம் பெறுவது,

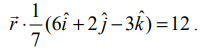
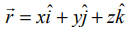என இச்சமன்பாட்டில் பிரதியிடக் கிடைப்பது 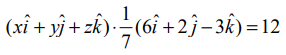புள்ளிப் பெருக்கலைப் பயன்படுத்திச் சுருக்கினால் கிடைக்கும் 6x+2y−3z=84 என்ற சமன்பாடு தேவையான தளத்தின் கார்டீசியன் சமன்பாடாகும்.

எடுத்துக்காட்டு 6.39

ஒரு தளத்தின் கார்டீசியன் சமன்பாடு 3x−4y+3z=−8 எனில், தளத்தின் வெக்டர் சமன்பாட்டை திட்ட வடிவில் காண்க.

தீர்வு

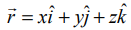என்பது தளத்தில் உள்ள ஏதேனுமொரு புள்ளி (x,y,z) நிலை வெக்டர் என்க. கொடுக்கப்பட்ட சமன்பாட்டை 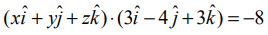அல்லது 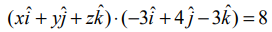என எழுதலாம். அதாவது, 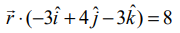இது கொடுக்கப்பட்ட தளத்தின் திட்ட வடிவ வெக்டர் சமன்பாடாகும்.

எடுத்துக்காட்டு 6.40

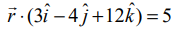என்ற தளத்தின் செங்குத்தின் திசைக்கொசைன்கள் மற்றும் ஆதியிலிருந்து தளத்திற்கு வரையப்படும் செங்குத்தின் நீளம் ஆகியவற்றைக் காண்க.

தீர்வு

எடுத்துக்காட்டு 6.41

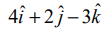என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளி வழிச் செல்வதும் 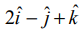என்ற வெக்டருக்குச் செங்குத்தானதுமான தளத்தின் வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.

தீர்வு

கொடுக்கப்பட்ட புள்ளியின் நிலை வெக்டர் 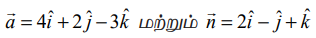என்க. கொடுக்கப்பட்ட புள்ளி வழியாகச் செல்வதும், தளத்திற்குச் செங்குத்தான வெக்டரைக் கொண்டதுமான தளத்தின் வெக்டர் சமன்பாடு

எனவே, தேவையான தளத்தின் வெக்டர் சமன்பாடு காண இச்சமன்பாட்டில்

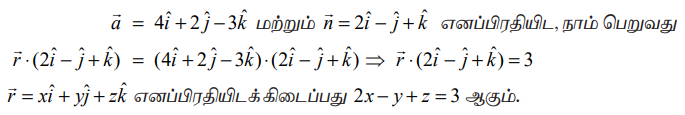
இதுவே தேவையான தளத்தின் கார்டீசியன் சமன்பாடாகும்.

எடுத்துக்காட்டு 6.42

ஒரு நகரும் தளம் ஆய அச்சுக்களில் ஏற்படுத்தும் வெட்டுத்துண்டுகளின் தலை கீழிகளின் கூடுதல் ஒரு மாறிலியாக இருக்குமாறு நகர்கிறது எனில், அத்தளமானது ஒரு நிலைத்த புள்ளி வழியாகச் செல்கிறது எனக் காட்டுக.

தீர்வு

x,y,z அச்சுக்களில் முறையே a,b,c என்ற வெட்டுத் துண்டுகளை ஏற்படுத்தும் தளத்தின் சமன்பாடு 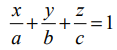ஆகும். ஆய அச்சுக்களில் ஏற்படுத்தும் வெட்டுத்துண்டுகளின் தலை கீழிகளின் கூடுதல் ஒருமாறிலி என்பதால் 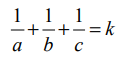ஆகும். இங்கு, k ஒரு மாறிலி. இதனை 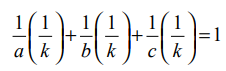என எழுதலாம்.

இச்சமன்பாடு, என்ற நிலைத்தப் புள்ளி வழியாகச் செல்கிறது எனக்காட்டுகிறது.

12th Maths : UNIT 6 : Applications of Vector Algebra : Intercept form of the equation of a plane in Tamil : 12th Standard TN Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் : தளத்தின் வெட்டுத்துண்டு வடிவச் சமன்பாடு (Intercept form of the equation of a plane) - : 12 ஆம் வகுப்பு தமிழ்நாடு பள்ளி சமசீர் புத்தகம் கேள்விகள் மற்றும் பதில்கள்.