12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்
கொடுக்கப்பட்ட இரண்டு தனித்த புள்ளிகள் வழியாகச் செல்வதும் ஒரு பூச்சியமற்ற வெக்டருக்கு இணையாகவும் உள்ள தளத்தின் சமன்பாடு (Equation of a plane passing through two given distinct points and is parallel to a non−zero vector)
6. கொடுக்கப்பட்ட இரண்டு தனித்த புள்ளிகள் வழியாகச் செல்வதும் ஒரு பூச்சியமற்ற வெக்டருக்கு இணையாகவும் உள்ள தளத்தின் சமன்பாடு (Equation of a plane passing through two given distinct points and is parallel to a non−zero vector)
(a) துணையலகு வெக்டர் சமன்பாடு (Parametric form of vector equation)
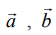 என்ற நிலை வெக்டர்களைக் கொண்ட இரு தனித்த புள்ளிகள் A மற்றும் B வழியாகச் செல்வதும்
என்ற நிலை வெக்டர்களைக் கொண்ட இரு தனித்த புள்ளிகள் A மற்றும் B வழியாகச் செல்வதும் ![]() என்ற பூச்சியமற்ற வெக்டருக்கு இணையானதுமான தளத்தின் துணையலகு வடிவ
என்ற பூச்சியமற்ற வெக்டருக்கு இணையானதுமான தளத்தின் துணையலகு வடிவ ![]() வெக்டர் சமன்பாடு
வெக்டர் சமன்பாடு

(b) துணையலகு அல்லாத வெக்டர் சமன்பாடு (Non−parametric form of vector equation)
சமன்பாடு (1)−ஐ துணையலகு அல்லாத வெக்டர் சமன்பாடாக பின்வருமாறு எழுதலாம்
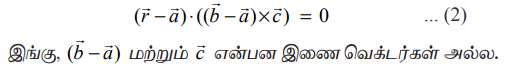
(c) கார்டீசியன் சமன்பாடு (Cartesian form of equation)
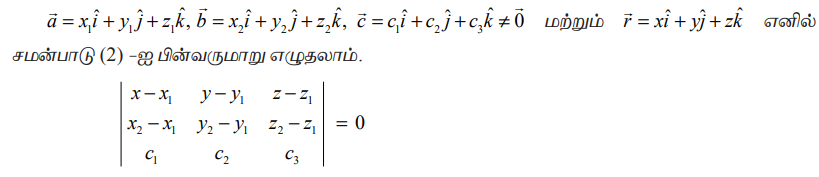
இதுவே, தேவையான தளத்தின் கார்டீசியன் சமன்பாடாகும்.
எடுத்துக்காட்டு 6.43
(0,1,−5) என்ற புள்ளி வழிச் செல்லும் 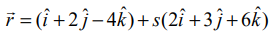 மற்றும்
மற்றும் 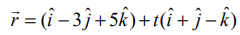 என்ற கோடுகளுக்கு இணையாக உள்ளதுமான தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
என்ற கோடுகளுக்கு இணையாக உள்ளதுமான தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு
தேவையான தளம் 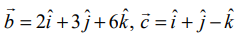 என்ற வெக்டர்களுக்கு இணையாகவும்,
என்ற வெக்டர்களுக்கு இணையாகவும், ![]() –ஐ நிலை வெக்டராகக் கொண்ட (0,1,−5) என்ற புள்ளி வழியாகவும் செல்வதைக் காண்கிறோம். மேலும்,
–ஐ நிலை வெக்டராகக் கொண்ட (0,1,−5) என்ற புள்ளி வழியாகவும் செல்வதைக் காண்கிறோம். மேலும், 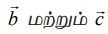 என்பன இணை வெக்டர்கள் அல்ல எனவும் காண்கிறோம்.
என்பன இணை வெக்டர்கள் அல்ல எனவும் காண்கிறோம்.
தேவையான தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாடு 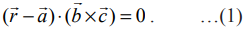
இப்பொழுது 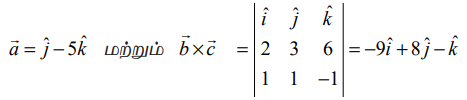 என சமன்பாடு (1)−ல் பிரதியிட, நாம்பெறுவது
என சமன்பாடு (1)−ல் பிரதியிட, நாம்பெறுவது
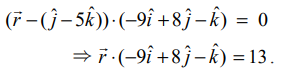
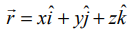 என்பது தளத்தின் மீதுள்ள ஏதேனும் ஒரு புள்ளியின் நிலைவெக்டர் எனில், மேற்கண்ட சமன்பாட்டிலிருந்து தளத்தின் கார்டீசியன் சமன்பாட்டை −9x+8y−z=13 அல்லது 9x−8y+z+13=0 எனப்பெறுகிறோம்.
என்பது தளத்தின் மீதுள்ள ஏதேனும் ஒரு புள்ளியின் நிலைவெக்டர் எனில், மேற்கண்ட சமன்பாட்டிலிருந்து தளத்தின் கார்டீசியன் சமன்பாட்டை −9x+8y−z=13 அல்லது 9x−8y+z+13=0 எனப்பெறுகிறோம்.
எடுத்துக்காட்டு 6.44
(−1,2,0), (2,2−1) என்ற புள்ளிகள் வழியாகச் செல்வதும் 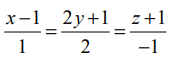 என்ற கோட்டிற்கு இணையாகவும் உள்ள தளத்தின் துணையலகு வெக்டர் சமன்பாடு, துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
என்ற கோட்டிற்கு இணையாகவும் உள்ள தளத்தின் துணையலகு வெக்டர் சமன்பாடு, துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு
தேவையான தளம் கொடுக்கப்பட்ட கோட்டிற்கு இணை என்பதால், அத்தளம் 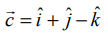 என்ற வெக்டருக்கு இணையாகும் மற்றும்
என்ற வெக்டருக்கு இணையாகும் மற்றும் 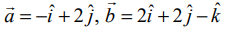 என்ற புள்ளிகள் வழியாகச் செல்லும்.
என்ற புள்ளிகள் வழியாகச் செல்லும்.
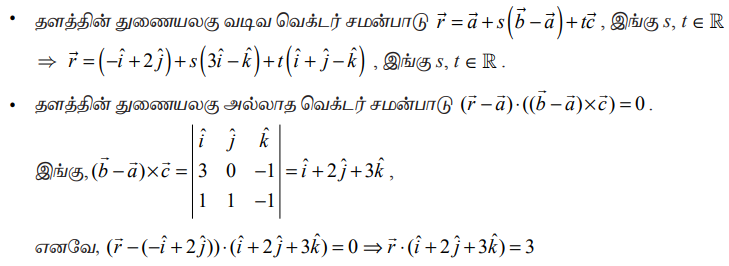
• 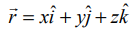 என்பது தளத்தில் உள்ள ஏதேனுமொரு புள்ளியின் நிலைவெக்டர் எனில், மேற்கண்ட சமன்பாட்டிலிருந்து தளத்தின் கார்டீசியன் சமன்பாட்டை x+2y+3z=3 எனப்பெறுகிறோம்.
என்பது தளத்தில் உள்ள ஏதேனுமொரு புள்ளியின் நிலைவெக்டர் எனில், மேற்கண்ட சமன்பாட்டிலிருந்து தளத்தின் கார்டீசியன் சமன்பாட்டை x+2y+3z=3 எனப்பெறுகிறோம்.