வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் - இரு நேர்க்கோடுகள் வெட்டும் புள்ளி (Point of intersection of two straight lines) | 12th Maths : UNIT 6 : Applications of Vector Algebra

12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்

இரு நேர்க்கோடுகள் வெட்டும் புள்ளி (Point of intersection of two straight lines)

நேர்க்கோடுகளின் சமன்பாடுகள் வெக்டர் சமன்பாடுகளாக கொடுக்கப்பட்டால், அச்சமன்பாடுகளை கார்டீசியன் சமன்பாடுகளாக மாற்றி எழுதி மேற்கண்ட முறையில் வெட்டும் புள்ளியைக் காணலாம்.

5. இரு நேர்க்கோடுகள் வெட்டும் புள்ளி (Point of intersection of two straight lines)

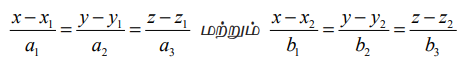என்பன இரு நேர்க்கோடுகள் எனில், இக்கோடுகளின் மீது உள்ள புள்ளிகளின் அமைப்பு முறையே (x1 + sa1, y1 + sa2, z1 +sa3) மற்றும் (x2 + tb1, y2 + tb2, z2 +tb3) ஆகும். கொடுக்கப்பட்ட கோடுகள் வெட்டிக் கொள்ளுமானால், ஒரு பொதுவான புள்ளி இருக்க வேண்டும். ஆகையால், கோடுகள் வெட்டிக்கொள்ளும் புள்ளியில், ஒரு சில s, t மதிப்புகளுக்கு,

(x1 + sa1, y1 + sa2, z1 + sa3) = (x2 +tb1, y2 +tb2, z2 +tb3)

எனவே, x1 + sa1 = x2 +tb1, y1 + sa2 = y2 +tb2, z1 + sa3 = z2 +tb3

இம்மூன்று சமன்பாடுகளில் ஏதேனும் இரு சமன்பாடுகளின் தீர்வு காண்பதால் பெறப்படும் s மற்றும் t –ன் மதிப்புகள் மீதமுள்ள சமன்பாட்டை நிறைவு செய்யுமானால், கொடுக்கப்பட்ட கோடுகள் வெட்டும் கோடுகளாகும். அவ்வாறு இல்லையெனில், அவை வெட்டாக் கோடுகளாகும். s−ன் மதிப்பை, (அல்லது t –ன் மதிப்பை) பிரதியிட, இரு கோடுகளும் வெட்டிக் கொள்ளும் புள்ளி கிடைக்கும்.

எடுத்துக்காட்டு 6.33

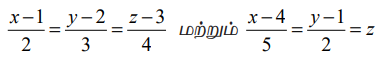என்ற கோடுகள் வெட்டும் புள்ளியைக் காண்க.

தீர்வு

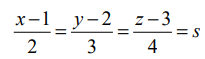(என்க). இக்கோட்டி உள்ள ஏதேனும் ஒரு புள்ளியின் வடிவம் (2s + 1, 3s+ 2, 4s+ 3) ஆகும். 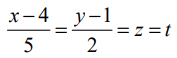(என்க). இக்கோட்டில் உள்ள ஏதேனும் புள்ளியின் வடிவம் (5t + 4, 2t+ 1, t) ஆகும்.

கொடுக்கப்பட்ட கோடுகள் வெட்டிக் கொள்ளுமானால், வெட்டும் புள்ளியில், ஒருசில s, t−ன் மதிப்புகளுக்கு,

(2s + 1, 3s + 2, 4s + 3) = (5t +4, 2t+1, t)

எனவே, 2s − 5t =3, 3s − 2t = −1 மற்றும் 4s – t = −3. இம்மூன்று சமன்பாடுகளில், முதல் இரண்டு சமன்பாடுகளின் தீர்வு காண t =−1, s =−1 எனக் கிடைக்கிறது. s மற்றும் t –ன் இம்மதிப்புகள் மூன்றாவது சமன்பாட்டை நிறைவு செய்கின்றன. எனவே, கொடுக்கப்பட்ட கோடுகள் வெட்டும் கோடுகளாகும். t அல்லது s –ன் மதிப்பினை உரிய புள்ளிகளில் பிரதியிட, கோடுகள் வெட்டும் புள்ளி (−1,−1,−1) எனக் கிடைக்கிறது.

Tags : Definition, Solved Example Problems, Solution வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள்.

12th Maths : UNIT 6 : Applications of Vector Algebra : Point of intersection of two straight lines Definition, Solved Example Problems, Solution in Tamil : 12th Standard Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் : இரு நேர்க்கோடுகள் வெட்டும் புள்ளி (Point of intersection of two straight lines) - வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் : 12 ஆம் வகுப்பு புத்தகம் கேள்விகள் மற்றும் பதில்கள்.