முப்பரிமாண வடிவக் கணிதத்தில் வெக்டர்களின் பயன்பாடு (Application of Vectors to 3−Dimensional Geometry)

முப்பரிமாண வடிவக் கணிதத்தில் வெக்டர்களின் பயன்பாடு (Application of Vectors to 3−Dimensional Geometry)

முப்பரிமாண வெளியில் நேர்க்கோடுகள் மற்றும் தளங்களைப் பற்றி கற்றறிவதில் வெக்டர்கள் ஒரு நேர்த்தியான அணுகுமுறையை வழங்குகின்றன. எல்லா நேர்க்கோடுகளும் தளங்களும் ℝ3 ன் உட்கணங்களாகும். ஒரு நேர்க்கோட்டினை சுருக்கமாகக் கோடு என்றே அழைக்கிறோம்.

ℝ3 –ல் உள்ள புள்ளிகளின் தொகுப்பு P−ல் உள்ள ஒரே கோட்டிலமையாத A,B,C எனும் ஏதேனும் மூன்று புள்ளிகளில், எவையேனும் இரு புள்ளிகளின் வழியாகச் செல்லும் கோடு P−ன் உட்கணமாக அமையுமாறு உள்ள புள்ளிகள் அமைந்துள்ள பரப்பு ஒரு தளமாகும்.

குறைந்தது ஒரு பொதுப்புள்ளியையும் மற்றும் ஒரு தளத்தில் உள்ள ஒரு புள்ளி மற்றொரு தளத்தின் மீது அமையாது என்றவாறு குறைந்த பட்சம் ஒரு புள்ளியையாவதுப் பெற்றுள்ள இரு தளங்கள் வெட்டிக் கொள்ளும் தளங்கள் எனப்படும். மிகச் சரியாக அதே புள்ளிகளைப் பெற்றுள்ள இரு தளங்கள் ஒன்றிணைந்த (ஒன்றிய) தளங்கள் எனப்படும். பொதுவான புள்ளியைப் பெறாத இரு தளங்கள் இணையான தளங்களாகும். ஆனால், அவை ஒன்றிணைந்த தளங்களாக இருக்காது. இதேபோல், வெட்டிக் கொள்ளும் இரண்டு தளங்களின் பொதுப் புள்ளிகளின் தொகுப்பு ஒரு நேர்க்கோடாகும் என அறியப்படுகிறது. இப்பாடப்பகுதியில். வெக்டர்களைப் பயன்படுத்தி நேர்க்கோடு மற்றும் தளங்களின் வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காணலாம்.

ஒரு வடிவியல் உருவின் சமன்பாட்டை அவ்வுருவின் மீதுள்ள  ஒவ்வொரு புள்ளியின் நிலை வெக்டரும் நிறைவு செய்யுமானால், அச்சமன்பாடு அவ்வடிவியல் உருவின் வெக்டர் சமன்பாடு எனப்படும். ஒரு சமன்பாடு வெக்டர் சமன்பாடாகவோ அல்லது கார்டீசியன் சமன்பாடாகவோ இருக்கலாம்.

1. ஒரு நேர்க்கோட்டின் பல்வேறு வடிவச் சமன்பாடுகள் (Different forms of equation of a straight line)

ஒரு நேர்க்கோட்டின் சமன்பாட்டைத் தனித்ததாக பின்வரும் இரு முறைகளில் காணலாம். 

• கோட்டின் மீதுள்ள ஒரு புள்ளியும், நேர்க்கோட்டின் திசையும் கொடுக்கப்படும்போது

• கோட்டின் மீதுள்ள இரு புள்ளிகள் கொடுக்கப்படும்போது

ஒரு கோட்டின் சமன்பாட்டை வெக்டர் மற்றும் கார்டீசியன் வடிவங்களில் காணலாம். ஒரு கோட்டின் மீது என்ற நிலை வெக்டரைக் கொண்ட ஏதேனும் ஒரு புள்ளி P ஆனது எடுத்துக் கொள்ளப்பட்டு, கொடுக்கப்பட்ட நிபந்தனைகளை என்ற வெக்டர் நிறைவு செய்யுமாறு ஒரு தொடர்பானது பெறப்படுகிறது. இத்தகைய தொடர்பானது கோட்டின் வெக்டர் சமன்பாடு எனப்படுகிறது. ஒரு நேர்க்கோட்டின் வெக்டர் சமன்பாட்டில் துணையலகுகள் இருக்கலாம் அல்லது இல்லாமலும் இருக்கலாம். ஒரு வெக்டர் சமன்பாடு, துணையலகுகளைப் பெற்றிருந்தால், துணையலகு வடிவ அல்லது துணையலகு வெக்டர் சமன்பாடு எனவும் துணையலகுகள் இல்லையென்றால் துணையலகு அல்லாத வடிவ அல்லது துணையலகு அல்லாத வெக்டர் சமன்பாடு எனவும் அழைக்கப்படுகிறது.

2. நேர்க்கோட்டின் மீதுள்ள ஒரு புள்ளி மற்றும் நேர்க்கோட்டின் திசை கொடுக்கப்படும் போது கோட்டின் சமன்பாடு (A point on the straight line and the direction of the straight line are given)

(a) துணையலகு வடிவ வெக்டர் சமன்பாடு (Parametric form of vector equation)

தேற்றம் 6.11

நிலை வெக்டர் எனக்கொண்ட நிலைத்த புள்ளி வழியாகச்  செல்வதும், கொடுக்கப்பட்ட –க்கு இணையாகவும் உள்ள நேர்க்கோட்டின் வெக்டர் சமன்பாடு 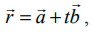இங்கு t ∈ ℝ.

நிரூபணம்

இது கொடுக்கப்பட்ட கோட்டின் துணையலகு வடிவ வெக்டர் சமன்பாடு ஆகும்.

குறிப்புரை

இக்கோட்டின் மீதுள்ள ஏதேனும் ஒரு புள்ளியின் நிலைவெக்டர் 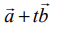ஆகும்.

(b) துணையலகு அல்லாத வெக்டர் சமன்பாடு (Non−parametric form of vector equation) 

இது கோட்டின் துணையலகு அல்லாத வடிவ வெக்டர் சமன்பாடு எனப்படும்.

(c) கார்டீசியன் சமன்பாடு (Cartesian equation)

A என்ற புள்ளியின் அச்சுத்தூரங்கள் (x1,y1,z1), P என்ற புள்ளியின் அச்சுத்தூரங்கள் (x,y,z) மற்றும் 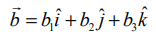என்க. பின்னர், 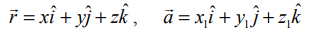மற்றும் 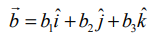எனச் சமன்பாடு (1)−ல் பிரதியிட்டு, 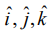ஆகியவற்றின் கெழுக்களை ஒப்பிட, நாம் பெறுவது

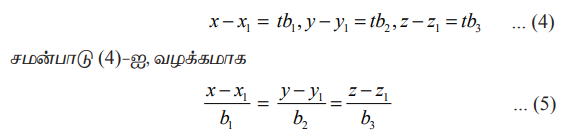
என எழுதுவோம்.

இச்சமன்பாடுகள் (x1,y1,z1) என்ற புள்ளி வழியாகச் செல்வதும் b1, b2, b3 என்ற திசை விகிதங்களைக் கொண்ட வெக்டருக்கு இணையானதுமான கோட்டின் கார்டீசியன் சமன்பாடுகள் அல்லது சமச்சீர் சமன்பாடுகள் என அழைக்கப்படுகின்றன.

குறிப்புரை

(i) நேர்க்கோடு (5)−ன் மீது உள்ள எந்தவொரு புள்ளியும் (x1 + tb1, y1 + tb2, z1 + tb3), என்ற வடிவில் இருக்கும். இங்கு t ∈ ℝ

(ii) ஒரு கோட்டின் திசைக் கொசைன்கள் அக்கோட்டின் திசை விகிதங்களின் விகிதச் சமமாகும் என்பதால், கோட்டின் திசைக் கொசைன்கள் 1, m, n எனில், நேர்க்கோட்டின் கார்டீசியன் சமன்பாடுகள்

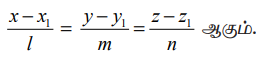
(iii) சமன்பாடு (5)−ல், b1, b2 ,b3 இவற்றில் ஒன்று அல்லது இரண்டின் மதிப்புகள் பூச்சியமாக இருந்தால், சமன்பாடுகளை நாம் பூச்சியத்தால் வகுப்பதாக பொருள்படாது (அர்த்தமாகாது). மாறாக, பகுதியில் பூச்சியத்தைக் கொண்டுள்ள சமன்பாட்டின் தொகுதியின் மதிப்பு பூச்சியத்திற்குச் சமமாகும் எனப் பொருள்படும். உதாரணமாக, b1 ≠ 0, b2 ≠ 0 மற்றும் b3 ≠ 0 எனில், 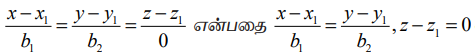  என எழுதலாம்.

(iv) x−அச்சின் திசைக் கொசைன்கள் 1,0,0 ஆகும். எனவே, x−அச்சின் சமன்பாடுகள் 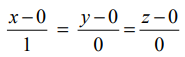அல்லது x = t, y = 0 ,z = 0, இங்கு t ∈ ℝ ஆகும். இதேபோன்று, y−அச்சு மற்றும் z−அச்சின் சமன்பாடுகள் முறையே 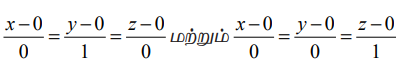ஆகும்.

3. கொடுக்கப்பட்ட இரண்டு புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டின் சமன்பாடு (Straight Line passing through two given points)

(a) துணையலகு வெக்டர் சமன்பாடு (Parametric form of vector equation)

தேற்றம் 6.12

கொடுக்கப்பட்ட நிலைவெக்டர்கள் 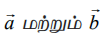கொண்ட இரு புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டின் துணையலகு வடிவ வெக்டர் சமன்பாடு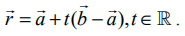

(b) துணையலகு அல்லாத வெக்டர் சமன்பாடு (Non−parametric form of vector equation) 

மேற்கண்ட சமன்பாட்டினை துணை அல்லாத வடிவ வெக்டர் சமன்பாடாக 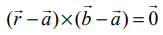  என எழுதலாம்.

(c) கார்டீசியன் சமன்பாடு (Cartesian form of equation)

A, B என்ற புள்ளிகளின் அச்சுத்தூரங்கள் முறையே (x1, y1, z1) மற்றும் (x2, y2, z2 ) என்க. P−ன் அச்சுத்தூரங்கள் (x,y,z) என்க. பின்னர் 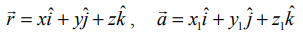மற்றும் 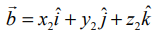எனத் தேற்றம் 6.12−ல் உள்ள சமன்பாட்டில் பிரதியிட்டு, 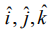ஆகியவற்றின் கெழுக்களை ஒப்பிட, x−x1 = t(x2−x1), y−y1 = t(y2,−y1), z−z1 = t(z2−z1) எனப் பெறுகிறோம். ஆகவே, (x1, y1, z1) மற்றும் (x2, y2, z2) என்ற இரு புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டின் கார்டீசியன் சமன்பாடு  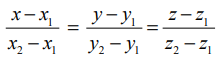 எனக் கிடைக்கிறது.

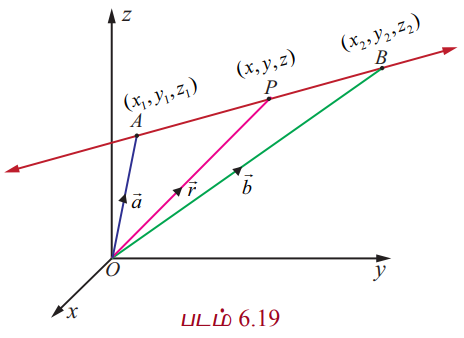
இச்சமன்பாட்டிலிருந்து (x1, y1, z1) மற்றும் (x2, y2, z2) என்ற புள்ளிகள் வழியாகச் வழியாகச் செல்லும் நேர்க்கோட்டின் திசை விகிதங்கள் x2 – x1, y2 – y1, z2 − z1 ஆகும் எனக் காண்கிறோம். மேலும் இவற்றுக்கு விகிதச் சமமமாக உள்ள ஏதேனும் மூன்று எண்கள், குறிப்பாக x1 – x2,  y1 – y2, z1 – z2 என்பவை இக்கோட்டின் திசை விகிதங்களாக அமைவதைக் காணலாம்.

எடுத்துக்காட்டு 6.24

ஒரு நேர்க்கோடு (1,2,−3) என்ற புள்ளி வழியாகச் செல்கிறது மற்றும் என்ற வெக்டருக்கு இணையாக உள்ளது எனில், அக்கோட்டின் (i) துணை அலகு வெக்டர் சமன்பாடு (ii) துணை அல்லாத வெக்டர் சமன்பாடு (iii) கார்டீசியன் சமன்பாடுகளைக் காண்க.

தீர்வு

தேவையான கோடு (1,2,−3) என்ற புள்ளி வழியாகச் செல்கிறது. ஆகவே, இப்புள்ளியின் நிலை வெக்டர் 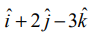ஆகும்.

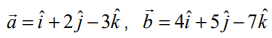என்க. பின்னர்

(i) தேவையான கோட்டின் துணை அலகு வெக்டர் சமன்பாடு 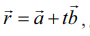இங்கு t ∈ ℝ ஆகும். எனவே,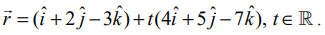

(ii) தேவையான கோட்டின் துணை அலகு அல்லாத வெக்டர் சமன்பாடு 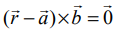ஆகும். எனவே,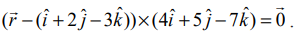

(iii) தேவையான கோட்டின் கார்டீசியன் சமன்பாடுகள் 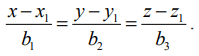இங்கு, (x1 y1 z1)  = (1,2,−3) மற்றும் தேவையான கோட்டின் திசை விகிதங்கள் 4,5,−7 என்பவற்றுக்கு விகிதச் சமமானவையாகும். எனவே, தேவையான நேர்க்கோட்டின் கார்டீசியன் சமன்பாடுகள்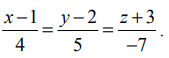 

எடுத்துக்காட்டு 6.25

ஒரு நேர்க்கோட்டின் துணையலகு வெக்டர் சமன்பாடு 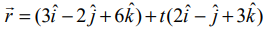எனில், அக்கோட்டின் (i) திசைக்கொசைன்கள் (ii) துணையலகு அல்லாத வெக்டர் சமன்பாடு (iii) கார்டீசியன் சமன்பாடுகள் ஆகியவற்றைக் காண்க.

தீர்வு

கொடுக்கப்பட்ட வெக்டர் சமன்பாட்டையும் 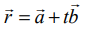என்ற கோட்டின் சமன்பாட்டையும் ஒப்பிட நமக்குக் கிடைப்பது 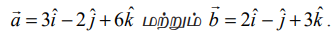எனவே,

(i) 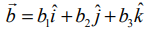  எனில், கோட்டின் திசை விகிதங்கள் b1, b2, b3 ஆகும். எனவே, கொடுக்கப்பட்ட கோட்டின் திசை விகிதங்கள் 2,−1,3 என்பவற்றுக்கு விகிதச் சமமானவையாகும். ஆகவே, கொடுக்கப்பட்ட கோட்டின் திசைக் கொசைன்கள் 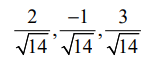ஆகும்.

(ii) கோட்டின் துணை அலகு அல்லாத வடிவ வெக்டர் சமன்பாடு 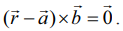எனவே,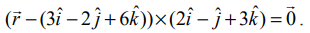

(iii) இங்கு (x1, y1, z1) = (3,−2,6) மற்றும் கோட்டின் திசை விகிதங்கள் 2,−1,3 என்பவற்றுக்கு விகிதச் சமமானவை. 

எனவே, கோட்டின் கார்டீசியன் சமன்பாடுகள் 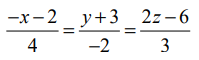  ஆகும்.

எடுத்துக்காட்டு 6.26

(–4,2,−3) என்ற புள்ளி வழிச் செல்வதும் 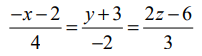  என்ற கோட்டிற்கு இணையானதுமான கோட்டின் துணையலகு வடிவ வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.

தீர்வு

கொடுக்கப்பட்ட சமன்பாடுகளை 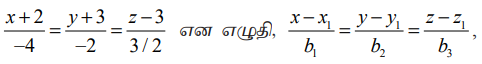உடன் ஒப்பிடக் கிடைப்பது, 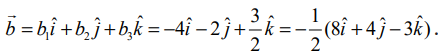இதிலிருந்து ஆனது 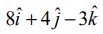  என்ற வெக்டருக்கு இணையானது எனத் தெளிவாகக் காணலாம்.

எனவே, தேவையான நேர்க்கோடு (–4,2,−3) என்ற புள்ளி வழிச் செல்வதுடன் 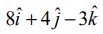என்ற வெக்டருக்கு இணையாகவும் உள்ளது. ஆதலால், தேவையான கோட்டின் துணையலகு வெக்டர் சமன்பாடு

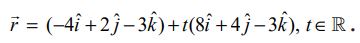
மேலும், தேவையான கோட்டின் கார்டீசியன் சமன்பாடுகள் 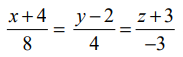  ஆகும்.

எடுத்துக்காட்டு 6.27

(−5,7,−4) மற்றும் (13,–5,2) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டின் துணையலகு வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க. மேலும், இந்த நேர்க்கோடு xy−தளத்தை வெட்டும் புள்ளியைக் காண்க.

தீர்வு

தேவையான நேர்க்கோடு (−5,7,−4) மற்றும் (13,–5,2) என்ற புள்ளிகள் வழியாகச் செல்கிறது. எனவே, இப்புள்ளிகளை இணைக்கும் கோட்டின் திசை விகிதங்கள் 18,−12,6 ஆகும். அதாவது 3,−2,1 ஆகும்.

ஆதலால், தேவையான நேர்க்கோடு 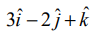என்ற வெக்டருக்கு இணையாக இருக்கும். எனவே,

• தேவையான நேர்க்கோட்டின் துணையலகு வடிவ வெக்டர் சமன்பாடு   இங்கு s, t ∈ ℝ ஆகும்.

• தேவையான கோட்டின் கார்டீசியன் சமன்பாடுகள் ஆகும்.

• இந் நேர்க்கோட்டில் உள்ள ஏதேனும் ஒரு புள்ளியின் அமைப்பு (3t −5,− 2t+ 7, t−4) அல்லது (3s + 13, − 2s − 5, s + 2)

நேர்க்கோடு xy−தளத்தை சந்திப்பதால், வெட்டும் புள்ளியின் z−அச்சுத் தொலைவு பூச்சியமாகும். எனவே, t − 4 = 0, அதாவது, t = 4 ஆகும். ஆகையால், நேர்க்கோடு xy−தளத்தை வெட்டும் புள்ளி (7,−1,0) ஆகும்.

எடுத்துக்காட்டு 6.28

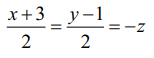என்ற நேர்க்கோடு ஆய அச்சுகளுடன் ஏற்படுத்தும் கோணங்களைக் காண்க.

தீர்வு

கொடுக்கப்பட்ட நேர்க்கோட்டுக்கு இணையாக உள்ள ஓரலகு வெக்டர் என்க. பின்னர், 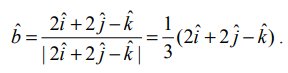 ஆகவே, −ன் திசைக் கொசைன்களின் வரையறைப்படி, நாம் பெறுவது

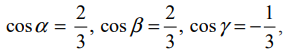
இங்கு α, β, γ என்பன முறையே மிகை x−அச்சு, மிகை y−அச்சு மற்றும் மிகை z−அச்சுக்களுடன் ஏற்படுத்தும் கோணங்கள் ஆகும். கொடுக்கப்பட்ட நேர்க்கோடு ஆய அச்சுகளுடன் ஏற்படுத்தும் கோணங்களும், முறையே ஆய அச்சுகளுடன் ஏற்படுத்தும் கோணங்களும் சமம் என்பதால் 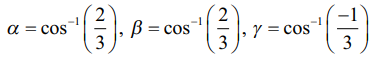எனப் பெறுகிறோம்.

4. இரண்டு நேர்க்கோடுகளுக்கு இடைப்பட்ட கோணம் (Angle between two straight lines)

(a) வெக்டர் வடிவம் (Vector form)

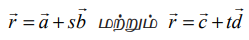என்ற இரு நேர்க்கோடுகளுக்கு இடைப்பட்ட குறுங்கோணமும் மற்றும் என்ற வெக்டர்களுக்கு இடைப்பட்ட கோணமும் ஒன்றேயாகும். ஆகையால்,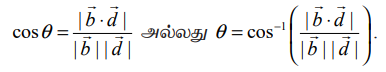

குறிப்புரை

(i) 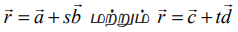  என்ற இரு கோடுகளும் இணை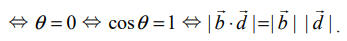 

(ii) கொடுக்கப்பட்ட 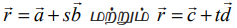 என்ற இரு கோடுகளும் இணையாக இருக்கத் தேவையானதும், மற்றும் போதுமானதுமான நிபந்தனை 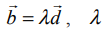ஒரு திசையிலி என்பதாகும்.

(iii) கொடுக்கப்பட்ட 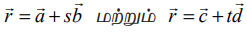என்ற இரு கோடுகளும் ஒன்றுக்கொன்று செங்குத்தானவையாக இருக்கத் தேவையானதும், மற்றும் போதுமானதுமான நிபந்தனை 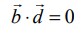என்பதாகும்.

(b) கார்டீசியன் வடிவம் (Cartesian form)

இரு நேர்க்கோடுகளின் கார்டீசியன் வடிவச் சமன்பாடுகள் 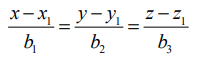மற்றும் 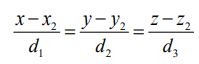எனில், இவ்விரு கோடுகளுக்கும் இடைப்பட்ட குறுங்கோணம் θ என்பது  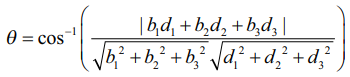ஆகும்.

குறிப்புரை

 (i) b1,b2,b3 மற்றும் d1,d2,d3 என்ற திசை விகிதங்களைக் கொண்ட கொடுக்கப்பட்ட இரு கோடுகள் இணையாக இருக்கத் தேவையானதும், மற்றும் போதுமானதுமான நிபந்தனை 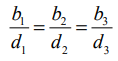  என்பதாகும்.

 (ii) b1,b2,b3 மற்றும் d1,d2,d3 என்ற திசை விகிதங்களைக் கொண்ட கொடுக்கப்பட்ட இரு நேர்க்கோடுகள் ஒன்றுக்கொன்று செங்குத்தாக இருக்கத் தேவையானதும் மற்றும், போதுமானதுமான நிபந்தனை b1d1 + b2d2 + b3d3 = 0 என்பதாகும்.

 (iii) கொடுக்கப்பட்ட இரு நேர்க்கோடுகளின் திசைக்கொசைன்கள் l1,m1,n1 மற்றும் l2,m2,n2 எனில், கொடுக்கப்பட்ட கோடுகளுக்கு இடைப்பட்ட கோணம் 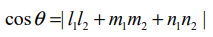ஆகும்.

எடுத்துக்காட்டு 6.29

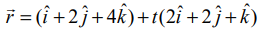என்ற கோட்டிற்கும் (5,1,4) மற்றும் (9,2,12) என்ற புள்ளிகளை இணைக்கும் கோட்டிற்கும் இடைப்பட்ட கோணம் காண்க.

தீர்வு

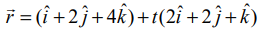என்ற கோடு 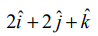என்ற வெக்டருக்கு இணையாக இருக்கும்.

(5,1,4) மற்றும் (9,2,12) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோட்டின் திசை விகிதங்கள் 4,1,8 என்பதால், இக்கோடு 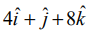  என்ற வெக்டருக்கு இணையாக இருக்கும்.

எனவே, கொடுக்கப்பட்ட இவ்விரு கோடுகளுக்கும் இடைப்பட்ட குறுங்கோணம்

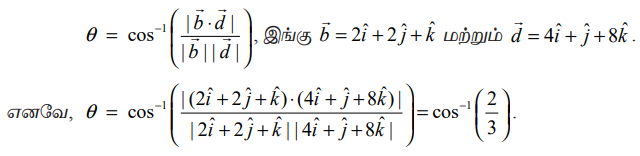
எடுத்துக்காட்டு 6.30

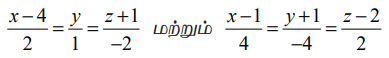என்ற இரு நேர்க்கோடுகளுக்கு இடைப்பட்ட  குறுங்கோணம் காண்க. இவ்விரு கோடுகளும் இணையானவையா அல்லது செங்குத்தானவையா எனக் காண்க.

தீர்வு

கொடுக்கப்பட்ட நேர்க்கோடுகளின் சமன்பாடுகளை 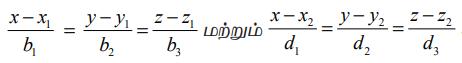ஆகியவற்றுடன் ஒப்பிட, நாம் பெறுவது (b1,b2,b3) = (2,1,−2) மற்றும் (d1,d2,d3) = (4,−4,2) எனவே, கொடுக்கப்பட்ட இரு கோடுகளுக்கும் இடைப்பட்ட குறுங்கோணம்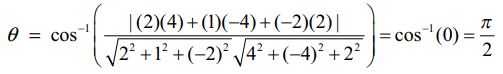

 ஆகவே, கொடுக்கப்பட்ட இரு நேர்க்கோடுகளும் செங்குத்தானவை. 

எடுத்துக்காட்டு 6.31

A(6,7,5) மற்றும் B(8,10,6) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடானது C(10,2,–5) மற்றும் D(8,3,−4) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டிற்குச் செங்குத்தானது என நிறுவுக.

தீர்வு

A(6,7,5) மற்றும் B(8,10,6) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடு 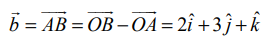என்ற வெக்டருக்கு இணையாக அமையும். மேலும் C(10,2,–5) மற்றும் D(8,3,−4) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடு 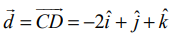என்ற வெக்டருக்கு இணையாக இருக்கும். எனவே, இவ்விரு கோடுகளுக்கு இடைப்பட்ட கோணமானது மற்றும்  ஆகியவற்றுக்கு இடைப்பட்ட கோணத்திற்குச் சமமாகும்.

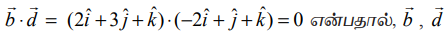என்ற வெக்டர்கள் செங்குத்தானவையாகும். எனவே, இரு நேர்க்கோடுகளும் செங்குத்தானவையாகும்.

மாற்றுமுறை

A(6,7,5) மற்றும் B(8,10,6) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோட்டின் திசை விகிதங்கள் (b1,b2,b3) = (2,3,1) ஆகும். மேலும், C(10,2,−5) மற்றும் D(8,3,−4) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோட்டின் திசை விகிதங்கள் (d1,d2,d3) = (−2,1,1) ஆகும்.

b1d1 + b2d2 + b3d3 = (2)(−2) + (3)(1) + (1)(1) = 0 என்பதால், இவ்விரு கோடுகளும் செங்குத்தானவையாகும்.

எடுத்துக்காட்டு 6.32

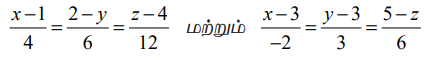என்ற கோடுகள் இணையானவை என நிறுவுக.

தீர்வு

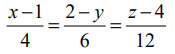என்ற கோடு 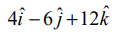என்ற வெக்டருக்கு இணையாக இருக்கும் மற்றும் 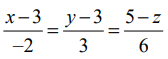என்ற கோடு 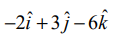என்ற வெக்டருக்கு இணையாக இருக்கும். 

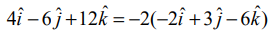என்பதால், இரு வெக்டர்களும் இணையாகும். எனவே, கொடுக்கப்பட்ட இரு நேர்க்கோடுகளும் இணையாகும்.