வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் - இரண்டு நேர்க்கோடுகளுக்கு இடைப்பட்ட கோணம் (Angle between two straight lines) | 12th Maths : UNIT 6 : Applications of Vector Algebra
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்
இரண்டு நேர்க்கோடுகளுக்கு இடைப்பட்ட கோணம் (Angle between two straight lines)
4. இரண்டு நேர்க்கோடுகளுக்கு இடைப்பட்ட கோணம் (Angle between two straight lines)
(a) வெக்டர் வடிவம் (Vector form)
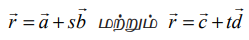 என்ற இரு நேர்க்கோடுகளுக்கு இடைப்பட்ட குறுங்கோணமும்
என்ற இரு நேர்க்கோடுகளுக்கு இடைப்பட்ட குறுங்கோணமும் ![]() மற்றும்
மற்றும் ![]() என்ற வெக்டர்களுக்கு இடைப்பட்ட கோணமும் ஒன்றேயாகும். ஆகையால்,
என்ற வெக்டர்களுக்கு இடைப்பட்ட கோணமும் ஒன்றேயாகும். ஆகையால், 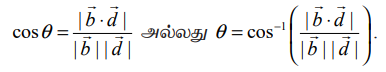
குறிப்புரை
(i) 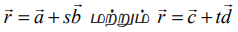 என்ற இரு கோடுகளும் இணை
என்ற இரு கோடுகளும் இணை 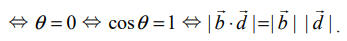
(ii) கொடுக்கப்பட்ட 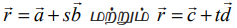 என்ற இரு கோடுகளும் இணையாக இருக்கத் தேவையானதும், மற்றும் போதுமானதுமான நிபந்தனை
என்ற இரு கோடுகளும் இணையாக இருக்கத் தேவையானதும், மற்றும் போதுமானதுமான நிபந்தனை 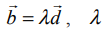 ஒரு திசையிலி என்பதாகும்.
ஒரு திசையிலி என்பதாகும்.
(iii) கொடுக்கப்பட்ட 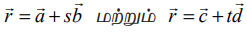 என்ற இரு கோடுகளும் ஒன்றுக்கொன்று செங்குத்தானவையாக இருக்கத் தேவையானதும், மற்றும் போதுமானதுமான நிபந்தனை
என்ற இரு கோடுகளும் ஒன்றுக்கொன்று செங்குத்தானவையாக இருக்கத் தேவையானதும், மற்றும் போதுமானதுமான நிபந்தனை 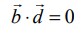 என்பதாகும்.
என்பதாகும்.
(b) கார்டீசியன் வடிவம் (Cartesian form)
இரு நேர்க்கோடுகளின் கார்டீசியன் வடிவச் சமன்பாடுகள் 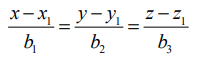 மற்றும்
மற்றும் 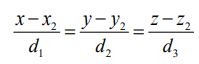 எனில், இவ்விரு கோடுகளுக்கும் இடைப்பட்ட குறுங்கோணம் θ என்பது
எனில், இவ்விரு கோடுகளுக்கும் இடைப்பட்ட குறுங்கோணம் θ என்பது 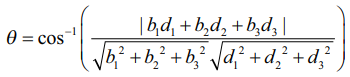 ஆகும்.
ஆகும்.
குறிப்புரை
(i) b1,b2,b3 மற்றும் d1,d2,d3 என்ற திசை விகிதங்களைக் கொண்ட கொடுக்கப்பட்ட இரு கோடுகள் இணையாக இருக்கத் தேவையானதும், மற்றும் போதுமானதுமான நிபந்தனை 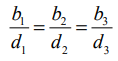 என்பதாகும்.
என்பதாகும்.
(ii) b1,b2,b3 மற்றும் d1,d2,d3 என்ற திசை விகிதங்களைக் கொண்ட கொடுக்கப்பட்ட இரு நேர்க்கோடுகள் ஒன்றுக்கொன்று செங்குத்தாக இருக்கத் தேவையானதும் மற்றும், போதுமானதுமான நிபந்தனை b1d1 + b2d2 + b3d3 = 0 என்பதாகும்.
(iii) கொடுக்கப்பட்ட இரு நேர்க்கோடுகளின் திசைக்கொசைன்கள் l1,m1,n1 மற்றும் l2,m2,n2 எனில், கொடுக்கப்பட்ட கோடுகளுக்கு இடைப்பட்ட கோணம் 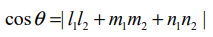 ஆகும்.
ஆகும்.
எடுத்துக்காட்டு 6.29
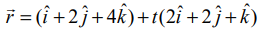 என்ற கோட்டிற்கும் (5,1,4) மற்றும் (9,2,12) என்ற புள்ளிகளை இணைக்கும் கோட்டிற்கும் இடைப்பட்ட கோணம் காண்க.
என்ற கோட்டிற்கும் (5,1,4) மற்றும் (9,2,12) என்ற புள்ளிகளை இணைக்கும் கோட்டிற்கும் இடைப்பட்ட கோணம் காண்க.
தீர்வு
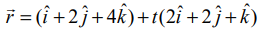 என்ற கோடு
என்ற கோடு 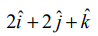 என்ற வெக்டருக்கு இணையாக இருக்கும்.
என்ற வெக்டருக்கு இணையாக இருக்கும்.
(5,1,4) மற்றும் (9,2,12) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோட்டின் திசை விகிதங்கள் 4,1,8 என்பதால், இக்கோடு 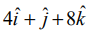 என்ற வெக்டருக்கு இணையாக இருக்கும்.
என்ற வெக்டருக்கு இணையாக இருக்கும்.
எனவே, கொடுக்கப்பட்ட இவ்விரு கோடுகளுக்கும் இடைப்பட்ட குறுங்கோணம்
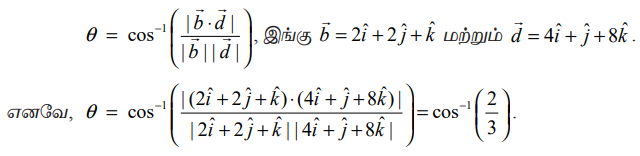
எடுத்துக்காட்டு 6.30
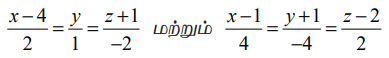 என்ற இரு நேர்க்கோடுகளுக்கு இடைப்பட்ட குறுங்கோணம் காண்க. இவ்விரு கோடுகளும் இணையானவையா அல்லது செங்குத்தானவையா எனக் காண்க.
என்ற இரு நேர்க்கோடுகளுக்கு இடைப்பட்ட குறுங்கோணம் காண்க. இவ்விரு கோடுகளும் இணையானவையா அல்லது செங்குத்தானவையா எனக் காண்க.
தீர்வு
கொடுக்கப்பட்ட நேர்க்கோடுகளின் சமன்பாடுகளை 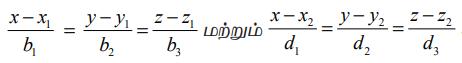 ஆகியவற்றுடன் ஒப்பிட, நாம் பெறுவது (b1,b2,b3) = (2,1,−2) மற்றும் (d1,d2,d3) = (4,−4,2) எனவே, கொடுக்கப்பட்ட இரு கோடுகளுக்கும் இடைப்பட்ட குறுங்கோணம்
ஆகியவற்றுடன் ஒப்பிட, நாம் பெறுவது (b1,b2,b3) = (2,1,−2) மற்றும் (d1,d2,d3) = (4,−4,2) எனவே, கொடுக்கப்பட்ட இரு கோடுகளுக்கும் இடைப்பட்ட குறுங்கோணம் 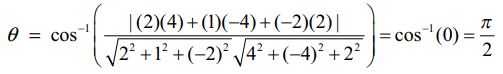
ஆகவே, கொடுக்கப்பட்ட இரு நேர்க்கோடுகளும் செங்குத்தானவை.
எடுத்துக்காட்டு 6.31
A(6,7,5) மற்றும் B(8,10,6) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடானது C(10,2,–5) மற்றும் D(8,3,−4) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டிற்குச் செங்குத்தானது என நிறுவுக.
தீர்வு
A(6,7,5) மற்றும் B(8,10,6) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடு 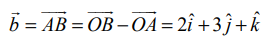 என்ற வெக்டருக்கு இணையாக அமையும். மேலும் C(10,2,–5) மற்றும் D(8,3,−4) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடு
என்ற வெக்டருக்கு இணையாக அமையும். மேலும் C(10,2,–5) மற்றும் D(8,3,−4) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடு 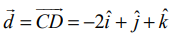 என்ற வெக்டருக்கு இணையாக இருக்கும். எனவே, இவ்விரு கோடுகளுக்கு இடைப்பட்ட கோணமானது
என்ற வெக்டருக்கு இணையாக இருக்கும். எனவே, இவ்விரு கோடுகளுக்கு இடைப்பட்ட கோணமானது ![]() மற்றும்
மற்றும் ![]() ஆகியவற்றுக்கு இடைப்பட்ட கோணத்திற்குச் சமமாகும்.
ஆகியவற்றுக்கு இடைப்பட்ட கோணத்திற்குச் சமமாகும்.
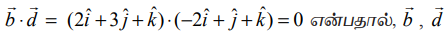 என்ற வெக்டர்கள் செங்குத்தானவையாகும். எனவே, இரு நேர்க்கோடுகளும் செங்குத்தானவையாகும்.
என்ற வெக்டர்கள் செங்குத்தானவையாகும். எனவே, இரு நேர்க்கோடுகளும் செங்குத்தானவையாகும்.
மாற்றுமுறை
A(6,7,5) மற்றும் B(8,10,6) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோட்டின் திசை விகிதங்கள் (b1,b2,b3) = (2,3,1) ஆகும். மேலும், C(10,2,−5) மற்றும் D(8,3,−4) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோட்டின் திசை விகிதங்கள் (d1,d2,d3) = (−2,1,1) ஆகும்.
b1d1 + b2d2 + b3d3 = (2)(−2) + (3)(1) + (1)(1) = 0 என்பதால், இவ்விரு கோடுகளும் செங்குத்தானவையாகும்.
எடுத்துக்காட்டு 6.32
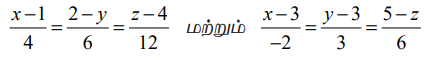 என்ற கோடுகள் இணையானவை என நிறுவுக.
என்ற கோடுகள் இணையானவை என நிறுவுக.
தீர்வு
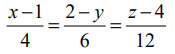 என்ற கோடு
என்ற கோடு 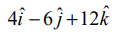 என்ற வெக்டருக்கு இணையாக இருக்கும் மற்றும்
என்ற வெக்டருக்கு இணையாக இருக்கும் மற்றும் 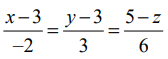 என்ற கோடு
என்ற கோடு 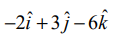 என்ற வெக்டருக்கு இணையாக இருக்கும்.
என்ற வெக்டருக்கு இணையாக இருக்கும்.
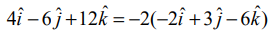 என்பதால், இரு வெக்டர்களும் இணையாகும். எனவே, கொடுக்கப்பட்ட இரு நேர்க்கோடுகளும் இணையாகும்.
என்பதால், இரு வெக்டர்களும் இணையாகும். எனவே, கொடுக்கப்பட்ட இரு நேர்க்கோடுகளும் இணையாகும்.