வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் - நேர்க்கோட்டின் மீதுள்ள ஒரு புள்ளி மற்றும் நேர்க்கோட்டின் திசை கொடுக்கப்படும் போது கோட்டின் சமன்பாடு (A point on the straight line and the direction of the straight line are given) | 12th Maths : UNIT 6 : Applications of Vector Algebra

12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்

நேர்க்கோட்டின் மீதுள்ள ஒரு புள்ளி மற்றும் நேர்க்கோட்டின் திசை கொடுக்கப்படும் போது கோட்டின் சமன்பாடு (A point on the straight line and the direction of the straight line are given)

(a) துணையலகு வடிவ வெக்டர் சமன்பாடு (Parametric form of vector equation) (b) துணையலகு அல்லாத வெக்டர் சமன்பாடு (Non−parametric form of vector equation)

2. நேர்க்கோட்டின் மீதுள்ள ஒரு புள்ளி மற்றும் நேர்க்கோட்டின் திசை கொடுக்கப்படும் போது கோட்டின் சமன்பாடு (A point on the straight line and the direction of the straight line are given)

(a) துணையலகு வடிவ வெக்டர் சமன்பாடு (Parametric form of vector equation)

தேற்றம் 6.11

நிலை வெக்டர் எனக்கொண்ட நிலைத்த புள்ளி வழியாகச் செல்வதும், கொடுக்கப்பட்ட –க்கு இணையாகவும் உள்ள நேர்க்கோட்டின் வெக்டர் சமன்பாடு 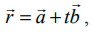இங்கு t ∈ ℝ.

நிரூபணம்

இது கொடுக்கப்பட்ட கோட்டின் துணையலகு வடிவ வெக்டர் சமன்பாடு ஆகும்.

குறிப்புரை

இக்கோட்டின் மீதுள்ள ஏதேனும் ஒரு புள்ளியின் நிலைவெக்டர் 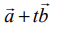ஆகும்.

(b) துணையலகு அல்லாத வெக்டர் சமன்பாடு (Non−parametric form of vector equation)

இது கோட்டின் துணையலகு அல்லாத வடிவ வெக்டர் சமன்பாடு எனப்படும்.

A என்ற புள்ளியின் அச்சுத்தூரங்கள் (x1,y1,z1), P என்ற புள்ளியின் அச்சுத்தூரங்கள் (x,y,z) மற்றும் 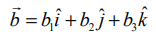என்க. பின்னர், 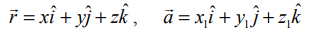மற்றும் 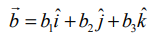எனச் சமன்பாடு (1)−ல் பிரதியிட்டு, 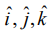ஆகியவற்றின் கெழுக்களை ஒப்பிட, நாம் பெறுவது

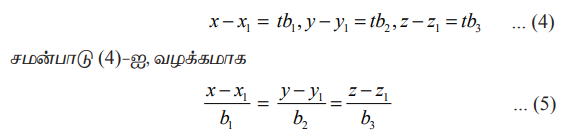
என எழுதுவோம்.

இச்சமன்பாடுகள் (x1,y1,z1) என்ற புள்ளி வழியாகச் செல்வதும் b1, b2, b3 என்ற திசை விகிதங்களைக் கொண்ட வெக்டருக்கு இணையானதுமான கோட்டின் கார்டீசியன் சமன்பாடுகள் அல்லது சமச்சீர் சமன்பாடுகள் என அழைக்கப்படுகின்றன.

குறிப்புரை

(i) நேர்க்கோடு (5)−ன் மீது உள்ள எந்தவொரு புள்ளியும் (x1 + tb1, y1 + tb2, z1 + tb3), என்ற வடிவில் இருக்கும். இங்கு t ∈ ℝ

(ii) ஒரு கோட்டின் திசைக் கொசைன்கள் அக்கோட்டின் திசை விகிதங்களின் விகிதச் சமமாகும் என்பதால், கோட்டின் திசைக் கொசைன்கள் 1, m, n எனில், நேர்க்கோட்டின் கார்டீசியன் சமன்பாடுகள்

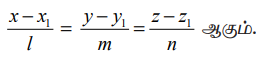
(iii) சமன்பாடு (5)−ல், b1, b2 ,b3 இவற்றில் ஒன்று அல்லது இரண்டின் மதிப்புகள் பூச்சியமாக இருந்தால், சமன்பாடுகளை நாம் பூச்சியத்தால் வகுப்பதாக பொருள்படாது (அர்த்தமாகாது). மாறாக, பகுதியில் பூச்சியத்தைக் கொண்டுள்ள சமன்பாட்டின் தொகுதியின் மதிப்பு பூச்சியத்திற்குச் சமமாகும் எனப் பொருள்படும். உதாரணமாக, b1 ≠ 0, b2 ≠ 0 மற்றும் b3 ≠ 0 எனில், 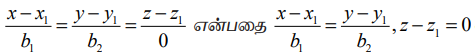என எழுதலாம்.

(iv) x−அச்சின் திசைக் கொசைன்கள் 1,0,0 ஆகும். எனவே, x−அச்சின் சமன்பாடுகள் 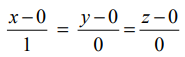அல்லது x = t, y = 0 ,z = 0, இங்கு t ∈ ℝ ஆகும். இதேபோன்று, y−அச்சு மற்றும் z−அச்சின் சமன்பாடுகள் முறையே 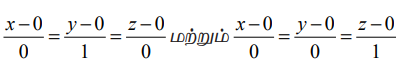ஆகும்.

Tags : Application of Vectors to 3-Dimensional Geometry வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்.

12th Maths : UNIT 6 : Applications of Vector Algebra : A point on the straight line and the direction of the straight line Application of Vectors to 3-Dimensional Geometry in Tamil : 12th Standard Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் : நேர்க்கோட்டின் மீதுள்ள ஒரு புள்ளி மற்றும் நேர்க்கோட்டின் திசை கொடுக்கப்படும் போது கோட்டின் சமன்பாடு (A point on the straight line and the direction of the straight line are given) - வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் : 12 ஆம் வகுப்பு புத்தகம் கேள்விகள் மற்றும் பதில்கள்.