மட்டு மதிப்பு

மட்டு மதிப்பு (Absolute Value) 

1. வரையறை மற்றும் பண்புகள் (Definition and Properties)

ℝ-ல் உள்ள ஒவ்வொரு உறுப்பும் எண்கோட்டில் உள்ள ஒவ்வொரு புள்ளியோடு ஒழுங்கு வரிசையில் ஒன்றுக்கு ஒன்று தொடர்புடையவை என்பதைக் கண்டோம். x ∈ ℝ எனில், x மற்றும் – x ஆகியவை 0-லிருந்து சமதூரத்தில் அமைந்துள்ளன. எண்கோட்டில், a ∈ ℝ-க்கும் 0-க்கும் a-க்கும் இடைப்பட்ட தொலைவு a-ன் மட்டு மதிப்பு (absolute value) எனப்படும். மேலும், இதனை |a| எனக் குறிப்பிடலாம்.

எனவே எந்த ஒரு x ∈ ℝ-க்கும்

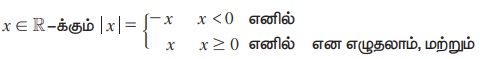
|•| ஆனது ℝ-லிருந்து [0, ∞)-க்கு மேற்கோர்த்தல் சார்பாக வரையறை செய்கிறது. இதன் வரைபடம் முதல் இயலில் கண்டோம்.

/

2. மட்டு மதிப்புகளை உடைய சமன்பாடுகள் (Equations involving absolute values)

ஒரு சமன்பாடு அல்லது அசமன்பாட்டின் தீர்வு a என்ற மெய்யெண் எனில், அக்கூற்றில் மாறிக்குப் பதிலாக a ஐப் பிரதியிட அக்கூற்று உண்மையாக வேண்டும்.

அடுத்ததாக, மட்டு மதிப்புகளைத் தன்னகத்தே கொண்ட சமன்பாடுகளின் தீர்வுகளைக் காண்போம்.

எடுத்துக்காட்டு 2.1 |2x – 17| = 3-ன் தீர்வு காண்க.

தீர்வு:

|2x – 17| = 3 எனில் 2x – 17 = ± 3 

அதாவது, x = 10 அல்லது x = 7

எடுத்துக்காட்டு 2.2  3|x - 2 |+ 7 = 19-ன் தீர்வு காண்க.

தீர்வு:

3|x - 2| + 7 = 19 

மேலும், |x - 2| = 19 - 7 / 3 = 4

எனவே, x – 2 = 4 அல்லது  x - 2 = - 4

அதாவது, தீர்வு x = - 2 மற்றும் x = 6

எடுத்துக்காட்டு 2.3 தீர்வு காண்க : |2 x – 3| = | x - 5|. 

தீர்வு:

|u| = |v| எனில், தேவையானதும் மற்றும் போதுமானதும் என்னவென்றால் u = v அல்லது u = - v ஆகும். எனவே, |2x – 3| = |x – 5| என்பது 2x – 3 = x – 5 அல்லது 2x – 3 = 5 – x. இதன் தீர்வு, x = - 2 மற்றும் x = 8/3.

3. மட்டு மதிப்புகளுக்கான சில முடிவுகள் (Some Results for Absolute Value)

(i) x,y ∈ ℝ, Iy +x | = |x - y | எனில் xy = 0 

(ii) x,y ∈ ℝ,  எனில் | xy| = |x| |y| 

(iii) x,y ∈ ℝ, y ≠ 0 எனில் |x/y| =|x|/|y|

(iv) x,y ∈ ℝ, எனில் |x + y| ≤ |x|+|y|.

4. மட்டு மதிப்புகளுடைய அசமன்பாடுகள் (Inequalities involving absolute values)

இங்கு மட்டு மதிப்புகளுடைய அசமன்பாடுகளின் தீர்வு காணுதலைக் காண்போம். முதலில் மிகவும் எளிய அசமன்பாடுகளான (i) |x|<r மற்றும் (ii) | x | > r போன்றவற்றைக் காண்போம்.

(i) |x| < r எனில், தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனை -r <x <r என நாம் நிறுவுவோம். | x | > 0 என்பதால் r > 0 என குறிக்கலாம். x-ன் குறியீட்டினைப் பொறுத்து இரண்டு நிலைகள் உள்ளன.

நிலை 1

x ≥ 0, எனில் |x| = x. எனவே, |x| < r ⇒ x <r.

நிலை 2

x < 0, எனில் |x |= -x. எனவே, |x| < r ⇒ -x <r அதாவது, x > - r.

|x| < r-க்குத் தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனை -r < x < r அல்லது x ∈ ( - r,r ) ஆகும்.

(ii) |x| > r என்பதற்கு தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனை x < -r அல்லது x > r என நிறுவுவோம். 

|x| > r என்க. r < 0 எனில், ஒவ்வொரு x ∈ R, இந்த அசமன்பாட்டை நிறைவு செய்யும்.

 r ≥ 0, எனில் இரண்டு நிலைகள் உண்டு.

நிலை 1

x  ≥ 0 எனில் |x| = x > r

நிலை 2

x < 0, எனில் |x| = − x > r அதாவது, x < - r

எனவே, |x| > r-க்குத் தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனை x < - r அல்லது x >r அதாவது x ∈ (– ∞, - r) ∪ (r, ∞) ஆகும்.

குறிப்புரை :

(i) a ∈ ℝ மற்றும் |x - a| ≤ r-க்குத் தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனை –r ≤ x – a ≤ r ஆகும். அதாவது, x ∈ [a-r, a+r] 

(ii) a ∈ ℝஎனில், |x - a| ≥ r என்பதனை x – a ≤ - r அல்லது x - a ≥ r என எழுதலாம். இதற்குத் தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனை x ∈ (- ∞, a-r] ∪ [a+r, ∞) ஆகும்.

எடுத்துக்காட்டு 2.4 தீர்க்க: |x - 9| < 2

தீர்வு:

|x-9| < 2 என்பது -2 < x-9 < 2 ஆகும். அதாவது, 7 < x < 11.

எடுத்துக்காட்டு 2.5  தீர்க்க: | -2 /x -4 | >1, x ≠ 4.

தீர்வு:

கொடுக்கப்பட்ட அசமன்பாட்டிலிருந்து 2 >| x- 4 | எனக் கிடைக்கும். 

அதாவது, – 2 <x - 4 < 2 மற்றும் x ≠ 4.

மேலும், 4 ஐக் கூட்ட 2 < x < 6 மற்றும் x ≠ 4. அதாவது, (2, 4) ∪ (4, 6) என்பது தீர்வு ஆகும்.

பயிற்சி 2.2

1. தீர்வு காண்க.

(i) |3 – x | < 7.

(ii) |4x - 5 | ≥ - 2.

(iii) |3 – 3/4x | ≤ 1/4. 

(iv) |x| - 10 < - 3 

2. 1/|2x-1| < 6-க்குத் தீர்வு கண்டு, தீர்வை இடைவெளிக் குறியீட்டில் எழுதுக.

3. - 3|x| + 5 ≤ - 2-க்குத் தீர்வு கண்டு, தீர்வை எண்கோட்டில் குறிக்க 

4. 2|x + 1|- 6 ≤ 7-க்குத் தீர்வு கண்டு, தீர்வை எண்கோட்டில் குறிக்க. 

5. தீர்க்க. 1/5 |10x - 2| < 1 

6. தீர்க்க : |5x - 12| < - 2.