இருபடிச் சார்புகள்

இருபடிச் சார்புகள் (Quadratic Functions)

Z ∈ ℝ மற்றும் n ∈ ℕ-க்கு zn = z z z... z (n-முறைகள்) என்பதை முந்தைய வகுப்புகளில் படித்துள்ளோம்.

P(x) = ax2 + bx + c, (இங்கு, a,b,c ∈ R என்பன மாறிலிகள் மற்றும் a ≠ 0) என்ற வடிவில் உள்ள சார்பு இருபடிச் சார்பு என்றழைக்கப்படுகிறது. t ∈ R-க்கு, P(t) = 0 எனில், t என்பது P(x)-ன் ஒரு பூஜ்ஜியமாகும்.

1. இருபடி சூத்திரம் (Quadratic Formula)

பொதுவாக, இருபடிச் சார்பு P(x) = ax2 + bx + c-ஐ a(x - k)2 + d என எழுத இயலுமா? இயலும். இதனை "வர்க்கத்தை நிறைவு செய்தல்" (completing the square) என்ற முறையில் கீழ்க்கண்டவாறு எழுதலாம்.

P(x)  =ax2 + bx + c

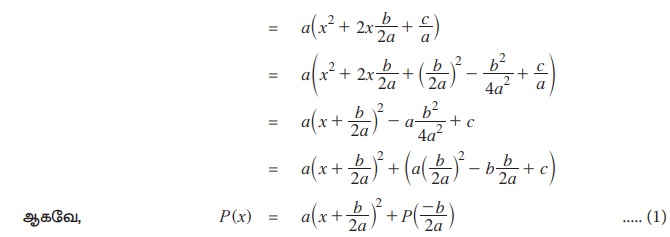
தற்போது, P(x) = 0 எனக் கொள்ளும்போது, வளைவரை P(x)-ன் x வெட்டுத்துண்டு கிடைக்கும். 

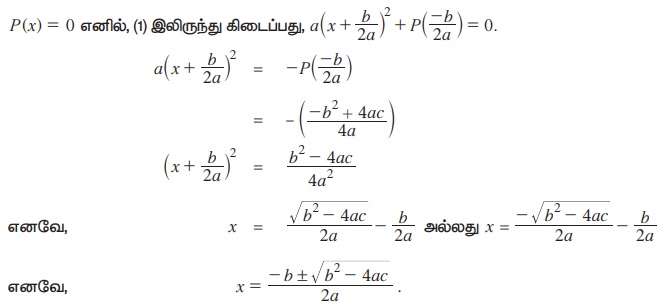
இதனை இருபடிச் சூத்திரம் (quadratic formula) என்போம்.

குறிப்புரை

(i) u ≥ 0 -க்கு மட்டும் √u ஒரு மெய்யெண் என வரையறுக்கப்படும். 

(ii) √u என எழுதினால் அது ஒரு குறையற்ற மிகை எண்ணினைக் குறிக்கும்.

b2 – 4ac > 0 எனில், P(x) = 0 -க்கு வெவ்வேறான இரு மெய்யெண்கள் தீர்வாகும். 

b2 - 4ac = 0 எனில், இரு சமமான மெய்யெண்கள் தீர்வாகும். 

மேலும், b2 – 4ac < 0 எனில், மெய் மூலங்கள் இல்லை . 

எனவே, b2 - 4ac > 0 எனில், x அச்சை இரு புள்ளிகளில் வளைவரை வெட்டும். 

b2 - 4ac = 0 எனில், வளைவரை x அச்சை ஒரு புள்ளியில் மட்டும் தொடும். 

b2 – 4ac < 0 எனில், வளைவரை x அச்சை வெட்டாது.

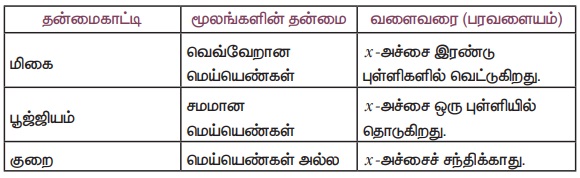
எனவே, P(x) = ax + bx + c என்ற இருபடிச் சார்பின் தன்மைகாட்டி (discriminant) D = b2- 4ac என்கிறோம்.

குறிப்பு: (i) α மற்றும் β ஆகியவை ax2 + bx + c = 0-ன் மூலங்கள் எனில் α + β  = - b/a மற்றும்  αβ = c/a ஆகும்.

(ii) தன்மைகாட்டி b2 – 4ac ஒரு குறை எண் எனில் இருபடிச் சமன்பாடு ax2+ bx + c = 0 - க்கு மெய்யெண் மூலம் இல்லை. இங்கு, கற்பனை எண்களே மூலங்களாகும்.

அவை, 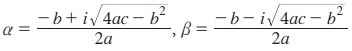 இங்கு, i2 = -1 

(இதனைப் பற்றி அடுத்த வகுப்பில் படிப்போம்) 

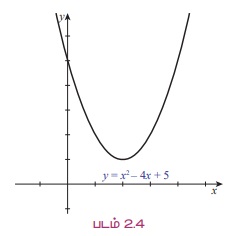
(iii) எடுத்துக்காட்டாக, y = x2 - 4x + 5 (படம் 2.4) என்ற வரைபடத்தைப் பார்க்கலாம். இந்த வரைபடம் x- அச்சை வெட்டாததால், x2 - 4x + 5 = 0 -க்கு மெய்யெண்கள் தீர்வாக அமையாது.

(iv) இரு படி சமன்பாட்டின் மூலங்களின் தன்மையை D = b2 – 4ac என்ற தன்மைகாட்டி மூலம் விவரிக்கும் அட்டவணை கீழே கொடுக்கப்பட்டுள்ளது.

எடுத்துக்காட்டு 2.10  x2 - px + q = 0 என்ற சமன்பாட்டின் மூலங்கள் a மற்றும் b எனில், 1/a+1/b-ன் மதிப்பினைக் காண்க.

தீர்வு:

a மற்றும் b ஆகியவை x2 – px + q = 0 என்ற சமன்பாட்டின் மூலங்கள். அவற்றின் கூடுதல் a + b = p மற்றும் ab = q ஆகும்.

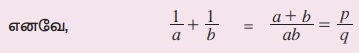
எடுத்துக்காட்டு 2.11 இருபடிச் சமன்பாடு x2 – ax + a + 2 = 0 -ன் மூலங்கள் சமம் எனில் a-ன் அனைத்து மதிப்புகளையும் காண்க. 

தீர்வு:

x2 - ax + a + 2 = 0 - ன் மூலங்கள் சமம் எனக் கொடுக்கப்பட்டுள்ளது. எனவே, தன்மைகாட்டியின் மதிப்பு பூஜ்ஜியமாகும். 

ஆகவே,   D = b2 - 4ac = a2 - 4a- 8 = 0 

எனவே,    a = 4 ± √48 / 2 

அதாவது,   a = 2 + √12, 2 - √12.

எடுத்துக்காட்டு 2.12 x2 + |x - 1| = 1 -ன் தீர்வுகளின் எண்ணிக்கையைக் காண்க. 

தீர்வு:

நிலை (1) 

x ≥ 1 எனில், | x – 1| = x - 1. 

எனவே, கொடுக்கப்பட்ட சமன்பாடு x2 + x - 2 = 0. 

காரணிப்படுத்த கிடைப்பது, (x + 2) (x - 1) = 0 ⇒ x = - 2 அல்லது 1. 

ஆனால், x ≥ 1 எனவே, x = 1. 

நிலை (2) 

x < 1 எனில், | x – 1 | = 1 – x. 

எனவே, கொடுக்கப்பட்ட சமன்பாடு x2 + 1 – x = 1.

எனவே , x (x - 1) = 0 ⇒ x = 0 அல்லது x = 1.

ஆனால் x < 1, எனவே, x = 0. 

எனவே, தீர்வுக் கணம் {0, 1} ஆகும். எனவே, இச்சமன்பாட்டிற்கு இரண்டு தீர்வுகள் உண்டு.

பயிற்சி 2.4

1. 7 மற்றும் –3 ஆகிய மூலங்களையுடைய இருபடிச் சமன்பாட்டைக் காண்க. 

2. ஒரு இருபடிக் கோவையின் ஒரு பூஜ்ஜியம் 1 + √5. மேலும், p(1) = 2 எனில், அந்த இருபடிக் கோவையைக் காண்க. 

3. x2 + √2x + 3 = 0 என்ற இருபடிச் சமன்பாட்டின் மூலங்கள் α மற்றும் β எனில், பூஜ்ஜியங்கள் 1/α மற்றும் 1/β உடைய இருபடிக் கோவையைக் காண்க 

4. k (x - 1)2 = 5x - 7 என்பதன் ஒரு மூலம் மற்றதன் இருமடங்கு எனில், k = 2 அல்லது - 25 எனக் காண்க. 

5. 2x2 – (a + 1)x + a - 1 = 0 -ன் மூலங்களுக்கிடையே உள்ள வேறுபாடும், அவைகளின் பெருக்கற்பலனும் சமம் எனில், a = 2 என நிறுவுக.

6. ax2 + bx + c = 0 -ன் ஒரு மூலம் 

(i) மற்றொரு மூலத்தின் மாற்று குறியீடு 

(ii) மற்றொரு மூலத்தைப் போல் மூன்று மடங்கு 

(iii) மற்றொரு மூலத்தின் தலைகீழி ஆக இருக்கக் கட்டுப்பாடுகளைக் காண்க. 

7. x2- ax + b = 0 மற்றும் x2 - ex + f = 0 ஆகிய சமன்பாடுகளுக்கு ஒரு பொதுவான மூலம் உள்ளது. மேலும், இரண்டாம் சமன்பாட்டிற்குச் சமமான மூலங்கள் உண்டு எனில், ae = 2(b + f) என நிறுவுக. 

8. (i) -x2 + 3x + 1 = 0 (ii) 4x2 - x - 2 = 0 (iii) 9x2 + 5x = 0 ஆகியவற்றின் மூலங்களின் தன்மையைக் காண்க. 

9. வரைபடம் வரையாமல் (i) y = x2 + x + 2, (ii) y = x2 - 3x - 7, (iii) y = x + 6x + 9 ஆகியவை x - அச்சை வெட்டுமா எனச் சோதித்தறியவும். மேலும் வெட்டும் புள்ளிகளின் எண்ணிக்கையைக் காண்க. 

10. f(x) = x2 + 5x + 4 -ஐ வர்க்கங்களின் கூடுதலாக எழுதுக. 

2. இருபடி அசமன்பாடுகள் (Quadratic Inequalities) 

இங்கு, ax2 + bx + c < 0 அல்லது ax2 + bx + c > 0 ஆகிய அசமன்பாடுகளுக்கு தீர்வு காணலாம்.

இருபடி அசமன்பாடுகளைத் தீர்வு காணப் படி நிலைகள்

(i) ax2 + bx + c = 0-க்குத் தீர்வு காண வேண்டும். 

(ii) மெய்யெண்களில் தீர்வு இல்லை எனில், மேலே உள்ளவற்றில் ஒரு அசமன்பாடு அனைத்து x ∈ ℝ-க்கும் உண்மையாகும். 

(iii) மெய்யெண்களில் தீர்வு உண்டு எனில், அது மாறுநிலைப் புள்ளிகளாகும் (critical point). அப்புள்ளிகளை எண்கோட்டில் குறித்தல் வேண்டும். 

(iv) இந்த மாறுநிலைப் புள்ளிகள் எண்கோட்டை பொது உறுப்புகளற்ற இடைவெளிகளாகப் பிரிக்கின்றன. (ஒரே ஒரு மாறுநிலைப் புள்ளி இருக்கவும் வாய்ப்புள்ளது) 

(v) ஒவ்வொரு இடைவெளியிலும் ஏதேனும் ஒரு புள்ளியை எடுத்துக் கொள்ள வேண்டும். 

(vi) அப்புள்ளிகளை அசமன்பாட்டில் உள்ள கோவையில் பிரதியிடவேண்டும்.

(vii) அசமன்பாட்டை நிறைவு செய்யும் இடைவெளியைக் காணவும்.

எடுத்துக்காட்டு 2.13 தீர்க்க: 3x2 + 5x - 2 ≤ 0 

தீர்வு:

இருபடிக் கோவையைக் காரணிப்படுத்த, 3(x + 2)(x- 1/3 ) ≤ 0 எனக் கிடைக்கும். ஒரு எண்கோட்டில் மாறுநிலைப் புள்ளிகளான -2 மற்றும் -1/3 (படம் 2.5) ஆகியவற்றைக் குறிக்கவும். ஒவ்வொரு இடைவெளியிலும் (x + 2)(x – 1/3)-ன் மிகைத் தன்மையைச் சோதிக்கவும். அவ்விடைவெளியில் ஏதேனும் ஒரு புள்ளியை எடுத்துக்கொள்க. கிடைக்கும் விடையின் குறியீடு என்னவோ, அதுவே இவ்விடைவெளியில் உள்ள அனைத்துப் புள்ளிகளையும் பிரதியிடக் கிடைக்கும் விடைகளின் குறியீடாகும். (இல்லையெனில், இந்த இடைவெளியில் மற்றொரு மாறுநிலைப்புள்ளி இருப்பதாகும்) இதைக் கீழ்க்கண்ட அட்டவணையின் மூலம் எளிதில் புரிந்துகொள்ளலாம்.

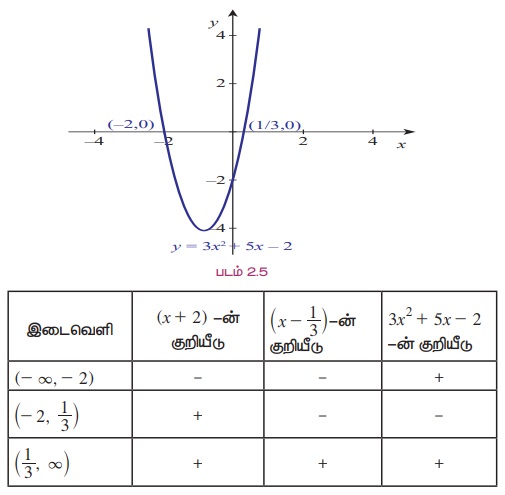
எனவே, அசமன்பாடு நிறைவு செய்யும் இடைவெளி [- 2, 1/3] ஆகும்.

எடுத்துக்காட்டு 2.14 தீர்க்க: √x + 14 < x + 2. 

தீர்வு:

√x + 14 வரையறுக்கப்பட x + 14 > 0 என இருத்தல் வேண்டும்.

x ≥ - 14 எனவே, x + 2 > 0, அதாவது x > - 2.

மேலும், (x + 14) < (x + 2)2. அதாவது, x2 + 3x – 10 > 0 எனவே, (x + 5) (x - 2) > 0.

X = -5 மற்றும் x = 2 ஆகிய மாறுநிலைப் புள்ளிகளைக் கொண்டு எண்கோட்டில் இடைவெளிகளை உருவாக்கி, அவற்றிலிருந்து புள்ளிகளைப் பிரதியிடக் கிடைக்கும் தீர்வு x < - 5 மற்றும் x > 2 ஆகும். x ≥ - 2 என்பதால் அவற்றின் தீர்வு x > 2 ஆகும்.

எடுத்துக்காட்டு 2.15  √6 - 4x -x2 = x + 4 என்ற சமன்பாட்டைத் தீர்க்க. 

தீர்வு: 

கொடுக்கப்பட்ட சமன்பாடு (x + 4) > 0 மற்றும் 6 - 4x - x2 = (x + 4)2 என்பதற்கு சமானமாகும். 

எனவே, x >- 4 மற்றும் x + 6x + 5 = 0. 

இதனைத் தீர்க்கக் கிடைப்பது, x = - 1, - 5

ஆனால், x = -1 மட்டும் இரண்டு நிபந்தனைகளையும் நிறைவு செய்கிறது. எனவே, x = -1 ஒரு தீர்வு ஆகும்.

பயிற்சி 2.5

1. தீர்வு காண்க: 2x2 + x – 15 ≤ 0. 

2. தீர்வு காண்க : - x2 + 3x- 2 ≥ 0.