அடுக்குகளும் படி மூலங்களும்

அடுக்குகளும் படி மூலங்களும் (Exponents and Radicals)

முதலில் அடுக்குகளைப் பற்றி காண்போம்.

1. அடுக்குகள் (Exponents)

n ∈ ℕ, a ∈ ℝ, எனும்போது, an = a. a … a (n முறைகள்) ஆகும். m ஒரு குறை முழு எண் மற்றும் மெய்யெண் a ≠ 0 எனில், am = 1/a-m

எந்தவொரு a ≠ 0-க்கு a/a = a1-1= a0 = 1 ஆகும். 

கீழ்க்காணும் பண்புகளை எளிதில் அறியலாம்.

அடுக்குகளின் பண்புகள் (Properties of Exponents)

i. m,n ∈ Z மேலும், a ≠ 0 எனில், am an = am+n

ii. m,n ∈ Z மேலும், a ≠ 0 எனில், am/an = am-n

2. படிமூலங்கள் (Radicals)

கேள்வி:

a≠ 0 எனில், r ∈ Q-க்கு ar -ஐ வரையறுக்க இயலுமா?

r = 1/n, n ∈ ℕ என்ற வகையைக் காண்போம்.

y = a1/n என்று இருக்குமாறு ஒரு மெய்யெண் y ∈ ℝ என இருந்தால், yn = a எனக் கிடைக்கும்.

இப்பண்பு y = xn-ன் நேர்மாறு சார்பு காணப் பயன்படுகிறது. இன்னும் தெளிவு பெறக் கீழ்க்கண்ட சார்புகளின் வரைபடங்களைக் காண்போம். 

(i) f(x) = x2n, n ∈ ℕ

(ii) g(x) = x2n+1, n ∈ ℕ

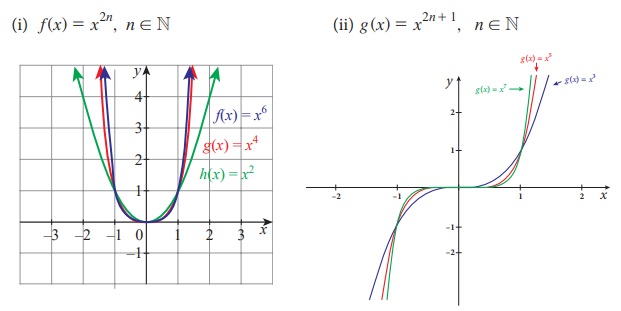
மேலே உள்ள படங்களிலிருந்து, g:ℝ→ℝ, g(x) = x2n+1 மற்றும் n ∈ ℕ ஆனது ஒன்றுக்கொன்று மற்றும் மேற்கோர்த்தல் சார்பு ஆகும். எனவே, ℝ -லிருந்து ℝ -க்கு நேர்மாறு சார்பு உண்டு. ஆனால், f: ℝ → [0,∞), f(x) = x2n, n ∈ ℕ, ஒரு மேற்கோர்த்தல் சார்பாகும், ஆனால் ஒன்றுக்கொன்றான சார்பாகாது. இருந்தபோதிலும், சார்பகத்தை [0, ∞) எனக் கட்டுப்படுத்தப்படும்போது f ஆனது இருபுறச் சார்பு ஆகும். இது ஒரு மெய்யெண்ணின் 1 படிமூலங்கள் காணப் பயன்படுகிறது. இதற்கு இரு நிலைகள் உள்ளன. 

நிலை 1: n ஒரு இரட்டைப் படை எண் என்க. 

a <0 எனில், yn = a என்பது அர்த்தமற்றதாகும். எனவே, a <0 எனில், y-ன் மதிப்பு எதுவும் இல்லை . 

a > 0 என்க. xn = a-ன் தீர்வு y எனில், - y என்பதும் xn= a-ன் தீர்வு ஆகும். 

நிலை 2: n ஒரு ஒற்றைப்படை எண் என்க. 

இந்நிலை, நிலை 1 ஐப் போல் இல்லை. 

y ∈ ℝ-க்கு y = xn என்றிருக்குமாறு ஒருமைத் தன்மையுடைய x ∈ ℝ இருக்கும். 

மேலே உள்ள நிலைகளின் அடிப்படையில் படிமூலங்களை கீழ்க்கண்டவாறு வரையறுக்கலாம்.

வரையறை 2.2 

(i) n ∈ ℕ, n ஓர் இரட்டைப்படை எண் மற்றும் b >0-க்கு an = b என்றிருக்குமாறு ஒருமைத் தன்மையுடைய a > 0 என இருக்கும். 

(ii) n ∈ ℕ, n ஓர் ஒற்றைப்படை எண் மற்றும் b ∈ ℝ -க்கு an = b என்றிருக்குமாறு ஒருமைத் தன்மையுடைய a ∈ ℝ என இருக்கும்.

இரு வகைகளிலும் a-ஐ b-ன் n படி மூலம் என அழைக்கலாம். மேலும், இதனை b1/n அல்லது n √ b எனக் குறிக்கலாம்.

குறிப்பு: (i) n = 2 எனில், n படி மூலம் வர்க்க மூலம் எனப்படும். n = 3 எனில், அது முப்படி மூலமாகும். 

(ii) x2 = a2 என்ற சமன்பாட்டிற்கு x = a மற்றும் x =-a ஆகிய இரண்டு தீர்வுகள் உள்ளன. ஆனால், √a2 = |a| ஆகும். 

(iii) ஒவ்வொரு தனி உறுப்புகளும் வரையறுக்கப்பட்டிருப்பின் மேலே கொடுக்கப்பட்ட அடுக்குகளின் பண்புகள் படிமூலங்களுக்கும் பொருந்தும். 

(iv) மேலும், n ∈ ℕ மற்றும் a ≠ 0 எனில், 

எடுத்துக்காட்டாக,

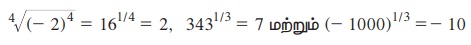
எந்தவொரு மெய்யெண் r = m/n, m ∈ Z, n ∈ ℕ, மேலும், (m,n)-ன் மீ.பொ.வ.=1 மற்றும் a > 0. எனில், ar = am/n = (a1/n)m என வரையறுக்கலாம்.

எடுத்துக்காட்டாக, 493/2 = (491/2)3 = 73 = 343. ஆனால், (-49)3/2-க்கு மெய்யெண்கள் அமைப்பில் அர்த்தமற்றது. ஏனெனில், x2 = (-49)3 -ஐ நிறைவு செய்யும் மெய்யெண் இல்லை.

3. படிக்குறி சார்புகள் அல்லது அடுக்குச் சார்புகள் (Exponential Functions)

x ∈ ℝ மற்றும் எந்தவொரு a > 0-க்கும் ax ஐ வரையறுக்கலாம். a = 1 எனில், 1x = 1 என வரையறுக்கலாம். எனவே, ax, x ∈ ℝ மற்றும் 0 < a ≠ 1 என்னும்போது ax ஐ கருத்தில் கொள்ளலாம். இங்கு, ax என்பது அடிமானம் a உடைய படிக்குறிச் சார்பாகும். a < 0 மற்றும் x = 1/m, m ∈ ℕ, ஒரு இரட்டைப்படை எனில், ax வரையறுக்கப்படவில்லை. ஆகையால், a > 0 எனக் கட்டுப்படுத்துகிறோம். மேலும், x ∈ ℝ-க்கு ax > 0.

படிக்குறிச் சார்பின் பண்புகள் (Properties of Exponential Function)

அனைத்து a,b > 0 மற்றும் a ≠ 1 ≠ b -க்கு

(i) ax+y = axay அனைத்து x,y ∈ ℝ 

(ii) ax/ay = ax-y அனைத்து x, y ∈ ℝ

(iii) (ax)y = axy அனைத்து x,y ∈ ℝ

(iv) (ab)x = axbx அனைத்து x,y ∈ ℝ

(v) ax = 1 ↔ x = 0 

1. f(x) = ax, x ∈ ℝ, a = 2

இப்பொழுது, f(x) = 2x, x∈ℝ. f ஒரு ஒன்றுக்கொன்றான மற்றும் மேற்கோர்த்தல் சார்பு என நிரூபிப்போம்.

ஏதேனும் u, v ∈ ℝ -க்கு f(u) = f(v) என்க. எனவே , 2u= 2v ⇒2u/2v = 1 ⇒ 2u-v= 1.

எனவே, u - v = 0 ⇒ u = v. ஆகையால், f ஒரு ஒன்றுக்கொன்றான சார்பாகும்.

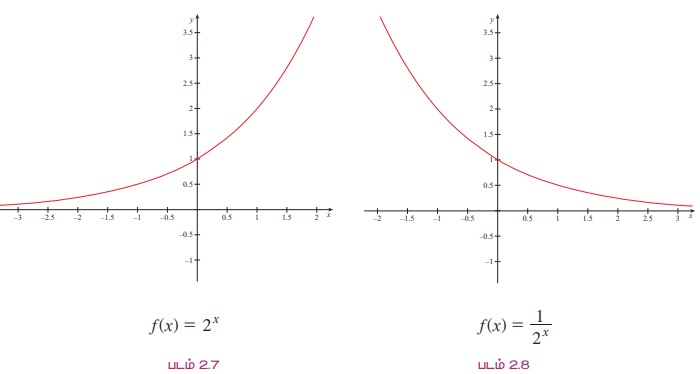
வரைபடத்திலிருந்து x அதிகரிக்கும்போது f(x)= 2x-ன் மதிப்பும் அதிகரிக்கிறது என்பது தெளிவு. மேலும் f-ன் வீச்சகம் (0,∞) ஆகும். இங்கு,    20 = 1 என இருப்பதால், அனைத்து x > 0-க்கும் 2x > 1 எனக் கிடைக்கிறது. மேலும், அனைத்து x < 0-க்கும் 2x < 1 எனக் கிடைக்கிறது. f : ℝ → (0, ∞) ஒரு மேற்கோர்த்தல் சார்பு எனக் கவனிக்க.

2. a = 1/2 எனக் கொள்க. g(x) = (1/2)x =1/2x, x∈ℝ என்க.

வரைபடத்திலிருந்து x அதிகரிக்கும் போது, g(x) =(1/2)x -ன் மதிப்பு குறைகிறது என்பது தெளிவு மற்றும் g(ℝ) = (0, ∞). மேலும், g(0) = 1 அனைத்து x <0-க்கு g (x) > 1 மற்றும் அனைத்து x > 0 -க்கு g(x) < 1 எனக் கிடைக்கும்.

குறிப்புரை : 

மேலே உள்ள எடுத்துக்காட்டுகளில் உள்ள கருத்துக்களின்படி, எந்தவொரு அடிமானம் 0 < a ≠ 1 கொண்ட படிக்குறிச் சார்புகள் f(x) = ax, ஒன்றுக்கொன்று மற்றும் மேற்கோர்த்தல் சார்பாக இருக்கும். அதன் சார்பகம் R மற்றும் துணை சார்பகம் (0, ∞) ஆகும்.

ஒரு சிறப்பு படிக்குறிச் சார்பு (A special exponential function)

அனைத்து படிக்குறிச் சார்புகளைவிட, f(x) = ex, x ∈ ℝ என்ற சார்பு முக்கியமானதாகக் கருதப்படுகிறது. ஏனெனில், இது கணிதவியல், அறிவியல் மற்றும் பொருளியல் ஆகியவற்றில் பயன்படுகின்றது. e என்பது என்ன? கீழே கொடுக்கப்பட்டுள்ள கூட்டு வட்டிக் கணக்கு, மாறிலி e-ன் மதிப்பைத் தருகிறது.

விளக்க எடுத்துக்காட்டு

கூட்டு வட்டி : P அசல், r = வட்டி வீதம் / 100, n என்பது ஒரு வருடத்தில் வட்டி கணக்கிடும் எண்ணிக்கை மற்றும் t என்பது வருடங்களின் எண்ணிக்கை . எனவே, A = P(1 + r/n)nt இது t வருடங்களில் கிடைக்கும் மொத்தத் தொகை காணும் சூத்திரம். n = 4 எனில், அது கால் வருடக் கூட்டு வட்டியாகும்.

(அதாவது, 3 மாதத்திற்கொருமுறை வட்டி கணக்கிட்டு அசலுடன் சேர்த்துக் கொள்ளப்படுகிறது). n = 12 எனில், அது மாதக் கூட்டு வட்டியாகும். n = 365 எனில் அது தினக் கூட்டு வட்டியாகும். n = 365 ஒரு மணி நேரம் மற்றும் ஒரு நிமிடம் கூட்டு வட்டி கணக்கிட இயலும். p மற்றும் மாறாமல் இருந்து கூட்டு வட்டி கணக்கிடும் எண்ணிக்கை அதிகரித்தால் கிடைக்கும் மொத்தத் தொகை அதிகரிக்கும் என்பதை நாம் அறிவோம். முதல் வகையாக P = 1,r=1 மற்றும் t = 1 கருதுவோம். An = (1+ 1/n)n என்க. எனவே, n அதிகமான எண்ணாக இருக்கும்போது எவ்வளவு பெரியது என்பதை நாம் உணரவேண்டும். எனவே, n = 10, 100, 10000, 100000, 100000000 என்ற வெவ்வேறு மதிப்புகளுக்கு A இன் மதிப்பை அட்டவணையில் காணலாம்.

n-ன் மதிப்பு அதிகரித்துக்கொண்டே போகும்போது 

An.-ன் மதிப்பு 2.718281815… -க்கு அருகில் அமைகிறது.

An இன் மதிப்பு e என்ற விகிதமுறா மெய்யெண்ணான 2.718281815-ஐ நெருங்குகிறது. எனவே, கூட்டு வட்டியின் சூத்திரம் A = Pert எனக் கொள்ளலாம்.

இங்கு வட்டி விகிதம் r, அசல் P மேலும், ஓர் ஆண்டிற்கு t முறை வட்டி கணக்கிடப்படுகிறது. இது தொடர் கூட்டு வட்டி எனப்படும்.

எடுத்துக்காட்டு 2.31 (i) சுருக்குக: (x1/2 y -3)1/2, x,y ≥ 0 (ii) சுருக்குக: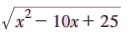

தீர்வு: 

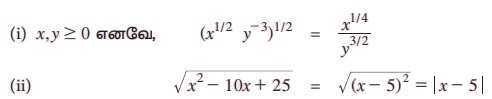
குறிப்பு: 

(i) (x1/4)4 = x ஆனால், (y4)1/4 = | y |

x ஒரு மிகை எண் எனில், x1/4 வரையறுக்கப்படுகிறது. ஆனால் y <0, எனினும் (y4)1/4 வரையறுக்கப்படுகிறது. ஒரு மிகை எண் மற்றும் அதன் 4 ஆம் அடுக்கு y4  எனவே, அது | y | என இருத்தல் வேண்டும். 

(ii) (x8 y4)1/4 = x2 | y | 

(iii) u,v, b ஆகியவை விகிதமுறு எண்கள் என்க. b ஒரு மிகை எண் என்க. அவை விகிதமுறு எண்களின் வர்க்கங்கள் அல்ல என்க. எனவே,u+v√b, u - v√b ஆகியவை ஒன்றுக்கொன்று இணை எண் (conjugates) எனப்படும். (u+ v√b)(u - v√b) = u2- bv2 என்பது ஒரு விகிதமுறு எண்ணாகும். ஒரு கோவையின் பகுதியில் u+v√b என்றிருப்பின் அதன் பகுதி மற்றும் தொகுதியை அதன் துணை எண் u - v√b ஆல் பெருக்கப் பகுதியில் விகிதமுறு எண் கிடைக்கும். 

(iv) (u√a-v√b) (u√a+v√b) = u2 a- v2 b-ஐப் பயன்ப டுத்தி, u√a+v√b பகுதியில் இருக்கும்பொழுது எளிய கோவை கிடைக்கும்.

எடுத்துக்காட்டு 2.32 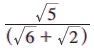 பகுதியை விகிதமுறு எண்ணாக்குக.

தீர்வு: 

எடுத்துக்காட்டு 2.33 7 - 4 √3-ன் வர்க்கமூலம் காண்க. 

தீர்வு:

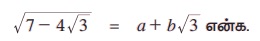
இங்கு, a, b ஆகியவை விகிதமுறு எண்கள். 

இருபுறமும் வர்க்கப்படுத்த,

7-4 √3 = a2 + 3b2 + 2ab √3 எனக் கிடைக்கும்.

எனவே,                 a2 + 3b2 = 7 மற்றும் 2ab = - 4

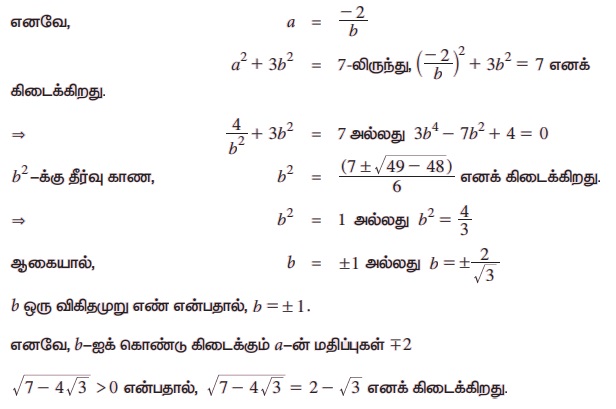
குறிப்பு: u,v ஆகிய விகிதமுறு எண்களைக் கொண்ட u+v √b-ன் வர்க்கமூலத்தை, x,y ஆகிய விகிதமுறு எண்களைக் கொண்ட x + y √b என்ற வடிவில் எப்பொழுதும் எழுத இயலாது. எடுத்துக்காட்டாக, 1 + √2 -ன் வர்க்க மூலம் a,b ஆகிய விகிதமுறு எண்களைக் கொண்ட a+b √2 என்ற அமைப்பில் எழுத முடியாது.

பயிற்சி 2.11

1. சுருக்குக.

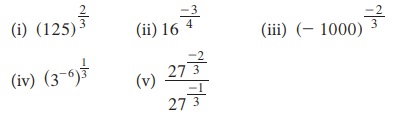
2. மதிப்பைக் காண்க: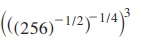

3. (x1/2 + x -1/2)2 = 9/2 எனில், x >1-க்கு (x1/2 – x-1/2)-ன் மதிப்பைக் காண்க 

4. சுருக்குக: 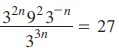அதன்மூலம் n-ன் மதிப்பைக் காண்க 

5. 32π/3 கன அளவு கொண்ட கோள வடிவுடைய நீர்த்தேக்கத் தொட்டியின் ஆரத்தைக் காண்க. 

6. விகிதமுறு எண்ணாக்குக.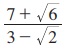

7. சுருக்குக.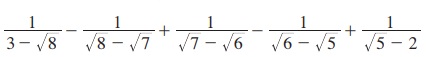

8. x = √2 + √3 எனில், x2+1/x2-2 --ன் மதிப்பைக் காண்க.