வரையறை, தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள், பயிற்சி | கணிதம் - நேரிய அசமன்பாடுகள் | 11th Mathematics : UNIT 2 : Basic Algebra
11வது கணக்கு : அலகு 2 : அடிப்படை இயற்கணிதம்
நேரிய அசமன்பாடுகள்
நேரிய அசமன்பாடுகள் (Linear Inequalities)
a,b ∈ R என்ற மாறிலிகளைக் கொண்ட f(x) = ax + b என்ற சார்பு நேரியல் சார்பு என்பதை நினைவு கூர்வோம். இதன் வரைபடம் ஒரு நேர்கோடு என்பதால் இதை நேரியல் சார்பு என்கிறோம். இங்கு, a என்பது கோட்டின் சாய்வு மற்றும் b என்பது y - வெட்டு துண்டு ஆகும். a ≠ 0, எனில், f(x) = ax + b = 0 என்பதைத் தீர்க்க x - வெட்டுத்துண்டு -b/a எனக் கிடைக்கும்.
சில நேரங்களில் நேரிய அசமன்பாடுகளை கருத்தில் கொள்ளும் தேவை உருவாகிறது. எடுத்துக்காட்டாக, "கோபுரத்தின் உயரம் 50 அடிக்கு மேல் இல்லை" என்ற கூற்றை விளக்க வேண்டும். x என்பது ‘அடி’யில் குறிக்கப்பட்ட கோபுரத்தின் உயரம் எனில் மேலே உள்ள கூற்றை எழுதும் முறை x ≤ 50 ஆகும்.
எடுத்துக்காட்டு 2.6 மாதாந்திர மின் பயன்பாட்டு கட்டணத்தின் ஒரு பகுதி மாறாது என்றும் மற்றொரு பகுதி பயன்படுத்திய மின்சாரத்தின் யூனிட் அளவைப் பொறுத்து மாறுவதாகவும் உள்ளது என்க. மின்வாரியம் அடிப்படைக் கட்டணமாக ₹110 என்றும் பயன்பாட்டுக் கட்டணம் ஒரு யூனிட்டுக்கு ₹4 என்றும் வசூலிக்கிறது. ஒருவர் தன் மின் கட்டணத்தை ₹250-க்குக் கீழ் இருக்கவேண்டும் என விருப்பப்பட்டால் அவரது மின் பயன்பாடு எவ்வளவாக இருக்க வேண்டும்.
தீர்வு:
x என்பதைப் பயன்படுத்திய மின்சாரத்தின் அளவு என்க. இங்கு x ≥ 0, இப்போது, மின்கட்டணம் ₹ 110 + 4x ஆகும். அது ₹250-க்குக் கீழ் இருக்கவேண்டும். எனவே, 110 + 4x < 250 என்ற அசமன்பாட்டின் அடிப்படையில் அமைய வேண்டும். அதாவது, 4x < 140 எனவே, 0 ≤ x < 35. ஒருவர் தன் கட்டணம் ₹250-க்கு கீழ் இருக்க, பயன்பாட்டு மின்சாரம் 35 யூனிட்டுக்குக் கீழ் இருக்கவேண்டும்.
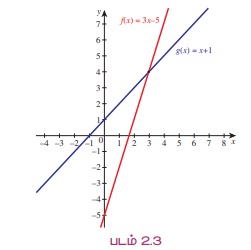
எடுத்துக்காட்டு 2.7 தீர்க்க: 3x – 5 ≤ x + 1
தீர்வு:
3 x - 5 ≤ x + 1 என்பது 2 x ≤ 6 ஆகும்.
எனவே, x < 3 அதாவது, தீர்வு (- ∞, 3] ஆகும்.
குறிப்பு: மேற்கண்ட எடுத்துக்காட்டினை வரைபடத்தின் மூலம் தீர்வு காணலாம். f(x) = 3 x - 5 மற்றும் g (x) = x + 1 (படம் 2.3) ஆகியவற்றை வரைய வேண்டும். பின்பு g-ன் வரைபடத்திற்கும் கீழ் உள்ள f-ன் வரைபடத்தின் மீதுள்ள x புள்ளிகளைக் காண வேண்டும்.
எடுத்துக்காட்டு 2.8 கீழ்க்கண்ட அசமன்பாட்டுத் தொகுப்பினைத் தீர்க்க: 3 x – 9 ≥ 0, 4 x - 10 ≤ 6
தீர்வு:
3 x – 9 ≥ 0 ⇒ 3 x ≥ 9 அதாவது, x ≥ 3 எனக் கிடைக்கும்.
அதேபோன்று, 4x – 10 ≤ 6 -லிருந்து, 4x ≤ 16 எனக் கிடைக்கும். அதாவது, x ≤ 4. தீர்வுகள் [3, ∞) மற்றும் (- ∞, 4)-ன் வெட்டுகணமாகும். எனவே, தீர்வு [3, 4].
எடுத்துக்காட்டு 2.9 A என்ற பெண் 446 பக்கங்களைக் கொண்ட ஒரு புத்தகத்தில் 271 பக்கங்களைப் படித்து முடித்துவிட்டாள். அவள் அப்புத்தகத்தை ஒரு வாரத்தில் படித்து முடிக்க வேண்டுமெனில், ஒரு நாளைக்குக் குறைந்தபட்சம் எத்தனை பக்கங்களை படிக்க வேண்டும்?
தீர்வு:
தினமும் படிக்கவேண்டிய பக்கங்களின் எண்ணிக்கையை x என்க. x நிறைவு செய்யும் அசமன்பாடு 7x + 271 ≥ 446. அதிலிருந்து, x ≥ 25 எனக் கிடைக்கிறது. எனவே அப்புத்தகத்தை ஒரு வாரத்தில் படித்து முடிக்கத் தினமும் குறைந்தது 25 பக்கங்கள் படிக்க வேண்டும்.
மேலே உள்ள எடுத்துக்காட்டுகளில் ஒவ்வொரு அசமன்பாடுகளும் ஒன்றுக்கும் மேற்பட்ட தீர்வுகளைத் தருகிறது. பொதுவாக அசமன்பாடுகளுக்கு தீர்வாக ஒரு வீச்சகம் கிடைக்கும்.
பயிற்சி 2.3
1. கீழ்க்கண்ட அசமன்பாடுகளை இடைவெளி அமைப்பில் எழுதுக.
(i) x ≥ - 1 மற்றும் x < 4
(ii) x ≤ 5 மற்றும் x ≥ -- 3
(iii) x < - 1 அல்லது x <3
(iv) - 2 x > 0 அல்லது 3 x - 4 < 11
2. 23 x < 100 -ன் தீர்வை
(i) x ∈ ℕ
(ii) x ∈ Z -க்கு காண்க.
3. - 2 x ≥ 9 -ன் தீர்வை
(i) x ∈ ℝ
(ii) x ∈ Z
(iii) x ∈ ℕ-க்கு காண்க.
4. தீர்வு காண்க
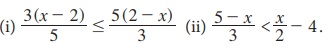
5. ஒவ்வொன்றும் 100 மதிப்பெண்கள் கொண்ட 5 பாடங்களில் மதிப்பெண்களின் சராசரி 90 அல்லது அதற்கும் மேல் இருந்தால் தரம் A ஆகும். ஒரு நபர் முதல் 4 பாடங்களில் பெற்ற மதிப்பெண்கள் 84, 87, 95, 91 எனில், ஐந்தாம் பாடத்தில் குறைந்தபட்சம் என்ன மதிப்பெண் பெற்றால் தரம் A கிடைக்கும்?
6. ஒரு உற்பத்தியாளர் 12 விழுக்காடு அமிலம் கொண்ட 600 லிட்டர் கரைசல் வைத்திருக்கிறார். இதனுடன் எத்தனை லிட்டர்கள் 30 விழுக்காடு அமிலத்தைக் கலந்தால் 15 விழுக்காட்டிற்கும் 18 விழுக்காட்டிற்கும் இடைப்பட்ட அடர்த்தி கொண்ட அமிலக் கரைசல் கிடைக்கும்?
7. 10ஐ விடப் பெரிய அடுத்தடுத்த இரண்டு ஒற்றைப்படை இயல் எண்களின் கூடுதல் 40ஐ விடக் குறைவாக இருக்க வேண்டுமெனில், அவ்வெண்களைக் காண்க.
8. ஒரு ஏவுகணை ஏவப்படுகிறது. t வினாடிகளுக்குப் பிறகு தரையில் இருந்து அதன் உயரம் h ஆனது h(t) = - 5t2 + 100t, 0 ≤ t ≤ 20 எனக் கொடுக்கப்பட்டுள்ளது. ஏவுகணை எந்நேரங்களில் 495 அடி உயரத்தை அடையும்.
9. தண்ணீர் குழாய் சரி செய்பவருக்குப் பின்வரும் முறைகளில் கூலி கொடுக்கப்படுகிறது. முதல் முறையில் ₹500-ம், ஒவ்வொரு மணி நேரத்திற்கும் ₹70 கணக்கிடப்பட்டுக் கொடுக்கப்படுகிறது. இரண்டாம் முறையில் ஒவ்வொரு மணி நேரத்திற்கு ₹120 எனக் கொடுக்கப்படுகிறது. ஒருவர் x மணி நேரம் வேலை செய்கிறார் எனில், x-ன் எம்மதிப்பிற்கு முதல் முறையில் அவருக்கு சிறந்த கூலி கிடைக்கும்?
10. A மற்றும் B ஆகியோர் ஒரே மாதிரியான வேலை செய்தாலும், அவர்களது மாத ஊதியம் ₹6000-க்கு மேல் வேறுபாடாக இருக்கிறது. B-ன் மாத ஊதியம் ₹27,000 எனில், A-ன் மாத ஊதியத்திற்கான சாத்தியக் கூறுகளைக் காண்க.