விகிதமுறுச் சார்புகள்

விகிதமுறுச் சார்புகள் (Rational Functions)

இரு பல்லுறுப்புக் கோவைகள் P(x) மற்றும் Q (x), Q(x) ≠ 0, ஆகியவற்றின் விகிதம் X-ஆல் ஆன விகிதமுறு கோவை எனப்படும்.

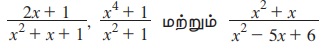ஆகியவை விகிதமுறு கோவைகளுக்குச் சில எடுத்துக்காட்டுகளாகும்.

பகுதி P(x)-ன் படி Q(x)-ன் படிக்குச் சமமாகவோ அல்லது அதைவிடப் பெரியதாகவே இருப்பின் P(x) = f(x) Q (x) + r(x) என எழுதலாம். இங்கு , r(x) = 0 அல்லது r (x)-ன் படி Q(x)-ன் படியைவிடக் குறைவாக இருக்கும். 

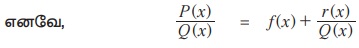
1. விகிதமுறு அசமன்பாடுகள் (Rational Inequalities)

எடுத்துக்காட்டு 2.24 தீர்க்க: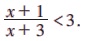

தீர்வு:

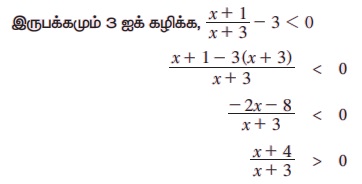
x + 4, x + 3, ஆகிய இரண்டுமே மிகையாகவோ அல்லது இரண்டுமே குறையாகவோ இருக்கும். எனவே, x + 3 மற்றும் x + 4 ஆகியவைகளின் குறியீடுகளைக் கீழ்க்கண்டவாறு காணலாம்.

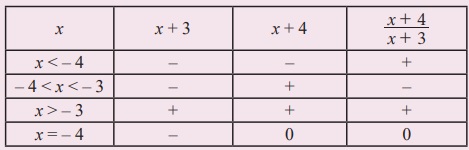
எனவே, தீர்வுக் கணம் (- ∞, - 4) U (- 3, ∞) ஆகும்.

குறிப்பு: எண் கோட்டின் இடைவெளிகளில் காரணிகளின் குறிகளைக் குறிப்பிட்டும் இவ்வகை விகிதமுறு அசமன்பாடுகளுக்குத் தீர்வு காணலாம்.

பயிற்சி 2.8

1. 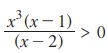எனில் x-ன் அனைத்து மதிப்புகளையும் காண்க. 

2. 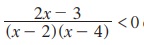என்ற அசமன்பாட்டை நிறைவு செய்யும் x-ன் அனைத்து மதிப்புகளையும் காண்க.

3. தீர்வு காண்க: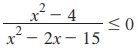

2. பகுதி பின்னங்கள் (Partial Fractions)

f(x) / g(x) என்ற விகிதமுறு கோவையில் f(x)-ன் படி g(x)-ன் படியை விட குறைவாக இருப்பின் அது ஒரு தகு பின்னமாகும். இங்கு மெய் பூஜ்ஜியங்கள் இல்லாமல் g(x)ஐ ஒருபடி மற்றும் இருபடி காரணிகளாக அமையும்படி காரணிப்படுத்த இயலும். எனவே, f(x)/g(x) ஐ எளிய உறுப்புகளைக் கொண்டு மாற்றி எழுதலாம். அதாவது உறுப்புகளின் கூடுதலாக பின்வருமாறு எழுதலாம்.-

(i) g(x) -ஐ x – a வகுக்கும் எனில்,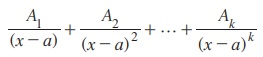

(ii) இங்கு x2 + ax + b-க்கு மெய் பூஜ்ஜியங்கள் இல்லாமலும் மற்றும் g(x) ஆனது (x + ax + b) ஆல் வகுபடுமாயின், 

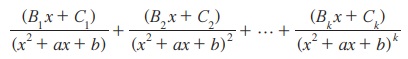 என எழுதலாம். இதனைப் பகுதி  பின்னங்களின் கூடுதலாக மாற்றப்பட்ட கோவை என்றழைக்கப்படுகிறது. 

குறிப்பு: கொடுக்கப்பட்ட விகிதமுறு சார்புக்கு அப்படி மாற்றப்பட்ட கோவை ஒருமைத்தன்மை வாய்ந்தது. இந்த முறை தொகை நுண்கணிதத்தில் தீர்வு வெகுவாகப் பயன்படுகிறது. சில எடுத்துக்காட்டுகளை இப்பொழுது நாம் விவாதிக்கலாம்.

எடுத்துக்காட்டு 2.25 பகுதி பின்னங்களாகப் பிரிக்கவும்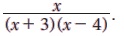

தீர்வு:

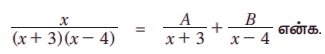
இங்கு A மற்றும் B மாறிலிகள்

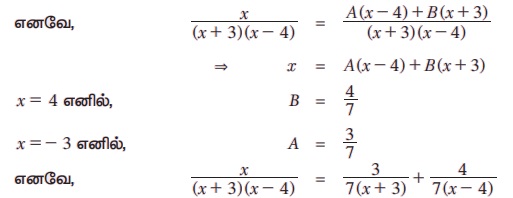
குறிப்பு: பகுதியின் பூஜ்ஜியங்கள் வெவ்வேறாகவும், ℝ-ல் உள்ளதாகவோ அமையும் போது மேற்கண்ட வழிமுறை பயன்படுத்தப்படுகிறது.

எடுத்துக்காட்டு 2.26 பகுதி பின்னங்களாகப் பிரிக்கவும்: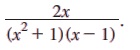

தீர்வு: 

இதில், பகுதியில் உள்ள ஒரு காரணி (x2 + 1)-க்கு மெய்யெண் பூஜ்ஜியம் இல்லை .

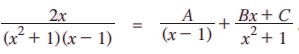  இங்கு, A, B, C மாறிலிகள். 

 2x = A (x2 + 1) + (Bx + C) (x - 1) எனக் கிடைக்கும். 

x = 1 எனும்போது A = 1, 

x = 0 எனும்போது A - C = 0 எனவே, A = C = 1 

x=- 1 எனும்போது 2A – 2(C - B) = - 2 ⇒ B = -1

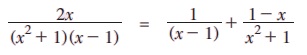
பகுதியில் ஒன்றுக்கு மேற்பட்ட பெருக்கல்படி கொண்ட மெய் பூஜ்ஜியங்கள் உள்ள நிலைமையை நாம் இப்பொழுது காண்போம்.

எடுத்துக்காட்டு 2.27 பகுதி பின்னங்களாகப் பிரிக்கவும்: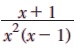

தீர்வு:

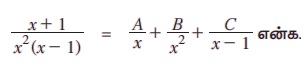
எனவே,    x + 1 = Ax (x - 1) + B(x - 1) + Cx2

x = 0 எனும்போது B = -1, x = 1 எனும்போது C = 2

x = - 1 எனும்போது 2A - 2B + C = 0 ⇒ A = - 2

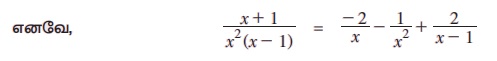
பயிற்சி 2.9

கீழ்க்காணும் விகிதமுறு கோவைகளைப் பகுதி பின்னங்களாகப் பிரித்தெழுதுக.

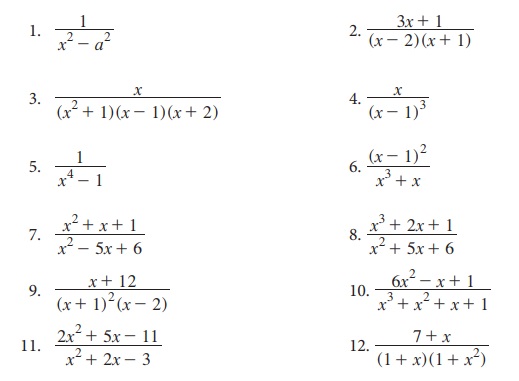
3. ஒரு படி அசமன்பாடுகளின் வரைபடங்கள் (Graphical Representation of Linear Inequalities)

ax + by = c என்ற ஒரு நேர்க்கோடு கார்டீசியன் தளத்தை இரண்டாகப் பிரிக்கிறது. ஒவ்வொரு பகுதியும் ஒரு அரைத்தளமாகும். x = c என்ற நிலைக்குத்துக்கோடு, இடது மற்றும் வலது அரைத்தளங்களாகவும், y = k என்ற கிடைமட்டக் கோடு, மேல் மற்றும் கீழ் அரைத்தளங்களாகவும் பிரிக்கிறது.

ax + by = c இன் மீது அமையாத ஒரு புள்ளி, அக்கோடு பிரிக்கும் அரைத்தளங்களில் ஏதேனும் ஒன்றில் மட்டும் அமைந்து ax + by <c மற்றும் ax + by >c ஆகிய அசமன்பாடுகளில் ஒன்றை மட்டும் நிறைவு செய்கிறது.

ax + by < c என்ற அசமன்பாடு குறிக்கும் அரைத்தளத்தைக் காண ஏதேனும் ஒரு புள்ளி P-ஐ அதில் பிரதியிட வேண்டும். அசமன்பாடு நிறைவுபெற்றால் P என்ற புள்ளி அந்த அரைத்தளத்தில் அமைந்துள்ளது எனலாம். நிறைவு செய்யவில்லை எனில், அப்புள்ளி தரப்பட்ட அசமன்பாடு குறிக்காத மற்றொரு தளத்தில் அமைந்துள்ளது எனலாம். c ≠ 0 எனில் p-ஐ ஆதிப்புள்ளியாக எடுத்துக் கொள்வது மிக எளிது.

எடுத்துக்காட்டு 2.28  x ≥ 2 என்ற அசமன்பாடு குறிக்கும் பகுதியை நிழலிட்டுக் காட்டுக. 

தீர்வு:

x = 2 என்ற சமன்பாட்டினைக் கருத்தில் கொள்க. இது y அச்சிலிருந்து 2 அலகுகள் தூரத்திலுள்ள y அச்சிற்கு இணையான கோடு ஆகும். இக்கோடு கார்டீசியன் தளத்தை இரண்டு பாகங்களாகப் பிரிக்கின்றது. (0, 0) -ஐ அசமன்பாட்டில் பிரதியிட 0 ≥ 2 எனக் கிடைக்கிறது. இது உண்மையல்ல. எனவே, ஆதிப்புள்ளியை தன்னகத்தே கொள்ளாத பாகம் x ≥ 2 என்ற அசமன்பாட்டினைக் குறிக்கும். படத்தில் நிழலிட்ட பகுதியே அசமன்பாட்டின் தீர்வாகும். x ≥ 2 என்பதால் x = 2 என்ற கோட்டின் மீதுள்ள புள்ளிகளும் அதன் தீர்வாகும்.

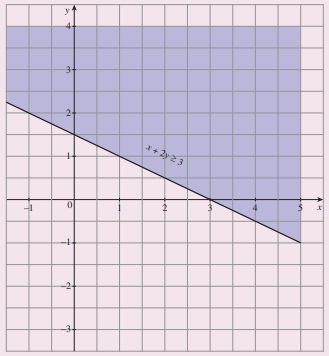
எடுத்துக்காட்டு 2.29 x + 2y > 3 என்ற அசமன்பாடு குறிக்கும் பகுதியை நிழலிட்டுக் காட்டுக.

நிரூபணம்

x + 2y = 3 என்ற கோடு கார்டீசியன் தளத்தை இரண்டு பகுதிகளாகப் பிரிக்கிறது.

x + 2y > 3 குறிக்கும் பகுதியைக் காண ஒரு பகுதியில் உள்ள ஏதேனும் ஒரு புள்ளியைப்பிரதியிட வேண்டும். அசமன்பாட்டில் (0, 0)-ஐ பிரதியிடக் கிடைப்பது 0 > 3 ஆகும். இது உண்மையல்ல. எனவே ஆதியைத் தன்னகத்தே பெற்றிராத நிழலிட்ட பகுதியே கொடுக்கப்பட்ட அசமன்பாட்டைக் குறிக்கும் பகுதியாகும்.

எடுத்துக்காட்டு 2.30  x + y ≥ 3, 2x – y ≤ 5 மற்றும் - x + 2y ≤ 3 ஆகிய அசமன்பாடுகளின் தொகுப்பிற்கு வரைபடப் பகுதியாகத் தீர்வு காண்க.

தீர்வு :

கோட்டின் மீதுள்ள இரு புள்ளிகள் தெரியுமானால் அக்கோட்டை வரைய இயலும்.

x + y = 3-ன் மீது (3, 0) மற்றும் (0, 3) ஆகிய புள்ளிகள் அமையும் என்பதை எளிதில் கண்டறியலாம்.

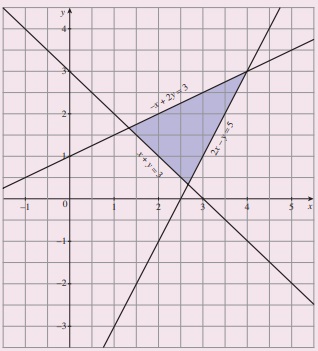
x + y = 3, 2x – y = 5 மற்றும் – x + 2y = 3 ஆகிய மூன்று கோடுகளையும் வரைக.

இப்போது, (0, 0) புள்ளி x + y ≥ 3-ஐ நிறைவு செய்யாது. (0, 0)ஐ தன்னகத்தே பெற்றிருக்காத x + y = 3 பகுதியே x + y ≥ 3 இன் தீர்வுகணமாகும்.

இதேபோன்று, 2x – y ≤ 5 ஐ ஆதிப்புள்ளி நிறைவு செய்து ஆதியைக் கொண்ட பகுதியே 2x – y ≤ 5 இன் தீர்வுக் கணமாகும்.

மேலும், - x + 2y  ≤ 3 ஐ ஆதிப்புள்ளி நிறைவு செய்வதால் ஆதியைக் கொண்ட பகுதியே - x + 2y ≤ 3 இன் தீர்வுக் கணமாகும்.

மூன்று பகுதிகளுக்கும் பொதுவான பகுதியே கொடுக்கப்பட்ட ஒருபடி அசமன்பாடுகளின் தொகுப்பிற்குத் தீர்வுக் கணமாகும்.

பயிற்சி 2.10

கீழே கொடுக்கப்பட்ட அசமன்பாடுகள் குறிக்கும் பகுதியைக் காண்க.

1. x ≤ 3y,       x ≥ y. 

2. y ≥ 2x,      - 2x + 3y ≤ 6. 

3. 3x + 5y ≥ 45, x ≥ 0, y ≥ 0.

4. 2x + 3y ≤ 35, y ≥ 2, x ≥ 5

5. 2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0. 

6. x- 2y ≥ 0, 2x – y ≤ - 2, x ≥ 0, y ≥ 0. 

7. 2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6.