மெய்யெண்களின் அமைப்பு

மெய்யெண்களின் அமைப்பு (Real Number System)

முதலில் எவ்வாறு மெய்யெண்களின் அமைப்பு உருவானது என்பதனை மீள் பார்வையிடுவோம். இயல் எண்கள் ℕ-லிருந்து தொடங்குவோம்.

1. விகிதமுறு எண்கள் (Rational Numbers)

ℕ = {1, 2, 3,...} என்பது பொருட்களை எண்ணிடப் போதுமான கணமாகும். இலாப-நஷ்டங்களைக் கையாள வசதியாக ℕ -ஐ விரிவு செய்து அனைத்து முழு எண்களின் கணமாக ℤ = {..., - 4, - 3, - 2, - 1, 0,1,2, … } விரிவாக்கப்பட்டது. இக்கணம் இயல் எண்கள் (மிகை முழு எண்கள்), பூஜ்ஜியம் மற்றும் குறை குறியீடுகளுடன் கூடிய இயல் எண்கள் (குறை முழு எண்கள்) ஆகியவற்றைக் கொண்டுள்ளது. {0, 1, 2, 3,...} என்பதைக் குறையற்ற முழு எண்களின் கணம் என்போம். மேலும், இதனை W ஆல் குறிப்போம். இக்கணம் இயலெண்களின் கணத்திலிருந்து பூஜ்ஜியம் என்ற ஒரே ஒரு உறுப்பால் மட்டுமே வேறுபடுகிறது.

இப்போது ஒரு அப்பத்தினை ஐந்து சமபங்காகப் பிரிக்க வேண்டும் என்பது 5x = 1 என்ற சமன்பாட்டின் தீர்வு காண்பதற்கு ஒப்பாகும். ℤ-ல் மட்டும் இதன் தீர்வுகளைக் காண இயலாது. எனவே, ℤஐ விரிவுபடுத்தி 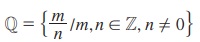என பின்னங்களால் உருவாக்கப்பட்டது. ஆகவே, ℚ-ல் உள்ள ஒவ்வொரு எண்ணும் விகிதமுறு எண் (rational number) என அழைக்கப்படுகிறது. 

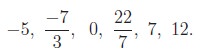ஆகியவை விகிதமுறு எண்களுக்கான சில எடுத்துக்காட்டுகள் ஆகும். 

விகிதமுறு எண்கள், முடியக் கூடிய தசமங்கள் அல்லது முடிவுறாச் சீர் சூழல் தசமங்களைக் கொண்ட எண்களின் கணம் என்பதை முந்தைய வகுப்புகளில் கண்டோம். 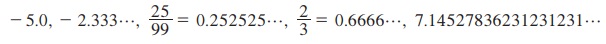ஆகியவை விகிதமுறு எண்களுக்கான சில எடுத்துக்காட்டுகள் ஆகும்.

2. எண் கோடு (The Number Line)

எண்கோடு என்பதை நினைவு கொள்வோம். இது 0-ஐ மையமாகவும், அதன் வலப்பக்கம் 1 அமைந்துள்ள கிடைமட்டக்கோடு ஆகும். 0-விற்கும் 1-க்கும் இடைப்பட்ட தூரம் ஒரு அலகு என வரையறுக்கலாம். இப்போது 1-க்கு வலப்பக்கம் ஒரு அலகு தூரத்தில் 2 ஐக் குறிக்கவும். இதேபோன்று, x என்ற மிகை விகிதமுறு எண்ணை 0-விலிருந்து x அலகு வலப்புறத்தில் அக்கோட்டில் குறிக்கலாம். இதேபோன்று குறை விகிதமுறு எண் -r, r > 0-ஐ 0-விற்கு இடப்பக்கம் r அலகு தூரத்தில் குறிக்கலாம். மேலும், x,y ∈ ℚ, x < y எனில் y இன் இடப்புறத்தில் x இருக்கும். மேலும், x < (x + y)/2  < y. எனவே, இரு வெவ்வேறு விகிதமுறு எண்களுக்கு இடையில் மற்றொரு விகிதமுறு எண் இருக்கும்.

கேள்வி:

விகிதமுறு எண்களை முழுக்கோட்டிலும் குறித்து விடமுடியுமா?    

இதற்குப் பதில் 'முடியாது' என்பதைக் கீழ்க்கண்டவாறு விளக்கலாம். 1 அலகு பக்கங்களைக் கொண்ட சதுரத்தைக் கொள்க. பிதாகரஸ் தேற்றத்தின்படி அதன் மூலைவிட்டத்தின் நீளம் √2 அலகு ஆகும்.

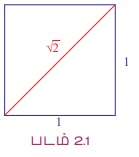
3. விகிதமுறா எண்கள் (Irrational Numbers)

தேற்றம் 2.1 √2 ஒரு விகிதமுறு எண் அல்ல. 

நிரூபணம்: √2 விகிதமுறு எண் என எடுத்துக்கொண்டால் √2 = m/n, இதில் m, n, ஆகியவை 1-ஐ விட வேறு பெரிய பொதுக் காரணியில்லாத இயலெண்கள் என எழுத இயலும். இப்போது, m2 = 2n2 என்பதால் m2 என்பது ஒரு இரட்டைப்படை எண் ஆகிறது. எனவே, m ஒரு இரட்டைப்படை எண் m = 2k என்க. மேலும், 2n2 = 4k2 என்பதால் n2 = 2k2 ஆகும். எனவே, n ஒரு இரட்டைப்படை எண். இவ்வாறு m மற்றும் n ஆகியவை பொதுக்காரணி 2 உடைய இரட்டைப்படை எண்களாக மாறுகிறது. இது முரணான முடிவு ஆகும். எனவே √2 என்பது ஒரு விகிதமுறா எண் (irrational number) ஆகும்.

குறிப்புரை :

(i) மேலே உள்ள நிரூபணத்தில் நாம் எதை நிறுவ வேண்டுமோ அதற்கு நேரெதிரான கூற்றை எடுத்துக்கொண்டு முரணான கூற்றினை வருவித்தோம் என்பதைக் கவனிக்கவும். இம்முறை “முரண்பாட்டு கூற்று மூலம்” நிரூபித்தல் ஆகும். 

(ii) எண் கோட்டில் விகிதமுறு எண்களால் குறிக்கப்படும் புள்ளிகளைத் தவிர வேறு புள்ளிகளும் உண்டு. 

(i) எண் கோட்டில் விகிதமுறு எண்களால் குறிக்கப்படாத புள்ளிகளைக் குறிக்கும் எண்களை விகிதமுறா எண்கள் ℚ' என்போம். (படம் 1.2 இல் எண்கோட்டைப் பார்க்க) 

ஒவ்வொரு மெய்யெண்ணும், விகிதமுறு அல்லது விகிதமுறா எண்ணாக இருக்கவேண்டும். ஆனால் இரண்டுமாக இருக்க முடியாது. எனவே, R = Q ∪ Q’ மற்றும் Q ∩ Q’ = ∅.

முடிவுறும் தசமங்களைக் கொண்ட எண்களும் முடிவுறாச் சீர் சூழல் தசமங்களைக் கொண்ட எண்களும் விகிதமுறு எண்கள் என்பதை அறிவோம். தசம முறையில் எழுதப்படும் விகிதமுறா எண்கள் முடிவுறாச் சீர் சூழல் தன்மையற்ற தசமங்களைப் பெற்றிருக்கும். ℝ என்ற மெய்யெண்களின் கணத்திலுள்ளவைகளை எண் கோட்டிலுள்ள புள்ளிகளாகக் கொள்ளலாம். மேலும், x < y  எனில், y-க்கு இடப்பக்கத்தில் x அமையும்.

ஒரு எண்கோட்டில் 2 மற்றும் 3-ன் வர்க்க மூலங்களைக் குறிப்பதை படம் 2.2-ல் காணலாம்.

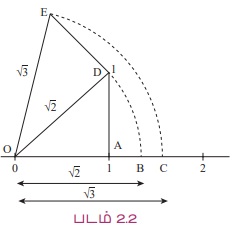
ℕ ⊂ W ⊂ ℤ ⊂ ℚ ⊂ ℝ என்பதை அறிவோம்.

விகிதமுறா எண்களை நடைமுறை வாழ்வில் சில இடங்களில் காணலாம். 2000 ஆண்டுகளுக்கு முன்பு எகிப்தியர்கள், வட்டங்களின் சுற்றளவும் அதன் விட்டமும் சம விகிதத்தில் அமைவதைக் கண்டார்கள். இந்த மாறிலி π-ஐ ஜோகன் ஹென்ரிச் லாம்பர்ட் (Johann Heinrich Lambert), 1767-ல் ஒரு விகிதமுறா எண் என நிரூபித்தார். 9 தசமத் திருத்தமாக π-ன் மதிப்பு 3.141592654 ஆகும். வட்டத்தின் பரப்பு மற்றும் கோளத்தின் கன அளவு ஆகியவற்றைக் கணக்கிடும்போது பயன்படுத்தப்படும் 22/7 மற்றும் 3.14 ஆகியவை π-ன் தோராய மதிப்புகளாகும்.

குறிப்பு: ஒரு வட்டத்தின் சுற்றளவிற்கும் அதன் விட்டத்திற்கும் உள்ள விகிதம் π என்ற விகிதமுறா எண் ஆகும்.

கணிதத்தின் அடிப்படையான மெய்யெண்களின் அமைப்பின் பண்புகளை நினைவு கூர்வோம்.

4. மெய்யெண்களின் பண்புகள் (Properties of Real Numbers)

(i) a,b ∈ ℝ எனில் a + b ∈ ℝ மற்றும் ab ∈ ℝ (இரண்டு மெய்யெண்களின் கூடுதல் ஒரு மெய்யெண் மற்றும் இரு மெய்யெண்களின் பெருக்கல் ஒரு மெய்யெண் ஆகும்). 

(ii) a,b,c ∈ ℝ எனில் (a + b) + c = a + (b + c) மற்றும் a(bc) = (ab)c (மூன்று மெய்யெண்களை கூட்டும்போது (பெருக்கும்போது) எந்த இரண்டு எண்களையும் முதலில் கூட்டலாம் (பெருக்கலாம்))

(iii) a ∈ ℝ எனில், a + 0 = a மற்றும் a(1) = a.

(iv) a ∈ ℝ எனில், a + (- a) = 0 மற்றும் b ∈ ℝ - {0}, b(1/b)= 1

(v) a,b ∈ ℝ எனில், a + b = b + a மற்றும் ab = ba.

(vi) a, b, c ∈ ℝ எனில், a(b + c) = ab + ac.

(vii) a, b ∈ ℝ, a < b ↔ b – a > 0. 

(viii) a ∈ ℝ எனில், a2 ≥ 0. 

(ix) a,b ∈ ℝ எனில், கீழ்க்காண்பனவற்றில் ஒன்று மட்டுமே உண்மை. அதாவது a = b அல்லது a < b அல்லது a > b.

(x) a, b ∈ ℝ மற்றும் a < b எனில், a + c < b + c இங்கு, c ∈ ℝ.

(xi) a, b ∈ ℝ மற்றும் a < b எனில், ax < bx இங்கு, x > 0.

(xii) a, b ∈ ℝ மற்றும் a < b எனில், ay > by இங்கு, y < 0.

பயிற்சி 2.1

1. 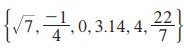ஆகிய ஒவ்வொரு எண்ணினையும் ℕ, ℚ, ℝ - ℚ அல்லது ℤ என்ற அடிப்படையில் எழுதுக.

2. √3 ஒரு விகிதமுறா எண் எனக்காட்டுக. (குறிப்பு: √2 ∉ ℚ-க்குப் பயன்படுத்திய முறையை பின்பற்றவும்) 

3. தனித்த (அ) நன்கு வரையறுக்கப்பட்ட இரண்டு விகிதமுறா எண்கள் உள்ளனவா எனில், அவ்விரு விகிதமுறா எண்களின் வித்தியாசம் ஒரு விகிதமுறு எண்ணாக இருக்க முடியுமா? நியாயப்படுத்துக. 

4. இரு விகிதமுறா எண்களின் கூடுதல் விகிதமுறு எண்ணாக அமையுமாறு விகிதமுறா எண்களைக் காண்க. இரு விகிதமுறா எண்களின் பெருக்கல் விகிதமுறு எண்ணாக அமையுமாறு இரண்டு விகிதமுறா எண்களைக் காணமுடியுமா? 

5. 1/21000-ஐவிட சிறிய மிகை எண் காண்க. நியாயப்படுத்துக.