மடக்கை

மடக்கை (Logarithm)

அடிமானம் 0 < a ≠ 1-க்கு, சார்பகம் ℝ மற்றும் வீச்சகம் (0, ∞) உடைய படிக்குறிச் சார்பு f(x) = ax என வரையறுக்கப்படுகிறது என்பதை அறிவோம். f(x) ஒரு இருபுறச் சார்பு (bijection) என்பதால் இதற்கு நேர்மாறு உண்டு. இதன் நேர்மாறு சார்பு மடக்கைச் சார்பு (logarithmic function) எனப்படும். அது log (.) எனக் குறிக்கப்படுகிறது. f(x) என்பது x-லிருந்து y = ax வரை எனில், loga (.) என்பது y இலிருந்து x-க்கான சார்பாகும். 

அதாவது, 0 < a ≠ 1 எனவே, y = ax மற்றும் logay = x ஆகியவை சமானமானவையாகும்.

எடுத்துக்காட்டாக, 34 = 81 ஐ log3(81) = 4 என எழுதலாம். a மற்றும் y கொடுக்கப்பட்டிருப்பின் ax = y-ஐ நிறைவு செய்யும். a-ன் எந்த அடுக்கு x-க்கு y மதிப்பு கிடைக்கும் என்பதை மடக்கைக் கண்டறிகிறது. "ஒரு குறிப்பிட்ட முதலீடு ஒரு எதிர்பார்த்த தொகையாகப் பெருகுவதற்கு எவ்வளவு ஆண்டுகள் ஆகும்?" என்பது போன்ற நடைமுறையில் உள்ள கணக்குகளைத் தீர்வு காணப் பயன்படுகிறது. மிகச் சிறிய மற்றும் மிகப் பெரிய எண்களைப் பெருக்குவதற்கும் மடக்கைப் பயன்படுகிறது.

குறிப்பு: (i) அனைத்து x ∈ ℝ மற்றும் ax > 0-க்கும் படிக்குறிச் சார்பு ax வரையறை செய்யப்பட்டுள்ளதால், log (.) என்பது மிகை மெய்யெண்களுக்கு மட்டுமே வரையறுக்கப்படும். 

(ii) மேலும், எந்தவொரு அடிமானம் a-க்கும் a0 = 1 என்பதால் loga (1) = 0 ஆகும்.

1. மடக்கையின் பண்புகள் (Properties of Logarithm)

(i) x ∈ (0, ∞)-க்கு alogax = x மற்றும் loga (ay) = y. இங்கு y ∈ ℝ. 

(ii) x,y > 0 எனில், loga (xy) = loga x+ loga y (பெருக்கல் விதி) 

(iii) x,y > 0 எனில், loga(x/y) = logax - logay (வகுத்தல் விதி) 

(iv) x > 0, r ∈ ℝ எனில், logaxr = rlogax (அடுக்கு விதி)

 (v) x > 0 மற்றும் a, b, அடிமானங்கள் எனில், logbx = logax/logab (அடிமான மாற்று விதி)

நிரூபணம் :

அடிமானம் a உடைய படிக்குறிச் சார்பு மற்றும் மடக்கைச் சார்புகள் ஒன்றுக்கொன்று நேர்மாறு என்பதால்,

(i) வரையறையின்படி உண்மை 

(ii) x,y > 0-க்கு logax = u, logay = v மற்றும் loga (xy) = w என்க. 

படிக்குறிச் சார்புகளாக எழுத, au = x, ay= y மற்றும் aw = xy

aw = xy = auav = au-v எனவே, w = u+ v 

எனவே, loga (xy) = logax + logay.

(iii) loga x = u, logay = v, மற்றும் loga x/y = w. 

எனவே au = x, av = y மற்றும் aw = x/y

எனவே,  aw = x/y = au/av = au-v = w = u - v

இவ்வாறாக , loga(x/y) = loga x - logay

(iv) loga x = u என்க

எனவே, au = x, xr = (au)r = aru

ஆகையால், loga xr = ru = rloga x

(v) logb x = V என்க. bv = x ஆகும்.

இருபுறமும் அடிமானம் a உடைய மடக்கைக் எடுக்க, loga bv = loga x 

அடுக்கு விதியின்படி,          logabv = v loga b 

எனவே, vloga b = loga x

எனவே,  logbx =  logax/logab, b>0

குறிப்புரை : 

(i) a = 10-ன் மடக்கைச் சார்பு log10x ஆகும். இது பொது மடக்கை (common logarithm) எனப்படும்.

(ii) a = e (ஒரு விகிதமுறா எண், தோராயமாக அதன் மதிப்பு 2.718) எனில், log x என்பது இயற்கை மடக்கை (natural logarithm) எனப்படும். இது In x எனக் குறிக்கப்படுகிறது. மேலே குறிப்பிட்ட மடக்கைச் சார்புகள் அறிவியலிலும் பொறியியலிலும் அதிகம் பயன்படுகிறது. இயற்கை மடக்கை இயல்பாக இடம் பெறுகிறது. Loge x-ஐ logx எனவும் எழுதலாம்.

(iii) a = 2 எனில், மடக்கைச் சார்பு log2x இரண்டடிமான மடக்கைச் சார்பு எனப்படும். இது கணிப்பொறி அறிவியலில் இடம் பெறுகிறது.

 (iv) loga35= loga (7* 5) = loga 7 + loga 5

loga50/3 = loga 50 – loga 3

loga22x = xloga 22

log550 = log1050/ log10 5

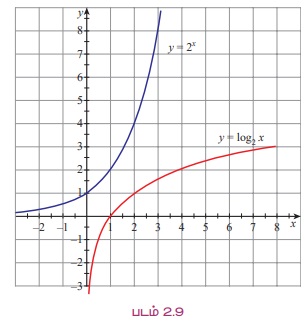
(v) மடக்கைச் சார்பு மற்றும் அடுக்குச் சார்புகளின் வரைபடம் கீழே கொடுக்கப்பட்டுள்ளது.

எடுத்துக்காட்டு 2.34 1728-க்கு அடிமானம் 2√3 உடைய மடக்கையைக் காண்க.

தீர்வு: 

Log2√3 1728 = x என்க.

பின்பு,    (2 √3)x = 1728 = 26 33 = 26 (√3)6 

எனவே,   (2√3)x = (2√3)6 ⇒ x = 6 எனவே, log2√3 1728 = 6

எடுத்துக்காட்டு 2.35 324-க்கு அடிமானம் a உடைய மடக்கை மதிப்பு 4 எனில் a-ன் மதிப்பைக் காண்க.

தீர்வு:

loga 324 = 4 எனக் கொடுக்கப்பட்டுள்ளது.

a4 = 324 = 34(√2)4

எனவே,    a = 3 √2

எடுத்துக்காட்டு 2.36 log 75/16 – 2log5/9 + log32/243 = log 2 என நிறுவுக. 

தீர்வு:

மடக்கையின் பண்புகளைப் பயன்படுத்தி,

log 75/16 - 2log5/9 + log 32/243 = log75 - log16 – 2 log 5 + 2 log 9 + log 32 - log 243

(வகுத்தல் விதியின்படி)

= log 3 + log 25 – log 16 - log 25 + log 81 + log 16 + log 2 - log 81 – log 3 

= log 2

எடுத்துக்காட்டு 2.37 log2x + log4 x + log16x = 7/2 எனில், x -ன் மதிப்பைக் காண்க.

தீர்வு:

x > 0 என்பதைக் கவனத்தில் கொள்க.

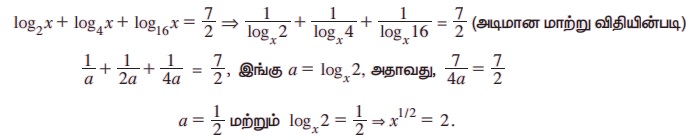
எனவே,  x = 22 = 4

எடுத்துக்காட்டு 2.38 தீர்வு காண்க: xlog3x = 9

தீர்வு:

                 log3 x = y என்க.

                           x = 3y மற்றும் 3y2 = 9 

எனவே,         y2 = 2, y = √2, -√2

                       x = 3√2, 3-√2

எடுத்துக்காட்டு 2.39 log35 log2527 -ன் மதிப்பைக் காண்க.

தீர்வு:

 log35 log2527 = log35 log2533

 = log35 × 3 log253 (அடுக்கு விதியின்படி)

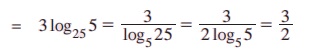
எடுத்துக்காட்டு 2.40 log102 = 0.30103, log103 = 0.47712 (தோராய மதிப்புகள்) எனில், 28 312-ல் எத்தனை இலக்கங்கள் உண்டு என்பதைக் காண்க. 

தீர்வு:

N = 28 312-க்கு n  + 1 இலக்கங்கள் உண்டு என்க.

1 ≤ b < 10 என்றிருக்குமாறு N -ஐ 10n × b என்ற அமைப்பில் எழுதலாம். 

10 அடிமான மடக்கையை இருபுறமும் எடுக்க,

log N = log(10n b) = n log 10 + log b = n + log b என நமக்குக் கிடைக்கிறது. 

log N = log 28 312 = 8 log 2 + 12 log 3 = 8 × 0.30103 + 12 × 0.47712 = 8.13368

இவ்வாறாக, n + log b = 8.13368 எனக் கிடைக்கிறது.

1 ≤ b < 10 என்பதால் இலக்கங்களின் எண்ணிக்கை 9.

பயிற்சி 2.12

1. b > 0 மற்றும் b ≠ 1 எனில், y = bx-ஐ மடக்கை அமைப்பில் எழுதுக. மேலும், இந்த மடக்கைச் சார்பின் சார்பகம் மற்றும் வீச்சகம் ஆகியவற்றை எழுதுக.

2. மதிப்பு காண்க: log927 – log279

3. log8x + log4x + log2x = 11-ன் தீர்வு காண்க. 

4. log4 28x = 2log28 -ன் தீர்வு காண்க. 

5. a2 + b2 = 7ab எனில், log a+b/3 = 1/2 (log a + log b) எனக் காண்க 

6. log a2/bc + log b2/ca + log c2/ab = 0 என நிறுவுக. 

7. log2 + 16 log 16/15 + 12 log 25/24 + 7 log 81/80 = 1 என நிறுவுக. 

8. 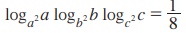என நிறுவுக.

9. 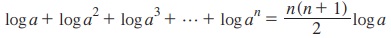என நிறுவுக.

10. 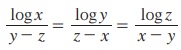எனில், xyz = 1 எனக் காண்க. 

11. log2x - 3log12 x = 6-ன் தீர்வு காண்க.

12. log5-x (x2 - 6x + 65) = 2-ன் தீர்வு காண்க.