மீ.பெ.கா மற்றும் மீ.சி.ம – வின் பயன்பாட்டுக் கணக்குகள்

மீ.பெ.கா மற்றும் மீ.சி.ம – வின் பயன்பாட்டுக் கணக்குகள்

அன்றாட வாழ்க்கைச் சூழல்களில் மீ.பெ.கா மற்றும் மீ.சி.ம கருத்துகள் இடம்பெறும் வாக்கியக் கணக்குகளைக் கீழே காணலாம்.

எடுத்துக்காட்டு 6:

62, 78 மற்றும் 109–ஐ வகுத்து முறையே 2, 3 மற்றும் 4–ஐ மீதிகளாகக் கொடுக்கும் மீப்பெரு பொதுக் காரணி என்ன?

தீர்வு:

கொடுக்கப்பட்ட எண்களில் மீதியைக் கழிக்க. 62 – 2, 78 – 3 மற்றும் 109 – 4, அதாவது 60, 75 மற்றும் 105–ஐ வகுக்கும் பொதுக் காரணிகளைக் காணவும். 60, 75 மற்றும் 105–ஐ வகுக்கும் மிகப்பெரிய எண்ணானது அவற்றின் மீ.பெ.கா. ஆகும்.

60 = 2 × 2 × 3× 5

75 = 3 × 5 × 5

105 = 3 × 5 × 7

ஆகவே, மீ.பெ.கா = 3 × 5 = 15 ஆனது 62, 78, 109–ஐ வகுத்து முறையே 2, 3 ,4–ஐ மீதியாகக் கொடுக்கும் மிகப் பெரிய எண் ஆகும்.

எடுத்துக்காட்டு 7: நூல் விற்பனையாளர் 175 ஆங்கில நூல்களையும் 245 அறிவியல் நூல்களையும் 385 கணித நூல்களையும் வைத்துள்ளார். ஒவ்வொரு பெட்டியிலும் பாட வாரியாகச் சம எண்ணிக்கையில் மூன்று பாட நூல்களையும் வைத்து விற்க விரும்புகிறார். அதிகபட்சமாக எத்தனைப் பெட்டிகள் தேவைப்படும்? ஒரு பெட்டியில் உள்ள ஒவ்வொரு பாட நூல்களின் எண்ணிக்கையைக் காண்க.

தீர்வு :

மீ.பெ.கா–வை பயன்படுத்தி இந்தக் கணக்கைத் தீர்க்கலாம்.

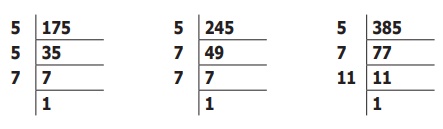
எனவே, 175, 245 மற்றும் 385 இன் மீ.பெ.கா. காண வேண்டும்.

 175 = 5 × 5 × 7; 245 = 5 × 7 × 7; 385 = 5 × 7 × 11

175, 245 மற்றும் 385இன் மீ.பெ.கா = 5 × 7 = 35

ஒவ்வொரு பெட்டியிலும் சம எண்ணிக்கையில் நூல்கள் உள்ளதால் தேவைப்படும் அதிகபட்சப் பெட்டிகளின் எண்ணிக்கை = 35

ஒவ்வொரு பெட்டியிலும் உள்ள ஆங்கில நூல்களின் எண்ணிக்கை = 175 ÷ 35 = 5 

ஒவ்வொரு பெட்டியிலும் உள்ள அறிவியல் நூல்களின் எண்ணிக்கை = 245 ÷ 35 = 7

ஒவ்வொரு பெட்டியிலும் உள்ள கணித நூல்களின் எண்ணிக்கை = 385 ÷ 35 = 11

ஆகவே, பெட்டியிலுள்ள நூல்களின் மொத்த எண்ணிக்கை = 5 + 7 + 11 = 23.

குறிப்பு

● மீ.சி.ம ஆனது எப்பொழுதும் கொடுக்கப்பட்ட எண்களில் பெரிய எண்ணை விடப் பெரியதாகவோ அல்லது சமமாகவோ இருக்கும்.

● மீ.சி.ம ஆனது எப்போதும் மீ.பெ.கா–வின் மடங்காக இருக்கும்.

எடுத்துக்காட்டு 8:

18 மற்றும் 30 ஆகிய எண்களின் மீ.பெ.கா மற்றும் மீ.சி.ம–வின் விகிதத்தைக் காண்க.

தீர்வு:

18 = 2 × 3 × 3 மற்றும் 30 = 2 × 3 × 5

இதன் மீ.பெ.கா = 2 × 3 = 6

மீ.சி.ம = 2 × 3 × 3 × 5 = 90

ஆகவே, மீ.பெ.கா மற்றும் மீ.சி.ம–வின் விகிதம் = 6 : 90 = 1:15

எடுத்துக்காட்டு 9:

254 மற்றும் 508 ஆகிய எண்களால் வகுக்கும் போது மீதியாக 4–ஐத் தரும் மிகச்சிறிய எண்ணைக் காண்க

தீர்வு :

254 மற்றும் 508 இன் எல்லாப் பொது மடங்குகளும் இவ்விரு எண்களால் வகுபடும்.

நாம், வகுத்தல் முறையில் 254 மற்றும் 508 ஆகிய எண்களின் மீ.சி.ம–வைக் காணலாம்.

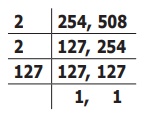
254 மற்றும் 508 இன் மீ.சி.ம = 2 × 2 × 127 = 508

ஆகவே, 508 ஆனது, 254 மற்றும் 508 ஆகிய எண்களால் வகுபடும் மிகச்சிறிய பொது மடங்கு ஆகும். இப்பொழுது, 254 மற்றும் 508 ஆல் வகுக்கும் போது நமக்கு மீதி 4 தேவை என்பதால், தேவையான எண் மீ.சி.ம–வைக் காட்டிலும் 4 அதிகம். ஆகவே, தேவையான எண் 508 + 4 = 512 ஆகும்.

எடுத்துக்காட்டு 10:

72 மற்றும் 108 ஆகிய எண்களால் சரியாக வகுபடக்கூடிய மிகச்சிறிய 5 இலக்க எண் என்ன?

தீர்வு:

முதலில், நாம் வகுத்தல் முறையில் 72 மற்றும் 108 ஆகிய எண்களின் மீ.சி.ம–வைக் காண்போம்.

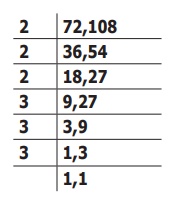
72 மற்றும் 108 இன் மீ.சி.ம = 2 × 2 × 2 × 3 × 3 × 3 = 216  

இப்போது, 216 இன் எல்லா மடங்குகளும் 72 மற்றும் 108 ஆகிய எண்களால் சரியாக வகுபடும்.

மிகச்சிறிய ஐந்திலக்க எண் = 10000 ஆகும்.

10000–ஐ 216 ஆல் வகுத்தால் ஈவு 46 மற்றும் மீதி 64. எனவே, 216 இன் அடுத்த மடங்கான, 216 × 47 = 10152 என்பது 72 மற்றும் 108 ஆல் சரியாக வகுபடக் கூடிய மிகச்சிறிய 5 இலக்க எண் ஆகும்.

எடுத்துக்காட்டு 11:

ஒரு வீட்டில் நான்கு அலைபேசிகள் உள்ளன. காலை 5 மணிக்கு, எல்லா அலைபேசிகளும் ஒன்றாக ஒலிக்கும். அதன் பின், முதல் அலைபேசியானது ஒவ்வொரு 15 நிமிடங்களிலும் இரண்டாவது அலைபேசியானது ஒவ்வொரு 20 நிமிடங்களிலும் மூன்றாவது அலைபேசியானது ஒவ்வொரு 25 நிமிடங்களிலும் மற்றும் நான்காவது அலைபேசியானது ஒவ்வொரு 30 நிமிடங்களிலும் ஒலிக்கின்றன எனில், அவை மீண்டும் எப்போது ஒன்றாக ஒலிக்கும்?

தீர்வு:

இது மீ.சி.ம தொடர்பான கணக்கு ஆகும். ஆகவே, நாம் 15, 20, 25 மற்றும் 30 ஆகிய எண்களின் மீ.சி.ம–வைக் காண வேண்டும்.

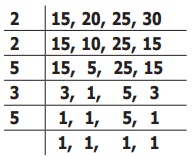
15, 20, 25 மற்றும் 30 இன் மீ.சி.ம = 2 × 2 × 3 × 5 × 5

= 300 நிமிடங்கள்

= 5 × 60 நிமிடங்கள்

= 5 × 1 மணி நேரம்

= 5 மணி நேரம்

எனவே, நான்கு அலைபேசிகளும் மீண்டும் காலை 10 மணிக்கு ஒன்றாக ஒலிக்கும்.

இவற்றை முயல்க

ஒரு சிறுவன் கூடையிலுள்ள விளாம்பழங்களை விற்பதற்காக ஒரு பட்டணத்துக்கு எடுத்துச் சென்றான். கொண்டு செல்லும் வழியில் வழிப்பறிக் கொள்ளையர்கள் சிறுவனிடம் இருந்த பழங்களைக் கொள்ளையடித்துத் தின்று விட்டார்கள். அச்சிறுவன் அரசனிடம் முறையிட, அரசன் "நீ கொண்டு வந்த பழங்கள் எத்தனை?" என்று கேட்டார். "எனக்குத் தெரியாது. ஆனால் நான் கொண்டு வந்த பழங்களை இரண்டிரண்டாகப் பிரித்தால், ஒரு பழம் மிஞ்சும். மூன்று மூன்றாகப் பிரித்தால், இரண்டு பழங்கள் மிஞ்சும். நான்கு நான்காகப் பிரித்தால், மூன்று பழங்கள் மிஞ்சும். ஐந்து ஐந்தாகப் பிரித்தால், நான்கு பழங்கள் மிஞ்சும். ஆறு ஆறாகப் பிரித்தால், ஐந்து பழங்கள் மிஞ்சும். ஏழு ஏழாகப் பிரித்தால், மீதி ஏதும் இருக்காது" எனக் கூறினான் எனில், அச்சிறுவன் கொண்டு வந்த விளாம்பழங்கள் எத்தனை? (இந்தக் கணக்கு, "விளாம்பழக் கணக்கு" என்ற தலைப்பில், கணக்குகளின் தமிழ்த் தொகுப்பு நூலான "கணக்கதிகாரம்" என்ற நூலிலிருந்து எடுக்கப்பட்டது).

தீர்வு :

சிறுவனிடமிருந்த மொத்த பழங்கள் 2, 3, 4, 5 மற்றும் 6 ஆல் வகுக்கும்போது முறையே 1, 2, 3, 4 மற்றும் 5 ஐ மீதமாகத் தருகின்றன. 

இங்கு (2 – 1) = (3 – 2) = (4 – 3) = (5 –  4) = (6 – 5) = 1 

ஃ மொத்த பழங்கள் = மீ.சி.ம. (2, 3, 4, 5, 6) – 1.

ஃ மீ.சி.ம (2, 3, 4, 5, 6) = 2 × 3 × 2 × 5 = 60 

ஃ சிறுவனிடமிருந்த மொத்த பழங்கள் 7 ஆல் வகுக்கும்போது மீதம் இருக்கக்கூடாது. எனவே தேவையான எண் 60 இன் மடங்கு 120 – 1 = 119

சிறுவனிடம் 119 பழங்கள் இருந்தன.