காஸ் விதியின் பயன்பாடுகள்

காஸ் விதியின் பயன்பாடுகள்

ஏதேனும் ஒரு வடிவமுள்ள மின் துகள் தொகுதிகளுக்கு மின்புலத்தைக் கணக்கிட கூலூம் விதி அல்லது காஸ் விதியைப் பயன்படுத்தலாம். மின்துகள் அமைப்பு ஏதேனுமொரு சமச்சீர் தன்மையைப் பெற்றிருந்தால் மின்புலத்தைக் கணக்கிட காஸ் விதியே மிகச்சிறந்த வழியாகும். பின்வரும் நேர்வுகளில் இதைக் காணலாம்.

(i) மின்னூட்டம் பெற்ற முடிவிலா நீளம் உடைய கம்பியினால் ஏற்படும் மின்புலம்

λ எனும் சீரான மின்னூட்ட நீள் அடர்த்தி (ஓரலகு நீளத்திற்கான மின்னூட்ட மதிப்பு) கொண்ட முடிவிலா நீளமுடைய கம்பியைக் கருதுவோம். கம்பியிலிருந்து r செங்குத்துத் தொலைவில் புள்ளி P உள்ளது. [படம் 1.36 (அ)]. காஸ் விதியைப் பயன்படுத்தி P இல் உருவாகும் மின்புலத்தைக் கணக்கிடலாம்.

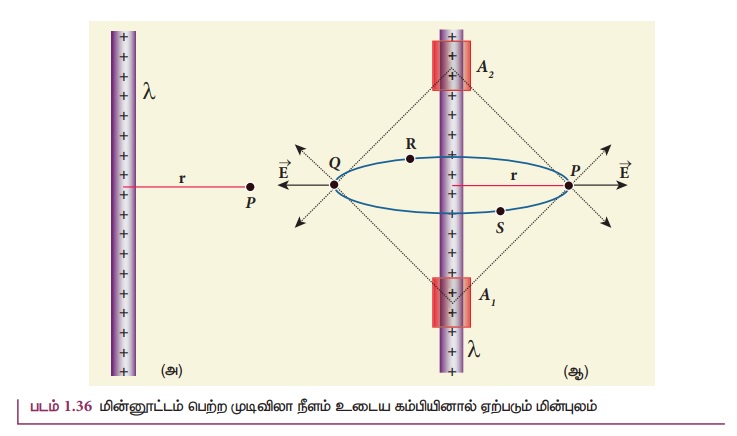
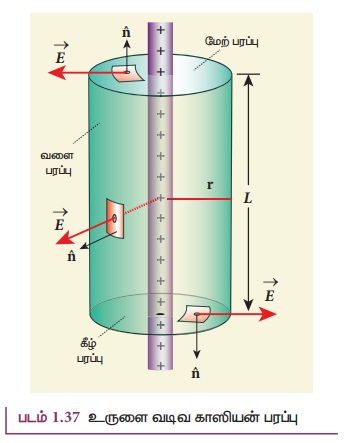
புள்ளி P இலிருந்து சம தொலைவில், கம்பியில் அமைந்துள்ள இரு சிறிய மின்துகள் கூறுகளை எடுத்துக்கொள்வோம் (படம் 1.36 (ஆ)) இவ்விரு மின் துகள் கூறுகளினால் உருவாகும் தொகுபயன் மின்புலமானது மின்னூட்டம் பெற்ற கம்பியிலிருந்து ஆர வழியே வெளிநோக்கிய திசையில் அமைகின்றது. மேலும், r ஆரமுடைய வட்டத்தின் அனைத்துப் புள்ளிகளிலும் அதன் எண்மதிப்பு சமமாக இருக்கும். இது படம் 1.36 (ஆ ) வில் காட்டப்பட்டுள்ளது. இந்தப் பண்பின் அடிப்படையில் மின்னூட்டம் பெற்ற கம்பி உருளை வடிவ சமச்சீர் தன்மை உடையது எனலாம். எனவே r ஆரமும் L நீளமும் கொண்ட உருளை வடிவ காஸியன் பரப்பைக் கருதுவோம். [படம் 1.37]

இப்பரப்பிற்கான மொத்த மின்பாயத்தை பின்வருமாறு கணக்கிடலாம்.

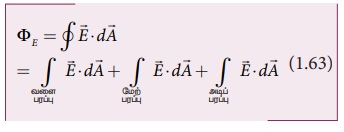
வளைப்பரப்பில்  ஆனது  க்கு இணையாக உள்ளதால் (பார்க்க படம் 1.37),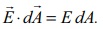 

மேல் மற்றும் அடிப்பரப்புகளுக்கு  ஆனது விற்கு செங்குத்தாக உள்ளதால், 

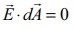
இம்மதிப்புகளை சமன்பாடு (1.63)ல் பிரதியிட்டு காஸ் விதியை உருளை வடிவ பரப்பிற்குப் பயன்படுத்தினால்

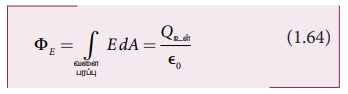
மொத்த வளை பரப்பைப் பொருத்தவரை மின்புலத்தின் எண் மதிப்பு மாறிலியாக உள்ளதால், E ஆனது தொகையிடல் குறியீட்டுக்கு வெளியே எடுக்கப்படுகிறது. மேலும் Q_உள் = λL எனப் பிரதியிட,

இங்கு 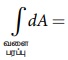 = வளைபரப்பின் மொத்த பரப்பு =  2 πrL

இதை சமன்பாடு (1.65) ல் பிரதியிட,

புள்ளி மின்துகள் ஒன்றின் மின்புலம் 1/ r² என்றவாறு இருப்பதை அறிவோம். மாறாக மின்னூட்டம் பெற்ற முடிவிலா நீளமுடைய கம்பியின் மின்புலம் 1/r என்றவாறு அமைந்துள்ளது.

கம்பிக்கு செங்குத்தான திசையிலேயே (r^) மின்புலம் எப்போதும் அமைந்துள்ளது என்பதை சமன்பாடு (1.67) மூலம் அறிய முடிகிறது. மேலும் λ> 0 எனில், கம்பிக்கு செங்குத்தாக வெளிநோக்கிய திசையில் இருக்கும்; λ< 0 எனில், உள்நோக்கிய திசையில் (-r^) செங்குத்தாக  இருக்கும்.

முடிவிலா நீளமுள்ள மின்னூட்டம் பெற்ற கம்பிக்கு மட்டுமே சமன்பாடு (1.67) பொருந்தும். வரம்பிற்குட்பட்ட நீளமுள்ள மின்னூட்டம் பெற்ற கம்பியைப் பொருத்தவரை மின்புலமானது அனைத்து புள்ளிகளிலும் ஆரத்திசையில் அமைவதில்லை. இருப்பினும், அத்தகைய கம்பியின் மையப்புள்ளிக்கு அருகிலும் கம்பியின் முனைகளிலிருந்து வெகு தொலைவிலுமுள்ள புள்ளிகளுக்கும் சமன்பாடு (1.67) ஐப் பயன்படுத்தலாம்.

(ii) மின்னூட்டம் பெற்ற முடிவிலா சமதளத் தட்டினால் உருவாகும் மின்புலம்

எனும் சீரான மின்னூட்டப் பரப்படர்த்தி (ஓரலகு பரப்பிற்கான மின்னூட்ட மதிப்பு) கொண்ட முடிவிலா சமதளத்தட்டு ஒன்றைக் கருதுவோம். அத்தட்டிலிருந்து r தொலைவில் P என்ற புள்ளி உள்ள து [படம் 1.38].

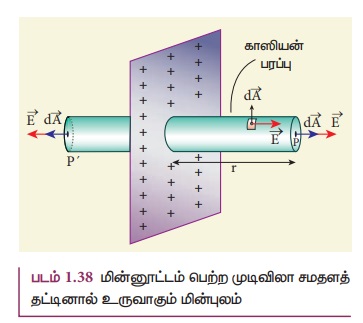
சமதளத்தின் அளவு முடிவிலாதது என்பதால், அதிலிருந்து சம தொலைவில் உள்ள அனைத்து புள்ளிகளிலும் மின்புலத்தின் மதிப்பு சமமாக இருக்கும். அனைத்து புள்ளிகளிலும் மின்புலத்தின் திசை ஆர வழியே அமைந்திருக்கும். 2r நீளமும் A குறுக்குவெட்டுப் பரப்பு கொண்ட உருளை வடிவ காஸியன் பரப்பைக் கருதுவோம்; அதன் நடுப்பகுதி வழியாக முடிவிலா சமதளத்தட்டு கடப்பதாகக் கொள்வோம். இவ்வுருளை வடிவ பரப்புக்கு காஸ் விதியைப் பயன்படுத்தினால்

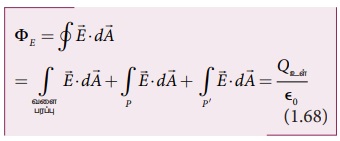
வளைபரப்பின் மேலுள்ள அனைத்து புள்ளிகளிலும் மின்புலமானது பரப்பளவுக் கூறுகளுக்கு செங்குத்தாகவும் P மற்றும் P' பரப்புகளில் அது இணையாகவும் இருக்கிறது (படம் 1.38). எனவே

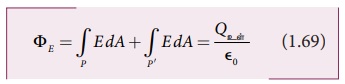
இவ்விரு பரப்புகளுக்கும் மின்புலத்தின் எண் மதிப்பு சீராக உள்ளதால் தொகையிடல் குறியீட்டுக்கு வெளியே E எடுக்கப்படுகிறது. மேலும் Q_உள், = A. எனவே

P அல்லது P’ பரப்பின் மொத்த பரப்பளவு

இங்கு n^ என்பது சமதளத்திற்கு செங்குத்தாக, வெளிநோக்கிய திசையிலுள்ள ஓரலகு வெக்டராகும். மின்னூட்டம் பெற்ற முடிவிலா சமதளத்தட்டினால் உருவாகும் மின்புலமானது மின்னூட்ட பரப்படர்த்தியைத் சார்ந்தும் அதே சமயம் தொலைவைச் சாராமலும் இருக்கின்றது.

மின்னூட்டம் பெற்றத் தட்டிலிருந்து கணிசமான தொலைவிலுள்ள எந்தவொரு புள்ளியிலும் மின்புலம் சமமாக இருக்கும். > 0 எனில் எந்தவொரு புள்ளியிலும் (P) மின்புலமானது (தட்டின்) தளத்திற்கு செங்குத்தாக, வெளிநோக்கிய திசையிலும் (n^) < 0 எனில் மின்புலமானது தளத்திற்கு செங்குத்தாக உள்நோக்கிய திசையிலும் (-n^) இருக்கும் என்பதை சமன்பாடு (1.71) மூலம் அறியலாம்.

வரம்பிற்குட்பட்ட பரப்பளவைக் கொண்ட மின்னூட்டம் பெற்ற சமதளத் தட்டைப் பொருத்தவரை தட்டின் நடுப்பகுதியில் சமன்பாடு (1.71) ஓரளவு பொருந்தும். மேலும் அதன் முனைகளிலிருந்து வெகு தொலைவிலுள்ள புள்ளிகளுக்கும் இச்சமன்பாடு பொருந்தும்.

(iii) மின்னூட்டம் பெற்ற இரு இணையான முடிவிலாதட்டுகளினால் உருவாகும் மின்புலம்

+ மற்றும் - என்கிற மின்னூட்டப் பரப்படர்த்தி கொண்ட இரு முடிவிலா மின்னூட்டம் பெற்ற

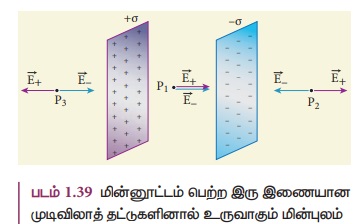
சமதள தட்டுகளைக் கருதுவோம். படம் (1.39) இல் காட்டியபடி அவை ஒன்றுக்கொன்று இணையாக உள்ளன.

தட்டுகளுக்கு இடையேயும், தட்டுகளுக்கு வெளியிலும் உருவாகும் மின்புலத்தை காஸ் விதியைப் பயன்படுத்தி கண்டுபிடிக்கலாம். மின்னூட்டம் பெற்றமுடிவிலா சமதளத் தட்டின் மின்புல மதிப்பு 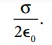மேலும் > 0 எனில் அது செங்குத்தாக, வெளிநோக்கிய திசையிலும். < 0 எனில் அது (செங்குத்தாக) உள்நோக்கிய திசையிலும் இருக்கும்.

P₂ மற்றும் P₃ ஆகிய புள்ளிகளில் இரு தட்டுகளினால் ஏற்படும் மின்புலங்களின் எண் மதிப்பு சமமாகவும் எதிரெதிர் திசை உடையதாகவும் உள்ளன. [படம் 1.39]. எனவே, தட்டுகளுக்கு வெளியே உள்ள புள்ளிகளில் மின்புலம் சுழியாகும். ஆனால் தட்டுகளுக்கு இடையே உள்ள புள்ளிகளில் (P₁) அவற்றின் மின்புலங்கள் ஒரே திசையில், அதாவது வலது திசை நோக்கி அமைவதால்,

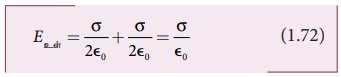
தட்டுகளுக்கு இடையே மின்புலமானது நேர் மின்னூட்டம் பெற்றத் தட்டிலிருந்து எதிர்மின்னூட்டம் பெற்றத் தட்டை நோக்கிய திசையிலிருக்கும். மேலும் தட்டுகளுக்கு இடையில் உள்ள அனைத்துப் புள்ளிகளிலும் மின்புலம் சீராக இருக்கும்.

(iv) மின்னூட்டம் பெற்ற உள்ளீடற்ற கோளத்தினால் உருவாகும் மின்புலம்

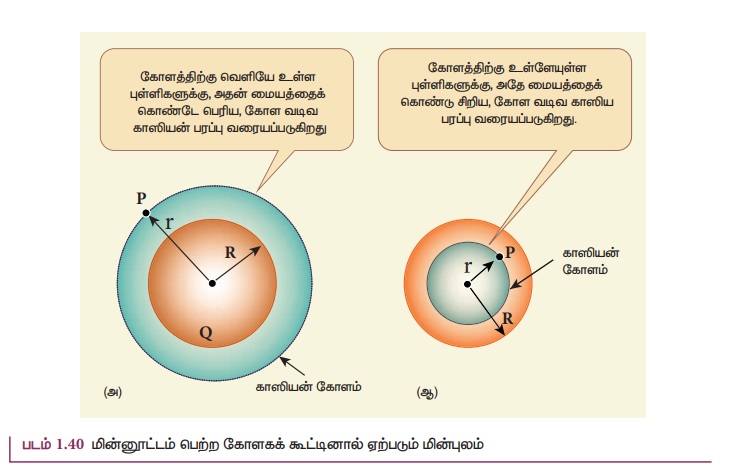
R ஆரமும் Q மின்னூட்டமும் கொண்ட, சீரான மின்துகள் பரவல் பெற்ற உள்ளீடற்ற கோளம் ஒன்றைக் கருதுவோம் (படம் 1.40). காஸ் விதியைப் பயன்படுத்தி கோளத்திற்கு வெளியேயும் உள்ளேயும் உள்ள புள்ளிகளில் மின்புலத்தைக் கணக்கிடலாம்.

நேர்வு (அ) கோளத்திற்கு வெளியில் உள்ள புள்ளியில் (r > R)

படம் 1.40 (அ) வில் காட்டியுள்ளவாறு, கோளத்தின் மையத்திலிருந்து r தொலைவில், கோளத்தின் வெளியே உள்ள புள்ளி P ஐக் கருதுவோம். மின்துகள்கள் கோளத்தின் புறப்பரப்பில் சீராகப் பரவியுள்ளன (கோளகச் சமச்சீர் தன்மை). ஆகவே Q> 0 எனில் மின்புலம் ஆர வழியே வெளிநோக்கிய திசையிலும் Q<0 எனில் ஆர வழியே உள்நோக்கிய திசையிலும் இருக்கிறது. r ஆரம் கொண்ட கோள வடிவ காஸியன் பரப்பினைக் கருதுவோம். இப்பரப்பினால் சூழப்படும் மின் துகள்களின் மொத்த மின்னூட்டம் Q என்க. காஸ் விதியைப் பயன்படுத்தி

காஸியன் பரப்பின் அனைத்து புள்ளிகளிலும் மின்புலமும்() பரப்பளவுக்கூறும்  ஒரே திசையில் (வெளிநோக்கிய திசையில், செங்குத்தாக) அமைகின்றன. மின்துகள் நிலையமைப்பின் கோளகச் சமச்சீர் தன்மையால் காஸியன்பரப்பில் உள்ள அனைத்து புள்ளிகளிலும் ன் எண்மதிப்பும் சமமாகவே இருக்கும்.

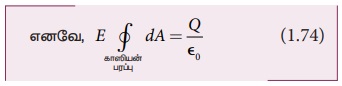
ஆனால் காஸியன் பரப்பின் மொத்த பரப்பளவு4 πr² இதை சமன்பாடு (1.74) இல் பிரதியிட ,

வெக்டர் வடிவில்,

Q > 0 எனில் மின்புலமானது ஆர வழியே வெளிநோக்கிய திசையிலும், Q < 0 எனில் ஆரவழியே உள்நோக்கிய திசையிலும் அமையும். கோளத்திற்கு வெளியே உள்ள புள்ளிகளைப் பொருத்த வரை, உள்ளீடற்ற கோளத்தின் மையத்தில் Q மின்னூட்டம் கொண்ட ஒரு புள்ளி மின்துகளை வைத்தால் எவ்வாறு மின்புலம் அமையுமோ அவ்வாறு கோளத்தின் மின்புலமானது அமைகிறது (ஈர்ப்பியலில் இதே போன்றதொரு முடிவை, M நிறை கொண்ட உள்ளீடற்ற கோளத்தினால் ஏற்படும் ஈர்ப்பு விசையைத் தருவிக்கும் போது பெற்றதை நினைவில் கொள்ளவும்)

நேர்வு (ஆ): கோளத்தின் புறப்பரப்பில் உள்ள புள்ளியில் (r = R)

கோளகக் கூட்டின் புறப்பரப்பில் உள்ள புள்ளிகளுக்கு (r = R) மின்புலமானது

நேர்வு (இ): கோளத்திற்கு உள்ளேயுள்ள புள்ளியில் (r<R)

கோளகத்தின் மையத்திலிருந்து r தொலைவில், கோளத்திற்கு உள்ளேயுள்ள புள்ளி P ஐக் கருதுவோம்.r ஆரம் கொண்ட கோள வடிவ காஸியன் பரப்பு ஒன்றை வரைவோம் (படம் 1.40 (ஆ))

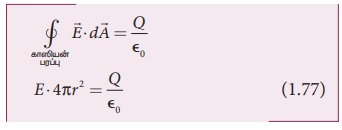
இந்த காஸியன் பரப்புக்குள்ளே எந்த ஒரு மின்துகளும் இல்லாததால் Q = 0. எனவே, சமன்பாடு (1.77)-ன் படி

மேற்பரப்பின் மீது மின் துகள்கள் சீராக பரவப் பெற்ற உள்ளீடற்ற கோளத்தின் உள்ளே அமைந்துள்ள அனைத்து புள்ளிகளுக்கும் மின்புலம் சுழியே. ஆரத்தொலைவுக்கும் (radial distance) மின்துகள்கள் சீரான பரவல் பெற்ற உள்ளீடற்ற கோளத்தின் மின்புலத்திற்கும் இடையேயான வரைபடம் படம் 1.41-ல் காட்டப்பட்டுள்ளது.

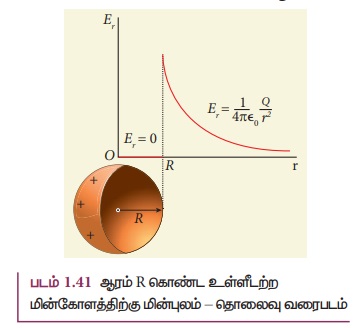
குறிப்பிட்டவொருமின்துகள் நிலையமைப்பானது கோளக, உருளை அல்லது சமதள சமச்சீர் தன்மை கொண்டிருக்கும் போது அத்தகையமின்துகள் அமைப்புகளின் மின்புலத்தை எளிதில் கண்டறிய காஸ் விதி ஒரு சிறந்த வழிமுறையாகும். அத்தகைய சமச்சீர் தன்மை அமையாத நிலையில் நேரடியான வழிமுறையையே (கூலூம் விதியும் நுண்கணிதமும்) பின்பற்ற வேண்டும். எடுத்துக்காட்டாக, மின் இருமுனையின் மின்புலத்தைக் கண்டறிய காஸ் விதியைப் பயன்படுத்துவது கடினம். ஏனெனில், அதற்கு மேலே குறிப்பிட்ட எந்தவொரு சமச்சீர் தன்மையும் கிடையாது.