நடைபாதையின் பரப்பளவு (Area of Pathways)

நடைபாதையின் பரப்பளவு (Area of Pathways)

நடைபாதைகள் பல்வேறு வடிவங்களில் இருப்பதைக் காண்கிறோம். இங்கு, வட்ட நடைபாதை, செவ்வக நடைபாதை ஆகிய இரு வகைகள் குறித்துக் காண்போம்.. 

1. வட்டப்பாதை (Circular Pathways)

நம்மைச் சுற்றியுள்ள வட்ட வடிவங்களை உற்று நோக்கினால், அங்கு வட்ட நடைபாதை இருப்பதைக் காணலாம். வட்ட நடைபாதை என்பது வெளி வட்டத்திற்கும் உள் வட்டத்திற்கும் இடைப்பட்ட பரப்பளவாகும். வெளி வட்டத்தின் ஆரம் ‘R' எனவும், உள் வட்டத்தின் ஆரம் 'r' எனவும் கருதுவோம்.

ஆகவே, வட்ட நடைபாதையின் பரப்பளவு = πR2 – πr2

= π (R2 – r2) ச. அலகுகள்.

2. செவ்வகப்பாதை (Rectangular Pathways)

படம் 2.23-ல் உள்ளது போல், ஒரு செவ்வக வடிவப் பூங்காவைக் கருத்தில் கொள்க. அந்தப் பூங்காவின் வெளிப்புறத்தில் ஒரு சீரான பாதை அமைக்கப்பட்டால், அந்தப் பாதையின் பரப்பளவை எவ்வாறு கணக்கிடுவது?

அந்தப் பூங்காவை உள்ளடக்கிய சீரான பாதையும் செவ்வக வடிவில் உள்ளது. பூங்காவுடன் கூடிய பாதையை வெளிப்புறச் செவ்வகமாகக் கருதினால், பூங்கா உட்புறச் செவ்வகம் ஆகும். பூங்காவின் நீள, அகலம் l, b என்க. எனவே உட்புறச் செவ்வகத்தின் பரப்பளவு = lb ச. அலகுகள் ஆகும்.

w என்பது பாதையின் சீரான அகலம் என்க. எனவே, வெளிப்புறச் செவ்வகத்தின் நீள, அகலம் L மற்றும் B எனில், L =1+2w , B = b +2w.

இங்கு, செவ்வக நடைபாதையின் பரப்பளவு

= வெளிப்புறச் செவ்வகத்தின் பரப்பளவு - உட்புறச் செவ்வகத்தின் பரப்பளவு

= (LB - lb) ச.அலகுகள்

எடுத்துக்காட்டு 2.15 

ஒரு பூங்கா வட்ட வடிவில் உள்ளது. அதன் மையப்பகுதியில், குழந்தைகளுக்கான விளையாட்டுப் பகுதியும், அதனைச் சுற்றி வட்ட வடிவ நடைப் பயிற்சிப் பாதையும் அமைந்துள்ளது. அந்தப் பூங்காவின் வெளிவட்ட ஆரம் 10 மீ மற்றும் உள் வட்ட ஆரம் 3 மீ எனில், நடைப்பயிற்சிப் பாதையின் பரப்பளவு காண்க.  

தீர்வு 

வெளி வட்டத்தின் ஆரம் R =10 மீ

    உள் வட்டத்தின் ஆரம் r = 3 மீ

வட்ட நடைபாதையின் பரப்பளவு = வெளிவட்டப் பரப்பளவு - உள்வட்டப் பரப்பளவு

= πR2 – πr2 

= π(R2 – r2) ச. அலகுகள் 

= 22/7 × (102 -32) 

= 22/7 × (10 × 10 - 3×3) 

= 22/7 × (100 - 9)

= 22/7 × 91

= 286 மீ2

இவற்றை முயல்க 

(i) ஒரு வட்டப்பாதையின் வெளி மற்றும் உள் ஆரங்கள் 9 செ.மீ மற்றும் 6 செ.மீ எனில், அதன் அகலம் காண்க. 

வட்டத்தின் வெளி ஆரம் R = 9 செ.மீ

உள் ஆரம் r = 6 செ.மீ

பாதையின் அகலம்  w = R – r

 = 9 – 6 = 3 cm.

(ii) ஒரு வட்டப்பாதையின் பரப்பளவு 352 ச.செ.மீ மற்றும் அதன் வெளி ஆரம் 16 செ.மீ எனில், அதன் உள் ஆரம் காண்க. 

பாதையின் பரப்பளவு = π (R2 – r2) = 352 சதுர செ.மீ

வெளிப்புற ஆரம் R = 16 செ.மீ

22/7 (162 – r2) = 352

 256 – r2 = 352 / 22 ⊂ 7 = 112

– r2 = 112 – 256 = – 144

r2 = 144 = 122

r = 12 செ.மீ

உள் ஆரம் = 12 செ.மீ

(iii) உட்புறச் செவ்வகத்தின் பரப்பளவு 15 ச.செ.மீ மற்றும் வெளிப்புறச் செவ்வகத்தின் பரப்பளவு 48 ச.செ.மீ எனில் செவ்வக நடைபாதையின் பரப்பளவு காண்க.

வெளிப்புற செவ்வகத்தின் பரப்பளவு  πR2 = 48  சதுர செ.மீ

உட்புற  செவ்வகத்தின் பரப்பளவு πr2 =15  சதுர செ.மீ

செவ்வக பாதையின் பரப்பளவு  = πR2 – πr2

 = (48–15)  சதுர செ.மீ

 = 33  சதுர செ.மீ

எடுத்துக்காட்டு 2.16 

ஒரு வட்ட வடிவப் பூந்தோட்டத்தின் ஆரம் 21 மீ. அந்தத் தோட்டத்தைச் சுற்றி, 14 மீ அகலம் உள்ள வட்ட நடைபாதை உள்ளது எனில், அந்த வட்டப்பாதையின் பரப்பளவு காண்க.

தீர்வு

உள்வட்டத்தின் ஆரம் r = 21 மீ 

உள்வட்டத்தைச் சுற்றி நடைபாதை உள்ளது. 

எனவே, வெளிவட்டத்தின் ஆரம் R = r + w

R = 21+14 = 35 மீ 

வட்ட நடைபாதையின் பரப்பளவு    = π (R2 –r2) ச.அலகுகள்

 = 22/7 × (352 - 212 ) 

 = 22/7 × ((35×35)-(21×21))

= 22/7 × (1225-441)

= 22/7 × 784

= 22 × 112 = 2644 மீ2

எடுத்துக்காட்டு 2.17    

வட்ட வடிவ மட்டைப் பந்துத் (cricket) திடலின் ஆரம் 76 மீ. அந்தத் திடலைச் சுற்றிலும் 2 மீ அகலத்தில் மழைநீர் வடிவதற்கான வடிகால் (drainage) அமைக்க வேண்டியிருந்தது. ஒரு சதுர மீட்டருக்கு ₹ 180 வீதம் செலவானால், அந்த வடிகால் அமைக்கத் தேவையான மொத்தத் தொகையைக் காண்க.

தீர்வு

(திடலின்) உள்வட்ட ஆரம்   r = 76 மீ 

விளையாட்டுத் திடலைச் சுற்றி மழைநீர் வடிகால் அமைக்கப்படுகிறது.

எனவே, வெளிவட்ட ஆரம் R = 76+2 = 78 மீ 

வட்டப்பாதையின் பரப்பளவு = π (R2 –r2) ச.அலகுகள்

= 22/7 × (782 -  762)

= 22/7 × (6084 – 5776)

= 22/7 × 308

= 22 × 44 = 968 மீ2

வடிகால் அமைக்க, ஒரு சதுர மீட்டருக்கு ₹180.

ஆகவே, மொத்தச் செலவு = 968 × 180= ₹1,74,240.

எடுத்துக்காட்டு 2.18 

ஒரு தளம் 10 மீ நீளமும், 8 மீ அகலமும் உள்ளது. அதன் மீது 7 மீ நீளமும், 5மீ அகலமும் உள்ள விரிப்பு விரிக்கப்பட்டுள்ளது. அந்த விரிப்பால் மூடப்படாத பகுதியின் பரப்பளவைக் காண்க.

தீர்வு 

இங்கு L =10 மீ B = 8 மீ 

தளத்தின் பரப்பளவு = L× B ச.அலகுகள்

= 10 × 8

= 80 மீ2

விரிப்பின் பரப்பளவு =l × b ச.அலகுகள்

 = 7×5

= 35 மீ2 

ஆகவே, விரிப்பால் மூடப்படாத பகுதியின் பரப்பளவு = 80 - 35

 = 45 மீ2

எடுத்துக்காட்டு 2.19  

23 செ.மீ நீளமும், 11 செ.மீ அகலமும் உள்ள ஓர் அட்டையில், அனைத்துப் பக்கங்களிலும் 3 செ.மீ விளிம்பு (margin) இருக்கும் வகையில் ஓர் ஓவியம் வரையப்பட்டுள்ளது. அந்த விளிம்புப் பகுதியின் பரப்பளவைக் காண்க. 

தீர்வு 

இங்கு L = 23 செ.மீ  B =11 செ.மீ 

அட்டையின் பரப்பளவு = L × B

=23×11

= 253 செ.மீ2

l =L - 2w = 23 – 2(3) = 23 – 6 = 17 செ.மீ 

b = B - 2w = 11 - 2(3) = 11 – 6 = 5 செ.மீ

ஓவியத்தின் பரப்பளவு 17 × 5 = 85 செ.மீ2 

விளிம்புப் பகுதியின் பரப்பளவு = 253 – 85

 = 168 செ.மீ2

எடுத்துக்காட்டு 2.20   

9 மீ நீளமும், 7 மீ அகலமும் உள்ள ஓர் அறைக்கு வெளியே, 3 மீ சீரான அகலமுள்ள ஒரு தாழ்வாரம் (verandah) உள்ளது. (அ) தாழ்வாரத்தின் பரப்பளவு காண்க. (ஆ) அந்தத் தாழ்வாரப் பகுதிக்கு ச.மீ-க்கு ₹15 வீதம் சிமெண்ட் பூச ஆகும் செலவைக் காண்க.

தீர்வு 

இங்கு , l = 9 செ.மீ , b = 7 செ.மீ 

அறையின் பரப்பளவு = l × b

= 9 × 7

 = 63 மீ 2

L = l + 2w = 8 + 2(3) = 8 + 6 = 14 செ.மீ 

B = b + 2w = 5 + 2(3) = 5 + 6 = 118  செ.மீ 

தாழ்வாரம் உட்பட அறையின் பரப்பளவு = L × B

= 14 ×11

= 154 மீ  2

(அ) தாழ்வாரத்தின் பரப்பளவு = தாழ்வாரம் உட்பட அறையின் பரப்பளவு - அறையின் பரப்பளவு

=154−63

= 91 மீ2

(ஆ) 1 ச.மீ-க்கு சிமெண்ட் பூச ஆகும் செலவு = ₹15

தாழ்வாரத்துக்கு சிமெண்ட் பூச ஆகும் செலவு =91 ×15= ₹1365.

எடுத்துக்காட்டு 2.21

30 மீ × 19 மீ பரிமாணங்களுடைய ஒரு கோ-கோ விளையாட்டுத் திடல், அதன் அனைத்துப் பக்கங்களிலும் லாபியியுடன் (lobby) அமைந்துள்ளது. விளையாடும் பகுதிக்கான பரிமாணங்கள் 27 மீ × 16 மீ எனில், லாபியின் பரப்பளவைக் காண்க.

தீர்வு 

கொடுக்கப்பட்ட பரிமாணங்களில் இருந்து 

L = 30 மீ;    B =19 மீ;    l = 27 மீ    b = 16 மீ 

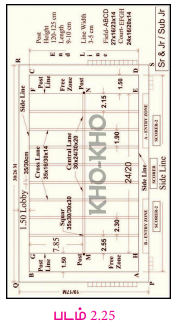
கோ-கோ திடலின் பரப்பளவு = L × B

= 30 × 19

= 570மீ2

விளையாடுவதற்கான பகுதியின் பரப்பளவு  = l × b

= 27 × 16

= 432 மீ2

லாபியின் பரப்பளவு =கோ-கோ திடலின் பரப்பளவு - விளையாடுவதற்கான பரப்பளவு

 = 570 - 432 

= 148 மீ2